13 что называют коэффициент полезного действия

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июля 2019;
проверки требуют 7 правок.
Запрос «КПД» перенаправляется сюда; см. также другие значения.
Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)[1]. КПД является безразмерной величиной и часто измеряется в процентах.
Определение[править | править код]
Математически КПД определяется как
где А — полезная работа (энергия), а Q — затраченная энергия.
Если КПД выражается в процентах, эту формулу иногда записывают в виде
.
Здесь умножение на не несёт содержательного смысла, поскольку . В связи с этим второй вариант записи формулы менее предпочтителен (одна и та же физическая величина может быть выражена в различных единицах независимо от формул, где она участвует).
В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
,
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах нагревателя T1 и холодильника T2, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен
.
Другие похожие показатели[править | править код]
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов[править | править код]
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины[править | править код]
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
Эффективность машин характеризует холодильный коэффициент[en]
,
где — тепло, отбираемое от холодного конца (в холодильных машинах холодопроизводительность); — затрачиваемая на этот процесс работа (или электроэнергия).
Для тепловых насосов используют термин коэффициент трансформации
,
где — тепло конденсации, передаваемое теплоносителю; — затрачиваемая на этот процесс работа (или электроэнергия).
В идеальной машине , отсюда для идеальной машины
Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
,
где , — температуры горячего и холодного концов, K[2]. Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент может превосходить единицу. Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр., электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.
Литература[править | править код]
- Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..
Примечания[править | править код]
Источник
Запрос «КПД» перенаправляется сюда; см. также другие значения.
Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)[1]. КПД является безразмерной величиной и часто измеряется в процентах.
Определение
Коэффициент полезного действия
Математически определение КПД может быть записано в виде:
где А — полезная работа (энергия), а Q — затраченная энергия.
Если КПД выражается в процентах, то он вычисляется по формуле:
В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.
КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле
,
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах нагревателя T1 и холодильника T2, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен
.
Другие похожие показатели
Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.
КПД котлов
КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.
Тепловые насосы и холодильные машины
Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.
Эффективность машин характеризует холодильный коэффициент (англоязычный аналог COP)
,
где — тепло, отбираемое от холодного конца (в холодильных машинах холодопроизводительность); — затрачиваемая на этот процесс работа (или электроэнергия).
Для тепловых насосов используют термин коэффициент трансформации
,
где — тепло конденсации, передаваемое теплоносителю; — затрачиваемая на этот процесс работа (или электроэнергия).
В идеальной машине , отсюда для идеальной машины
Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент
,
где , — температуры горячего и холодного концов, K[2]. Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент может превосходить единицу. Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр., электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.
Литература
- Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..
Примечания
Источник
В реальной действительности работа, совершаемая при помощи какого — либо устройства, всегда больше полезной работы, так как часть работы выполняется против сил трения, которые действуют внутри механизма и при перемещении его отдельных частей. Так, применяя подвижный блок, совершают дополнительную работу, поднимая сам блок и веревку и, преодолевая силы трения в блоке.
Введем следующие обозначения: полезную работу обозначим $A_p$, полную работу — $A_{poln}$. При этом имеем:
[A_p Определение и формула КПД
Определение
Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $eta $, тогда:
[eta =frac{A_p}{A_{poln}} left(2right).]
Чаще всего коэффициент полезного действия выражают в процентах, тогда его определением является формула:
[eta =frac{A_p}{A_{poln}}cdot 100% left(2right).]
При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.
И так, коэффициент полезного действия — это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.
Для увеличения КПД механизмов можно пытаться уменьшать трение в их осях, их массу. Если трением можно пренебречь, масса механизма существенно меньше, чем масса, например, груза, который поднимает механизм, то КПД получается немного меньше единицы. Тогда произведенная работа примерно равна полезной работе:
[A_papprox A_{poln}left(3right).]
Золотое правило механики
Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.
Выразим каждую из работ в формуле (3) как произведение соответствующей силы на путь, пройденный под воздействием этой силы, тогда формулу (3) преобразуем к виду:
[F_1s_1approx F_2s_2left(4right).]
Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.
Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.
КПД при передаче энергии
Коэффициент полезного действия можно определить как отношение полезной работы к затраченной на ее выполнение энергии ($Q$):
[eta =frac{A_p}{Q}cdot 100% left(5right).]
Для вычисления коэффициента полезного действия теплового двигателя применяют следующую формулу:
[eta =frac{Q_n-Q_{ch}}{Q_n}left(6right),]
где $Q_n$ — количество теплоты, полученное от нагревателя; $Q_{ch}$ — количество теплоты переданное холодильнику.
КПД идеальной тепловой машины, которая работает по циклу Карно равно:
[eta =frac{T_n-T_{ch}}{T_n}left(7right),]
где $T_n$ — температура нагревателя; $T_{ch}$ — температура холодильника.
Примеры задач на коэффициент полезного действия
Пример 1
Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?textit{}
Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:
[A_p=mgh left(1.1right).]
Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:
[N=frac{A_{poln}}{Delta t}to A_{poln}=NDelta tleft(1.2right).]
Воспользуемся определением коэффициента полезного действия для его нахождения:
[eta =frac{A_p}{A_{poln}}cdot 100%left(1.3right).]
Формулу (1.3) преобразуем, используя выражения (1.1) и (1.2):
[eta =frac{mgh}{NDelta t}cdot 100%.]
Ответ. $eta =frac{mgh}{NDelta t}cdot 100%$
Пример 2
Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$
Решение. Коэффициент полезного действия цикла определим как:
[eta =frac{A_p}{Q}left(2.1right).]
Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).
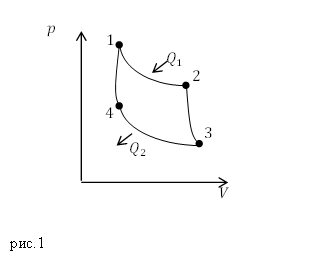
Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2.1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
[Q=Q_1=A_{12}left(2.2right).]
Газ совершает полезную работу, которую равна:
[A_p=Q_1-Q_2left(2.3right).]
Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:
[A_p=A_{12}+A_{34}left(2.4right).]
Преобразуем формулу (2.1) учитывая результаты (2.2) — (2.4):
[eta =frac{A_{12}+A_{34}}{A_{12}}to A_{12}eta =A_{12}+A_{34}to A_{34}=(eta -1)A_{12}left(2.4right).]
Так как по условию $A_{12}=A_0, $окончательно получаем:
[A_{34}=left(eta -1right)A_0.]
Ответ. $A_{34}=left(eta -1right)A_0$
Читать дальше: формула линейной скорости.
Источник
Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Определение и расшифровка КПД
Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.

Полезная работа
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
- Затрачиваемая работа Aз всегда больше полезной Ап.
- Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
- Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Источник

