Активные силы это силы полезного сопротивления
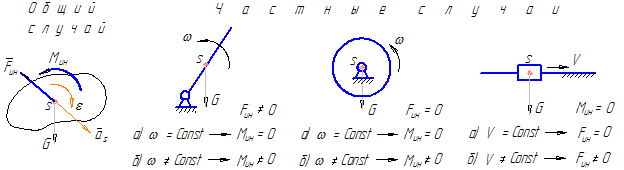

Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).
В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:
а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:
- внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;
- внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);
б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):
- движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;
- сила сопротивления препятствует движению звена и развивает отрицательную мощность.
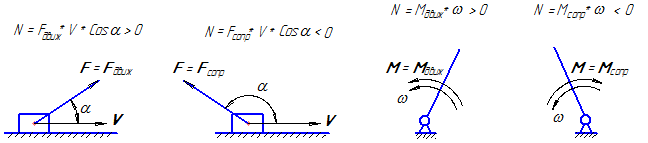
Рисунок 16
В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:
- силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);
- силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений.
Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;
в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;
г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;
д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:
Fин=-m∙as
Mин=-Is∙e
где
Fин – главный вектор сил инерции, приложенный в центре масс звена;
Mин – главный момент сил инерции;
m – масса звена;
Is – момент инерции звена относительно центра масс;
as – ускорение центра масс звена;
e – угловое ускорение звена.
Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.
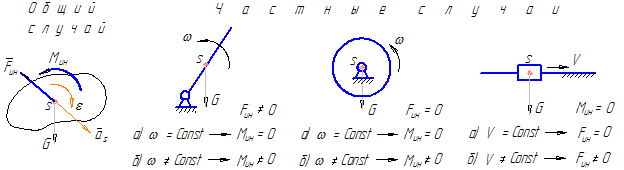
Рисунок 17
При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.
Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.
Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).
Поэтому для решения поставленной задачи применяется метод кинетостатики.
Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.
Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.
Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.
Условие статической определимости плоской кинематической цепи:
Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется «n» подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.
На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.
В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.
При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.
Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).
Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).
Если в кинематической цепи количество пар пятого класса равно Р5, то на определение реакций во всех этих парах надо затратить 2Р5 уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р4.
Таким образом, из 3n независимых уравнений статики 2Р5 уравнений используются для определения реакций в парах пятого класса и Р4 – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.
Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда
X=3n–2Р5–Р4,
но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.
Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы.
Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:
- разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;
- решение начинают с последней присоединенной группы и заканчивают начальным звеном.
При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.
Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.
Кинетостатика групп Ассура второго класса >
Курсовой проект по ТММ >
Техническая механика, теормех, сопромат, ТММ, детали машин и строймех.
Источник
При силовом расчете механизмов обычно предполагается, что заданы законы движения ведущих звеньев, хотя бы в первом приближении, и часть внешних сил.
Основными силами, определяющими характер движения механизма, являются движущие силы, совершающие положительную работу, и силы полезного (производственного) сопротивления, возникающие в процессе выполнения механизмом полезной работы и совершающие отрицательную работу. К движущим силам относятся: сила давления рабочей смеси на поршень цилиндра двигателя внутреннего сгорания, момент, развиваемый электродвигателем на ведущем валу насоса или компрессора, и т. д. Силы полезного сопротивления — это те силы, для преодоления которых предназначен механизм. Такими силами являются: силы сопротивления резанию в токарном станке, сопротивления ткани проколу иглы в швейной машине и т. д. Кроме этих сил необходимо учитывать также силы сопротивления среды, в которой движется механизм, и силы тяжести звеньев, производящие положительную или отрицательную работу в зависимости от направления движения центра тяжести звеньев — вниз или вверх. Напомним, что силой тяжести (силой веса) называют равнодействующую силы притяжения Земли и центробежной силы, возникающей при вращении тела вместе с Землей. Сила тяжести звена равна:
( ) — ускорение свободного падения.
Сила тяжести направлена вниз и прикладывается в центре тяжести звена.
Замечание: В некоторых заданиях на курсовой проект центр тяжести звеньев бывает задан. Если он не задан, то считать, что для всех звеньев (кроме кривошипа) центр тяжести находится на середине звена. Кривошип считаем однородным диском с центром тяжести, совпадающим с осью диска, т.е. сила тяжести приложена к шарниру, связывающему кривошип со стойкой.
При силовом расчете механизма в курсовом проекте силы полезного сопротивления должны быть заданы. Эти силы обычно задаются в виде так называемых механических характеристик.
Механической характеристикой двигателя или рабочей машины называют зависимость момента, приложенного к ведомому валу двигателя или к ведущему валу рабочей машины, от одного или нескольких кинематических параметров. Механические характеристики определяют экспериментальным путем или же при помощи различных математических расчётов. Механическая характеристика технологической машины может быть также задана в виде зависимости рабочего усилия на звене, связанном с инструментом, от величины рабочего хода этого звена.
а) в)
с)
Рис.1 Пример механических характеристик сил полезного сопротивления.
а) транспортировка, в) и с) вырубание изделий.
В курсовом проекте механические характеристики даны в задании в виде диаграмм изменения рабочего усилия от перемещения ползуна механизма, связанного с инструментом (рис.1).
Для определения силы полезного сопротивления необходимо вычертить в масштабе диаграмму, заданную в задании, зависимости полезной силы сопротивления от положения ползуна (рис.2). Откладываем по оси ординат заданное максимальное значение силы сопротивления , а по оси абсцисс максимальный ход ползуна , взятый из диаграммы перемещений ползуна. Далее из диаграммы необходимо найти положение ползуна для заданного положения механизма и отложив его на диаграмме сил сопротивления найти полезную силу сопротивления для рассчитываемого положения механизма.
Так, например, определим силу полезного сопротивления в диаграмме с) (рис.1) для 4-го положения рабочего хода механизма (рис.2).
Рис. 2. Определение силы полезного сопротивления с помощью заданной диаграммы.
При выполнении кинематического анализа механизма была построена диаграмма перемещения ползуна F в зависимости от положения кривошипа. Максимальное значение по оси ординат — максимальный ход ползуна. Значение по оси ординат, соответствующее 4-му положению рабочего хода механизма .
На диаграмме сил полезных сопротивлений откладываем по оси абсцисс значение и находим значение для этого положения по оси ординат .
Сила полезного сопротивления для 4-го положения рабочего хода будет равна:
Замечание: Так как в курсовом проекте силовой анализ выполняется только в двух положениях, то допускается принимать в заданном положении рабочего хода максимальную силу полезного сопротивления, а на холостом ходу – силу полезного сопротивления равную нулю.
При работе механизма в результате действия всех приложенных к его звеньям указанных сил в кинематических парах возникают реакции, которые непосредственно не влияют на характер движения механизма, но на поверхностях элементов кинематических пар вызывают силы трения. Эти силы являются силами вредного сопротивления. На данном этапе проектирования механизма (если нет специальных указаний в задании) силами трения в силовом анализе пренебрегаем.
Реакции в кинематических парах возникают не только вследствие воздействия внешних задаваемых сил на звенья механизма, но и вследствие движения отдельных масс механизма с ускорением. Силы, возникающие в результате движения звеньев механизма с ускорением, называют силами инерции.
Основная задача кинетостатического анализа (расчета) состоит в определении реакций в кинематических парах механизмов или, иначе говоря, давлений, возникающих в местах соприкосновения элементов кинематических пар, а также в определении уравновешивающих моментов или уравновешивающих сил. Под последними обычно понимают те неизвестные и подлежащие определению силы или моменты, приложенные к ведущему звену, которые уравновешивают систему всех внешних сил и пар сил и всех сил инерции и пар сил инерции.
Если механизм имеет несколько степеней свободы, то для его равновесия необходимо столько уравновешивающих сил или пар сил, сколько имеется степеней свободы. В механизме, обладающем одной степенью свободы, уравновешивающей силой является одна сила или пара сил, приложенная к ведущему звену.
В теории механизмов и машин весьма широкое применение получил так называемый кинетостатический метод силового расчета механизмов. Этот метод, как известно из курса теоретической механики, состоит в следующем. Если к точкам несвободной системы вместе с задаваемыми силами приложить силы инерции, то совокупность этих сил уравновешивается реакциями связей. Этот прием, несмотря на свою условность, обладает тем важным для практики преимуществом, что позволяет свести решение задач динамики к решению задач статики (принцип Д’Аламбера). Это имеет место, когда поставленная задача относится к первой задаче динамики, т. е. задачи об определении сил по известному движению звеньев механизма.
Источник
Åùå îäèí òåðìèí è åùå îäíî ÿâëåíèå, ñ êîòîðûì ïñèõîëîãó ÷àñòî ïðèõîäèòñÿ ñòàëêèâàòüñÿ, è êîòîðîå, êàê ÿ çàìåòèë, äàëåêî íå âñåãäà ïîíèìàåòñÿ êàê äîëæíî, íåñìîòðÿ íà òî, ÷òî â ýòîì êîíêðåòíîì ñëó÷àå ÿâëåíèå îïèñàíî êëàññèêàìè äîñòàòî÷íî ïîäðîáíî, õîòÿ, ïðèçíàþ, íå òî, ÷òîáû î÷åíü ÷åòêî.
Ñðàçó îãîâîðþñü âî èçáåæàíèå íåäîðàçóìåíèé, ÷òî ðå÷ü èäåò íå î êëàññè÷åñêîì ïñèõîàíàëèòè÷åñêîì òåðìèíå, êîòîðûé çàíèìàåò âàæíîå ìåñòî â ïñèõîàíàëèòè÷åñêîé òåðàïèè, è ïîòîìó õîðîøî ïðîïèñàí, èçó÷åí è ðàçîáðàí â ñïåöèôè÷åñêèõ ëäÿ ïîäõîäà ïîíÿòèÿõ è ðàìêàõ, à îá îáùåì ÿâëåíèè, êîòîðîå, êàê ëåãêî âèäåòü, èìååò ìåñòî íå òîëüêî â ïñèõîàíàëèçå, õîòü è áûëî âïåðâûå îïèñàíî èìåííî â ýòîì ïîäõîäå, è ïîòîìó îáîçíà÷àåòñÿ òåì æå ñàìûì ñëîâîì.
Ñîïðîòèâëåíèå ñèòóàöèÿ, ñ êîòîðîé ïñèõîëîãó ïðèõîäèòñÿ âñòðå÷àòüñÿ äîâîëüíî ÷àñòî, è äëÿ òîãî, ÷òîáû óñïåøíî åå îáðàáîòàòü, ñëåäóåò óâåðåííî ïîíèìàòü, êàê îíà âîçíèêàåò, íà ÷åì îñíîâàíà, ïî êàêèì ìåõàíèçìàì ðàáîòàåò, è òîãäà ñòàíåò ÿñíî, ÷òî ñ íåé äåëàòü.
Íà ïåðâûé âçãëÿä êàðòèíà âûãëÿäèò ñòðàííî: ÷åëîâåê ïðèõîäèò ê ïñèõîëîãó çà ïîìîùüþ è äàæå íà÷èíàåò ýòó ïîìîùü ïîëó÷àòü, êàê âäðóã ïàðàäîêñàëüíûì ìàíåðîì ïðèíèìàåòñÿ ýòó æå ïîìîùü íåÿâíî, ïðè ôîðìàëüíîé ãîòîâíîñòè ê ïðîäîëæåíèþ, îòâåðãàòü. Ïðîïóñêàåò âèçèòû, ñåðüåçíî îïàçäûâàåò, óõîäèò â çàáàëòûâàíèå, áåññìûñëåííûå ñïîðû î ìåëî÷àõ, ýìîöèîíàëüíóþ êîíôðîíòàöèþ ñ íåïîíÿòíûìè ïîâîäàìè, èãíîðèðîâàíèå, ðàññåÿííîñòü è ïðî÷óþ íåêîíñòðóêòèâíóþ åðóíäó.
Ýòî îíî, ñîïðîòèâëåíèå.
Óâåùåâàíèÿ îêàçûâàþòñÿ ìàëîýôôåêòèâíûìè: ÷åëîâåê ìîæåò ñîãëàøàòüñÿ, èñòîâî êèâàòü, óâåðÿÿ, ÷òî îí âñå ïîíÿë, ÷òî âîò òåïåðü-òî îí âñå ñäåëàåò ïðàâèëüíî è áóäåò èçî âñåõ ñèë ñòàðàòüñÿ, íî îáåùàíèÿ îêàçûâàþòñÿ ïóñòûìè. Îí âñå ðàâíî ñàáîòèðóåò âàøè óñèëèÿ. Àæ ðóêè îïóñêàþòñÿ.
Ïå÷àëüíàÿ êàðòèíà, êîãäà â ýòèõ óñëîâèÿõ, íå ïîíèìàÿ ñóòü ÿâëåíèÿ, à, ñëåäîâàòåëüíî, è òî÷êè ïðèëîæåíèÿ óñèëèé, ïñèõîëîã ïûòàåòñÿ âçûâàòü ê îòâåòñòâåííîñòè è ñîçíàòåëüíîñòè êëèåíòà, Îí æå âñå-òàêè ïñèõîëîã, è äîëæåí áûòü äàâíî â êóðñå, ÷òî ýòî ñëàáûå è íåýôôåêòèâíûå ìåõàíèçìû, íåíàäåæíî óïðàâëÿþùèå äåéñòâèÿìè ÷åëîâåêà.
À ÷òî æå äåëàòü?
Äëÿ òîãî, ÷òîáû ïîñòðîèòü ïëàí, íàäî ïîíÿòü è ÷òî ïðîèñõîäèò, è êóäà íàäî íàïðàâèòü âíèìàíèå.
À ïðîèñõîäèò åñòåñòâåííàÿ è ïîíÿòíàÿ âåùü. Îäèí ÷åëîâåê ïðèõîäèò ê äðóãîìó çà ïîìîùüþ, à ýòîò äðóãîé ïîäëûì ìàíåðîì íà÷èíàåò äåëàòü åìó áîëüíî.
Íåò, êîíå÷íî, î÷åíü òðîãàòåëåí è ìèë äî ìèìèìèøíîñòè îáðàç ëàñêîâîãî ïñèõîëîãà, êîòîðûé ñ äîáðîé è ìóäðîé óëûáêîé ñîîáùàåò êëèåíòó êàêèå-òî âåëèêèå èñòèíû, îò êîèõ êëèåíò ïðÿìî íà ìåñòå ïðîñâåòëÿåòñÿ è óõîäèò îêðûëåííûé. Íî, íàâåðíîå, ýòî âñå æå áîëüøå èç ñòóäåí÷åñêèõ ìå÷òàíèé è îáûâàòåëüñêèõ ìèôîâ. Èçðÿäíàÿ ÷àñòü ðàáîòû ïñèõîëîãà ñâîäèòñÿ ê ðàñêîâûðèâàíèþ áîëÿ÷åê, ÷àñòüþ íîâûõ, à ÷àñòüþ è ñòàðûõ, ïðèâû÷íûõ, êîòîðûå âîîáùå íåïîíÿòíî (êëèåíòó), çà÷åì òðîãàòü, è êîòîðûå åìó èçâåñòíî, êàê áåðå÷ü è íå ïîäñòàâëÿòü ïîä ñîëíå÷íûé ñâåò.
Êëèåíò äàëåêî íå âñåãäà (åñëè íå ñêàçàòü «ïî÷òè íèêîãäà íå») ïðèõîäèò ê ïñèõîëîãó ñ ÷åòêèì è ñôîðìèðîâàííûì çàïðîñîì. ×àùå îí ïðîñòî ñòàëêèâàåòñÿ ñ íåïîíÿòíûì äèñêîìôîðòîì â êîíêðåòíîé îáëàñòè, êîòîðûé åìó âîò ñðî÷íî íàäî ëèêâèäèðîâàòü, è èñêðåííå íå ïîíèìàåò, êîé ÷åðò âû âäðóã äåðãàåòå åãî ñòðàííûìè âîïðîñàìè î ðîäñòâåííèêàõ, äàâíî óæ óìåðøèõ? Çà÷åì âû çàñòàâëÿåòå åãî âñïîìèíàòü íåïðèÿòíûå è íåóäîáíûå ñîáûòèÿ, íå èìåþùèå íèêàêîãî îòíîøåíèÿ ê çàäàííîìó âîïðîñó? Íó êàêîå âàì äåëî äî òîãî, êòî åìó áèë ìîðäó â øêîëå è êòî òèñêàë åå çà ïîïó â ðîçîâîì äåòñòâå? Âàì ÷òî, äåëàòü íå÷åãî?
Äîêòîð, ÷òî ñî ìíîé? ß âîò ñþäà òûêàþ áîëüíî, ñþäà òûêàþ áîëüíî, è ñþäà òûêàþ òîæå áîëüíî, è âîò ñþäà…
Íó-êà, íó-êà, äàéòå ïîñìîòðþ… Äà ó âàñ ïàëåö ñëîìàí!
Âîò, ÿ ïðÿìî âèæó, ÷òî âû óæå ïîíèìàåòå, î ÷åì ÿ.
Íó äà, åñëè âû ïðèõîäèòå ê âðà÷ó, ÷òîáû çàøèòü ðàíó, òî âðà÷, ñóêà òàêàÿ, õâàòàåò áîëüíóþ ðàíó ðóêàìè è âòûêàåò â íåå èãîëêó. Ëàäíî, åñëè âñÿ êóëüòóðà, êíèãè, ôèëüìû è îïûò äàþò âàì ïîíèìàíèå, ÷òî òàê îíî è äîëæíî ïðîèñõîäèòü, è âû ïðåâîçìîãàåòå ñåáÿ, íå âûðûâàåòåñü è íå óáåãàåòå îò ãàäà, êîòîðûé ïðè÷èíÿåò âàì ñòðàäàíèÿ. Íî âåäü ïñèõîëîã íå âðà÷, è ìíîãî÷èñëåííûå ôèëüìû íå èíôîðìèðóþò íàñåëåíèå î ìåòîäàõ ïñèõîòåðàïèè, ïðîïàãàíäèðóÿ íàøè ñàìîîòâåðæåííîñòü, äîáðîòó è ïðîôåññèîíàëèçì. È ëþäè æäóò, ÷òî ïñèõîëîã ïî÷èíèò âàøè ñòðàäàíèÿ âîëøåáíûì îáðàçîì, ïðèÿòíûìè áåñåäàìè î âñÿêîé åðóíäå. À òî è ïðîñòî äàñò óíèâåðñàëüíûé ñîâåò, îò êîòîðîãî ñðàçó ñòàíåò âñå ÿñíî è ëåãêî.
Àãàùÿç. Ïîä íåâèííûì ïðûùîì çà÷àñòóþ îêàçûâàþòñÿ ìíîãîëåòíèå ãíîéíèêè è íåêðîçû ñ êîðíÿìè, óõîäÿùèìè äàëåêî âãëóáü, è ïðîáëåìêà, âûãëÿäÿùàÿ âïîëíå êîíêðåòíî è îòíîñèòåëüíî íåâèííî, ïðåâðàùàåòñÿ â ðàçâîðî÷åííîå îïåðàöèîííîå ïîëå, è íàñòàåò ìîìåíò, êîãäà ÷åëîâåê ñìîòðèò íà âñå ýòî ñ óæàñîì è íåäîóìåíèåì: è çà÷åì âû âñå ýòî íàòâîðèëè? Òîëüêî ÷òî æå îíî âûãëÿäåëî ãîðàçäî ïðîùå? À ñåé÷àñ è áîëüíî, è ñòðàøíî, è òðóäíî, è âìåñòî ïðîñòîé ïðîöåäóðû îïëàòû ðàáîòû ïñèõîëîãà ïðèõîäèòñÿ ñàìîìó äåëàòü êàêèå-òî íåóäîáíûå, íåïðèâû÷íûå è íåïðèÿòíûå âåùè, ìåíÿòü ñâîþ æèçíü, âûïîëíÿòü êàêèå-òî óïðàæíåíèÿ è çàäàíèÿ, ó÷èòüñÿ ÷åìó-òî íåóäîáîâàðèìîìó, à ó÷èòüñÿ óæå ðàçó÷èëñÿ, è ñòðàøíî, è âîîáùå…
È êàê âû äóìàåòå, â ýòîé ñèòóàöèè íîðìàëüíûé ÷åëîâåê áóäåò èñïûòûâàòü ðàäîñòíîå æåëàíèå ïðèéòè ê âàì ÷åðåç íåäåëþ? Âîîáùå-òî ìîæåò áûòü äàæå ïðÿìî ñåãîäíÿ îí è áóäåò, à âîò ÷åðåç íåäåëþ çà ÷àñ äî âûõîäà èç äîìà ó íåãî ïîÿâèòñÿ ùåìÿùåå ÷óâñòâî òðåâîãè, äèñêîìôîðòà, íåïðèÿçíè, êàèå-òî íåîòëîæíûå äåëà, íåäîìîãàíèå… Íó à êàê ìîæíî èñïûòûâàòü êîìôîðò è ïðèÿçíü, ñîáèðàÿñü èäòè òóäà, ãäå âàì äåëàþò áîëüíî è ñòûäíî?
Õîðîøî, åñëè êëèåíò âåñü èç ñåáÿ îñîçíàííûé, è, êàê âçðîñëûé ÷åëîâåê, ñàìîñòîÿòåëüíî îòïðàâëÿåòñÿ â áîëüíèöó íà îïåðàöèþ, ïîëíûé ðåøèòåëüíîé ãîòîâíîñòè ïðîéòè ÷åðåç âñå ìóêè õèðóðãèè è òåðàïèè. Íî âåäü â ýòîì ñëó÷àå ó íåãî åñòü ïîíèìàíèå, ÷òî èìåííî ñ íèì ñîáèðàþòñÿ ñäåëàòü, è êàêèå ïîñëåäñòâèÿ îí ìîæåò îæèäàòü. À íåîñîçíàííîìó, ñêàæåì, ìàëåíüêîìó ðåáåíêó, íåñâåäóùåìó â ìåäèöèíå, ìîæíî äîëãî äîêàçûâàòü, ÷òî äîêòîð õîðîøèé, à áîëüíûå óêîëû è ãîðüêèå òàáëåòêè ýòî õîðîøî è òàê íàäî. Ðåáåíîê ìîæåò äàæå âàì ïîâåðèòü, íî óêîëû âñå ðàâíî íå ïîëþáèò. À ó êëèåíòà íåò (îáû÷íî) òàêîãî âíåøíåãî àâòîðèòåòíîãî ðîäèòåëÿ, êîòîðûé îáúÿñíèò âíóòðåííåìó îáèæåííîìó ðåáåíêó âñå ýòî, è íå ïðîñòî îáúÿñíèò, à äîêàæåò è óáåäèò. À õîòü áû è áûë íåò ó âíåøíåãî ðîäèòåëÿ ïîíèìàíèÿ, ÷òî òàêîå äåëàåò ïñèõîëîã. È óâåðåííîñòè ïîýòîìó òîæå íåò, è äîêàçûâàíèå ïîëüçû è áëàãà ïîýòîìó òîæå âûãëÿäèò íåóáåäèòåëüíî.
È ïîïóëÿðíàÿ äåêëàðàöèÿ, ÷òî ïñèõîëîã ñ êëèåíòîì äîëæíû ðàáîòàòü íàä âîïðîñîì êëèåíòà â ñîòðóäíè÷åñòâå, òîæå âûãëÿäèò äëÿ ýìîöèîíàëüíîé ñòîðîíû êëèåíòà äèêî: â ÷åì ñîòðóäíè÷àòü? Âîò â ýòèõ áîëüíûõ êîâûðÿíèÿõ? Äà âû ÷òî, ñ óìà ñîøëè? ×òî ÿ, âðàã ñåáå? Ìàçîõèñò? Ìíå è òàê ïëîõî, ÿ ïðèøåë, ÷òîáû âû ìíå ñäåëàëè õîðîøî, à âû…
Ïîíèìàåòå, ñîïðîòèâëåíèå èñõîäèò íå îò òîé ÷àñòè ëè÷íîñòè, êîòîðàÿ ïðèâåëà êëèåíòà ê âàì íà ïðèåì. Íà ïðèåì ïðèïåðëîñü ñîçíàíèå ëîãè÷íàÿ è ïîñëåäîâàòåëüíàÿ ñòðóêòóðà (íó, îòíîñèòåëüíî). À ïðîòåñò èñõîäèò èç ñòàðûõ, ïðÿìîëèíåéíûõ è ýìîöèîíàëüíûõ ñòðóêòóð, ðåôëåêñîâ è àâòîìàòèçìîâ.
Ïîïðîáóéòå ñóíóòü ðóêó â êèïÿòîê. À òåïåðü, ïîêà åùå æèâà ïàìÿòü î áîëè, ñóíóòü åå òóäà âòîðîé ðàç. Åñëè ó âàñ è âçàïðàâäó õâàòèò äóðîñòè ïðîâåñòè ýòîò îïûò, âû îáíàðóæèòå îáåñêóðàæèâàþùèé ýôôåêò: âû ðóêó ñóåòå, à îíà ÑÀÌÀ ËÅÇÅÒ ÎÁÐÀÒÍÎ! ß íå íàñòàèâàþ, íî, íåñìîòðÿ íà òî, ÷òî âàì ïîòîì ïðèäåòñÿ ìàçàòüñÿ âñÿêèìè ëåêàðñòâàìè îò îæîãà, ýòîò ýêñïåðèìåíò ñòîèò òîãî, ÷òîáû ïðîâåñòè åãî õîòÿ áû ðàç â æèçíè, ïîòîìó ÷òî îùóùåíèå ïî ñâîåé íåîæèäàííîñòè è ôàíòàñòè÷íîñòè óíèêàëüíîå, äàþùåå î÷åíü ÿðêîå, äîñòóïíîå è ýêñêëþçèâíîå ïîíèìàíèå òîãî, ÷òî ó âàñ â ãîëîâå åñòü ñëàáî óïðàâëÿåìûå âàøåé âîëåé ñòðóêòóðû, êîòîðûå ìîãóò ïðåïÿòñòâîâàòü âàøèì íàìåðåíèÿì, îñîáåííî åñëè ýòè íàìåðåíèÿ íåäîñòàòî÷íî ìîòèâèðîâàíû.
È ëàäíî, åñëè ýòî ïðåïÿòñòâîâàíèå òàêîå ïðÿìîëèíåéíîå, êàê â ñëó÷àå ñ êèïÿòêîì íå õî÷ó è íå äàì. Íî âåäü ó ñëîæíîé ëè÷íîñòè è ñïîñîáû áîðüáû íåïðîñòûå: òóò òåáå è âûòåñíåíèå, è ðàöèîíàëèçàöèÿ, è îáåñöåíèâàíèå, è ìíîãî ÷åãî åùå (ñìîòðè ñïèñîê ïñèõîëîãè÷åñêèõ çàùèò), ïðè÷åì âûÿâëåíèå è íåéòðàëèçàöèÿ ýòèõ çàùèò îòäåëüíàÿ ðàáîòà.
À ïàðàäîêñàëüíàÿ ñëîæíîñòü åùå è â òîì, ÷òî íà ýòîò ïðîòåñò ïðîòèâ äèñêîìôîðòà íàêëàäûâàåòñÿ åùå è ïðîòåñò ïðîòèâ ñàìîãî äîñòóïà ê êîðíþ ïðîáëåìû, êîòîðûé (ÿ î ïðîòåñòå) ñôîðìèðîâàëñÿ äàâíî è ìîæåò èìåòü âåñüìà íåòðèâèàëüíóþ, õèòðîóìíóþ è íàäåæíóþ êîíñòðóêöèþ.
…äîïóñòèì, ÷åëîâåê èäåò ïî íî÷íîé óëèöå è âèäèò íà âèòðèíå çàêðûòîãî ìàãàçèíà àïåëüñèí. Îí õî÷åò àïåëüñèí, îí íå ìîæåò åãî ïîëó÷èòü, îí èñïûòûâàåò ôðóñòðàöèþ. Åñëè ïåðåæèâàíèå äîñòàòî÷íî ñèëüíî (êàê ïðàâèëî ýòî íå òàê, çà èñêëþ÷åíèåì âûðàæåííûõ èñòåðîèäîâ), ñðàáàòûâàåò ïñèõîëîãè÷åñêàÿ çàùèòà, íàïðèìåð ïî ìåõàíèçìó «à íàì è íå õîòåëîñü» (íå ïîìíþ, êàê îí ó Êîóëìåíà íàçûâàåòñÿ). ×åëîâåê èäåò è óáåæäàåò ñåáÿ, ÷òî àïåëüñèí îí íå õîòåë, è âàùå… Íî, åñëè ïåðåæèâàíèå äîñòàòî÷íî ñèëüíîå, òî äàëüíåéøèå âñòðå÷è ñ àïåëüñèíîì áóäóò âûçûâàòü ó íåãî âîñïîìèíàíèÿ î íåïðèÿòíîé íî÷è, è ïñèõîëîãè÷åñêàÿ çàùèòà îïÿòü áóäåò âûíóæäåíà âìåøàòüñÿ. Ïîñòåïåííî îíà ñòðîèò çàùèòó âîêðóã ýòîãî âîñïîìèíàíèÿ, ïîòîì çàùèòó âîêðóã ýòîé çàùèòû (ïðèêîñíîâåíèå ê çàùèòå ñàìî ïî ñåáå âîñïðèíèìàåòñÿ êàê òðàâìîîïàñíîå è íåïðèÿòíîå). Òàêèì îáðàçîì, ïîñòåïåííî ÷åëîâåê çàïðåùàåò ñåáå âîñïîìèíàíèÿ î íî÷íîì àïåëüñèíå, çàòåì àïåëüñèíû âîîáùå, çàòåì îðàíæåâûå ñôåðû, çàòåì òåõ, êòî èõ ëþáèò, çàòåì áàñêåòáîë, â êîòîðîì èãðàþò ïîõîæèì íà áîëüøîé àïåëüñèí ìÿ÷îì, çàòåì íåãðîâ, êîòîðûå èãðàþò â áàñêåòáîë…
…
Ïñèõîàíàëèòèê … ëèøü íàïðàâëÿåò êëèåíòà òóäà, ãäå òîìó áîëüíåå. Ïîòîìó ÷òî èìåííî òàì — ãðàäèåíò çàùèòû. ×åì áîëüøå êëèåíò ñîïðîòèâëÿåòñÿ, òåì òî÷íåå îíè èäóò ê öåëè.
«×òî òàêîå ïñèõîàíàëèç»
È âñå ýòè æåñòîêèå ìàíèïóëÿöèè ïñèõîëîãà, íàïîìèíàþ, ïðîèñõîäÿò áåç âîçìîæíîñòè îñîçíàííîãî êîíòðîëÿ è ïîíèìàíèÿ ïðîèñõîäÿùåãî êëèåíòîì.
 òàêîé ñèòóàöèè âïîëíå åñòåñòâåííî è ïîíÿòíî, åñëè â êàêîé-òî ìîìåíò êëèåíò ïîïðîñòó ïåðåñòàíåò ê âàì ïðèõîäèòü, äà åùå è áóäåò ðàññêàçûâàòü âñåì, êàêàÿ âû íåïðîôåññèîíàëüíàÿ è íå÷óòêàÿ ñâîëî÷ü.
Ïîýòîìó íåêîòîðûå ïñèõîëîãè òàê óñåðäíî äåëàþò èäîëà èç äîâåðèÿ êëèåíòà. Äà, äåéñòâèòåëüíî, äîâåðèå øòóêà, êîòîðàÿ ïîçâîëèò âàì ïðîèãíîðèðîâàòü ïðîòåñò è ïîäâèãíåò êëèåíòà íà âçàèìîäåéñòâèå ñ âàìè, íåñìîòðÿ íà êðóãëûå îò îáèæåííîãî óäèâëåíèÿ è íåïîíèìàíèÿ âàøèõ äåéñòâèé ãëàçà. Íî, ê ñîæàëåíèþ, ýòî íå ïàíàöåÿ è ÷ðåâàòî ñâîèìè ïðîáëåìàìè. Êîãäà ïîçèòèâ äîâåðèÿ è ýìîöèîíàëüíîãî êîíòàêòà êîìïëåêòóåòñÿ ýìîöèîíàëüíî íåìîòèâèðîâàííûì ïðè÷èíåíèåì ñòðàäàíèé, òî êëèåíò, åñëè îí íå ìàçîõèñò, îêàçûâàåòñÿ â ñèòóàöèè, âåäóùåé ê íåâðîçó: ïîçèòèâíîå íàìåðåíèå, ïîçèòèâíàÿ æå äåêëàðàöèÿ, è ê òîìó ïðÿìîëèíåéíî íåãàòèâíîå ïîäêðåïëåíèå. Ëàäíî, åñëè âû óñïåëè âñå «âñêðûòü è çàøèòü» äî òîãî, êàê íåâðîç íà÷àë ôîðìèðîâàòüñÿ, à åñëè íåò? Íà äâîéíîé ïðîòåñò ïëþñ íåïîíèìàíèå öåëåñîîáðàçíîñòè ïðîèñõîäÿùåãî íàêëàäûâàåòñÿ íåâðîòè÷åñêàÿ ñèìïòîìàòèêà, óñëîæíÿþùàÿ è çàïóòûâàþùàÿ êàðòèíó, ïëþñ ïîñëåäîâàòåëüíîå ðàçðóøåíèå îñíîâàííîãî íà êðåäèòå äîâåðèÿ, âàøèìè æå ïîñëåäîâàòåëüíûìè óñèëèÿìè.
Ñëîæíî, äà?
Íåò , ÿ, êîíå÷íî, óòðèðóþ, òàêàÿ íåïðîñòàÿ ñèòóàöèÿ âîçíèêàåò íå êàæäûé ðàç, íî, åñëè âû ïðàêòèêóþùèé ïñèõîëîã, òî âû ñåé÷àñ âñïîìèíàåòå ñëó÷àè èç ñâîåé ïðàêòèêè, îòìåííî óêëàäûâàþùèåñÿ â ýòó ñõåìó.
Íî óæ åñëè ñëó÷àé óêëàäûâàåòñÿ, òî, ñàìè ïîíèìàåòå, ïðèäåòñÿ ÷òî-òî ñ ýòèì äåëàòü.
Íà÷íåì ïî ïîðÿäêó.
Âî-ïåðâûõ: äëÿ òîãî, ÷òîáû òåðàïèÿ áûëà óñïåøíîé, çàïðîñ êëèåíòà íå äîëæåí áûòü ôîðìàëüíûì. Îí (êëèåíò) äîëæåí áûòü ýìîöèîíàëüíî çàèíòåðåñîâàí â ðåçóëüòàòå. È åñëè âû çàïëàíèðîâàëè îáúåêòèâíî êà÷åñòâåííûé, êîíñòðóêòèâíûé ðåçóëüòàò, òî ýòîãî îäíîãî íåäîñòàòî÷íî. Íåîáõîäèìî, ÷òîáû êëèåíò îòíåññÿ ê ýòîìó ïëàíèðóåìîìó ðåçóëüòàòó ñ èíòåðåñîì è ýíòóçèàçìîì, ñòðåìëåíèåì. Ýòîò ðåçóëüòàò äîëæåí áûòü âàæåí è æåëàåì. Ýòî íå òîëüêî ñâèäåòåëüñòâî àäåêâàòíîñòè öåëè, íî è óñëîâèå ïðåîäîëåíèÿ ñîïðîòèâëåíèÿ. Åñëè æå ê âàì ïðèøëà ñêó÷àþùàÿ òåòÿ ïîãîâîðèòü ïî äóøàì ñ äîáðîæåëàòåëüíûì ñîáåñåäíèêîì, òî ïðè ìàëåéøåì äèñêîìôîðòå îíà îòïðàâèòñÿ èñêàòü ñîáåñåäíèêà ïîïðèÿòíåå.
Âî-âòîðûõ: â ñîâðåìåííîé ìåäèöèíå (óæå êàêîå-òî âðåìÿ êàê) èìååòñÿ òåíäåíöèÿ, à â íåêîòîðûõ ñòðàíàõ äàæå è ïðàâèëî, îáúÿñíÿòü ïàöèåíòó, ÷òî è çà÷åì âðà÷ äåëàåò è ñîáèðàåòñÿ äåëàòü. Ýòî íå ïóñòîå ýòè÷åñêîå òðåáîâàíèå, ïðîèñõîäÿùåå èç îáùèõ ïðèíöèïîâ ãóìàíèçìà, à ìåòîäè÷åñêèé ïðèåì, íàïðàâëåííûé íà îðãàíèçàöèþ ñèíåðãè÷åñêîãî ñîòðóäíè÷åñòâà âðà÷à è ïàöèåíòà. ß ñ÷èòàþ, ÷òî è â ïñèõîëîãèè ýòîò ïðèíöèï ðàáîòàåò. Âìåñòî «äåëàéòå, ÷òî ãîâîðþ, ÿ ëó÷øå çíàþ», â áîëüøèíñòâå ñëó÷àåâ èìååò ñìûñë âåñòè ëèíèþ: «Ó íàñ òàêàÿ-òî ñèòóàöèÿ, êîòîðóþ, êàê ìíå èçâåñòíî, ëó÷øå âñåãî îáðàáàòûâàòü òàêèì-òî îáðàçîì, äëÿ ÷åãî ÿ äîëæåí äåëàòü òàê, à âû âîò òàê, è òîãäà âîò òàêèì îáðàçîì ó íàñ ïîëó÷èòñÿ òî-òî è òî-òî». È ñëåäóåò äîáèâàòüñÿ äåéñòâèòåëüíî ÷åòêîãî ïîíèìàíèÿ êëèåíòîì ïðîèñõîäÿùåãî, äàæå åñëè êàêîå-òî âðåìÿ ïðèäåòñÿ ïîòðàòèòü íà ïðîñâåòèòåëüñêóþ ðàáîòó. Ïî êðàéíåé ìåðå, ÿ ïîñòóïàþ èìåííî òàê, è, åñëè âû êî ìíå îáðàòèòåñü, âû áóäåòå çíàòü, ÷òî ÿ â îòíîøåíèè âàñ ïðåäïîëîæèë, ïî êàêèì ïðè÷èíàì, êàê ìû ýòî ïðåäïîëîæåíèå ïðîâåðèì, ÷òî áóäåì äåëàòü, åñëè îíî îïðàâäàåòñÿ, è ïî÷åìó èìåííî ýòî.
Óâû, åñòü è ñëîæíîñòü. Íåêîòîðûå ïðîöåññû äîñòóïíû òîëüêî â ñëó÷àå, åñëè êëèåíò î íèõ íå ïîäîçðåâàåò, òàê êàê îíè íàïðàâëåíû íà îáõîä çàùèòû, îáìàí ïðîòåñòíûõ ñòðóêòóð. Ýòî ïðîòèâîðå÷èå (íå êàæóùååñÿ, à âïîëíå ðåàëüíîå) ïðèõîäèòñÿ îáõîäèòü òåì æå îáðàçîì: ðàçúÿñíÿòü ñóòü çàùèò è ìåõàíèçìîâ ôîðìèðîâàíèÿ ïðîòåñòà, äîáèâàòüñÿ ïîíèìàíèÿ, è ïîëó÷åíèÿ èíôîðìèðîâàííîãî ñîãëàñèÿ íà ìàíèïóëÿòèâíîå ñîêðûòèå îò êëèåíòà êàêèõ-òî âàøèõ èäåé. Ýòî ðàáîòàåò, íî óâû, òðåáóåò îò êëèåíòà îïðåäåëåííîãî èíòåëëåêòà, ÷òî ñëó÷àåòñÿ íå âñåãäà. Òàê ÷òî, êàê íè êðóòè, à âðåìåíàìè ïðèõîäèòñÿ âìåñòî ðåàëüíîé êàðòèíû ïîäàâàòü àëüòåðíàòèâíóþ, ïîïðîùå, äîñòóïíóþ äëÿ âîñïðèÿòèÿ íåèñêóøåííûì óìîì. Çíàåòå, êàê îïûòíûå ìåäñåñòðû äåëàþò èíúåêöèè äåòÿì? Ùåëêàþò ïàëüöåì íàä óõîì, à ñàìè èãîëêó â ïîïó ððàç! Ðåáåíîê è íå çàìåòèë, êàê ïîëó÷èë óêîë.
Â-òðåòüèõ, íå ñëåäóåò çëîóïîòðåáëÿòü äîâåðèåì êàê èíñòðóìåíòîì. Îíî, êàê ÿ ïîêàçàë âûøå, óñëîâíî óäîáíî è îãðàíè÷åíî ïî çàïàñó. Åñëè êëèåíò ïðîäîëæàåò ê âàì õîäèòü òîëüêî ïîâåðèâ âàì íà ñëîâî, ÷òî âñå èäåò êàê íàäî, òî åñëè ðåçåðâ äîâåðèÿ èññÿêíåò íå âîâðåìÿ, âû ðèñóåòå ïðîâàëèòü òåðàïèþ. Òàê ÷òî, ïðåæäå âñåãî, äîâåðèå, åñëè óæ âû ñîáèðàåòåñü åãî èñïîëüçîâàòü, ñëåäóåò ïîäêðåïëÿòü èíôîðìèðîâàíèåì êëèåíòà â ïðîöåññå òåðàïèè. Êðîìå òîãî, íàäî ó÷èòûâàòü, ÷òî ýòî èìåííî èíñòðóìåíò, è, êîëü óæ ñêîðî ïðèøëà ïîðà èì âîñïîëüçîâàòüñÿ, òî íîðìàëüíî ôîðñèðîâàòü åãî ìàíèïóëÿòèâíûìè ñðåäñòâàìè, è íåîáõîäèìî êîíòðîëèðîâàòü ðàçìåðû åãî çàïàñà. Ïîýòîìó, êñòàòè, ìíå î÷åíü íå íðàâèòñÿ, êîãäà ïñèõîëîã èñïîëüçóåò äîâåðèå êëèåíòà êàê îñíîâó òåðàïèè è êàê ñðåäñòâî ïîëó÷åíèÿ ñîáñòâåííûõ ýìîöèîíàëüíûõ ïëþøåê. Ýòî íåïðîôåññèîíàëüíî.
Â-÷åòâåðòûõ, ñëåäóåò äîáèâàòüñÿ îñîçíàííîãî îòíîøåíèÿ êëèåíòà ê ïðîáëåìå. Ýòî íå îçíà÷àåò, ÷òî îí äîëæåí ïîíèìàòü åå òàê æå õîðîøî, êàê âû, è îòíîñèòüñÿ ê íåé òàê æå ìåòîäè÷íî, êàê âû. Áóäåò ïðàâèëüíî è äîñòàòî÷íî, åñëè ó íåãî â ñîçíàíèè ñîçäàñòñÿ âåêòîð âíèìàíèÿ, íàïðàâëåííûé èìåííî íà ñóòü ïðîáëåìû, è òîãäà ôîðìèðóåìûé ïðîòåñò ìîæíî áóäåò íàïðàâèòü èìåííî íà íåå, à íå íà âàñ è íå íà âàøè ìåòîäû. Áîëüíî íå ïîòîìó, ÷òî âû ãàä, è íå ïîòîìó, ÷òî âàøè ìåòîäû äóðàöêèå, à ïîòîìó, ÷òî ïðîáëåìà òàêàÿ. Ïëîõàÿ ïðîáëåìà, ôóáÿêà, àòó åå âñå âìåñòå.
Ñëîæíîñòü åñòü è çäåñü: äëÿ òîãî, ÷òîáû ðàáîòàòü ñ êàêîé-òî ñòðóêòóðîé ëè÷íîñòè, íàäî åå ñíà÷àëà ïðèíÿòü. Îíî è åñòåñòâåííî: ÷òîáû ìàíèïóëèðîâàòü ëþáûì îáúåêòîì, åãî äëÿ ýòîãî íàäî óâèäåòü è âçÿòü â ðóêè (óñëîâíî ãîâîðÿ). «À òåïåðü äàâàéòå âîçüìåì æàáó». Ïîä ïðèíÿòèåì ÿ ðàçóìåþ íå òîëåðàíòíîå îòíîøåíèå, à ïðèçíàíèå è íàáëþäåíèå. Ýòî òðåáóåò îïðåäåëåííîãî öèíèçìà (â äàííîì êîíòåêñòå ãîòîâíîñòè âîñïðèíèìàòü ðåàëüíîñòü âî âñåõ åå ïðîÿâëåíèÿõ), êîòîðûé ñâîéñòâåíåí íå âñåì. Èíîãäà ïðèõîäèòñÿ åãî ôîðìèðîâàòü ïðÿìî â ïðîöåññå òåðàïèè. Åñëè ýòî íå óäàåòñÿ, ìîæíî èñïîëüçîâàòü ìåòàôîðû. Íî ìåòàôîðû òîæå èìåþò ñâîè ãðàíèöû, òàê ÷òî, åñëè âû íå ìàñòåð òî÷íûõ ìåòàôîð, òî ìîãóò áûòü òðåòè÷íûå ñëîæíîñòè. À òî è ÷åòâåðòè÷íûå.  îáùåì, ýòî, íàâåðíîå, òåìà äëÿ îòäåëüíîé ñòàòüè.
Â-ïÿòûõ, íàäî çàðàíåå ðàçúÿñíèòü êëèåíòó, ÷òî íà êàêîì-òî ýòàïå âåðîÿòíû ñóáúåêòèâíûå óõóäøåíèÿ ñàìî÷óâñòâèÿ, îáúÿñíèòü, ïî÷åìó òàê ïðîèñõîäèò (îïÿòü-òàêè ìîæíî ïðè ïîìîùè ìåòàôîð), è çàðàíåå ñïëàíèðîâàòü, êàê êëèåíò áóäåò ýòî óõóäøåíèå ïðîæèâàòü è îáðàáàòûâàòü.
Â-øåñòûõ, â ñëó÷àå íåîáõîäèìîñòè èìååò ñìûñë, îïÿòü-òàêè â ïîðÿäêå ìàíèïóëÿöèè, êîìïåíñèðîâàòü íåãàòèâíûå âïå÷àòëåíèÿ êàêèìè-íèáóäü ðàäîñòíûìè äëÿ êëèåíòà èãðóøêàìè, ïóñòü è áåñïîëåçíûìè. Ïñèõîëîãè÷åñêèìè ôîêóñàìè, òåñòàìè (îñîáåííî ïðîåêòèâíûìè), èãðàìè, ÷òî ìîæåò óðàâíîâåñèòü íåâðîçîîáðàçóþùåå íåãàòèâíîå ïîäêðåïëåíèå. Åñòü äàæå öåëûé êëàí «ïñèõîëîãîâ», êîòîðûå áîëüøå íè÷åãî íå äåëàþò, òåì è æèâóò.
Â-ñåäüìûõ, íåçàâèñèìî îò ðåàëüíîé íàäîáíîñòè, íàäî â êîíöå òåðàïèè ïîòðàòèòü êàêîå-òî âðåìÿ íà îñîçíàíèå íîâûõ âîçìîæíîñòåé è õîòÿ áû îáùóþ ïðîðàáîòêó ñâÿçàííûõ ñ íèìè ïëàíîâ, ñ óïîðîì íà îïòèìèçì. Ýòî äàñò ñòðàòåãè÷åñêîå ïîçèòèâíîå ïîäêðåïëåíèå, îðèåíòèðóþùåå íà ãîòîâíîñòü ê ðàáîòå ñ ïñèõîëîãîì â ñëó÷àå íåîáõîäèìîñòè â áóäóùåì.
Íó è ïðîñòî, ÷òîáû îïðàâäàòü íàçâàíèå ñòàòüè:
Çàêîí Îìà ãëàñèò, ÷òî ñèëà òîêà (åñëè äîñëîâíî ïåðåâîäèòü ñ àíãëèéñêîãî, «ïîòîêà») ïðÿìî ïðîïîðöèîíàëüíà íàïðÿæåíèþ è îáðàòíî ïðîïîðöèîíàëüíà ñîïðîòèâëåíèþ. Òî æå ñàìîå ñîîòíîøåíèå ðàáîòàåò è â ïñèõîëîãèè. Äëÿ òîãî, ÷òîáû ïîòîê ïîøåë, íåîáõîäèìî «íàïðÿæåíèå»: èíèöèàòèâà, âîëÿ, çàèíòåðåñîâàííîñòü. È ÷åì îíî áóäåò âûøå, òåì ñèëüíåå áóäåò ïîòîê. È òåì ñèëüíåå îí áóäåò, ÷åì ìåíüøå áóäåò ñîïðîòèâëåíèå. Îòñþäà ïîòðÿñàþùàÿ ïî ñâîåé òî÷íîñòè àíàëîãèÿ: ìû ðàáîòàåì íà ïîâûøåíèå ýìîöèîíàëüíîé àêòóàëüíîñòè çàïðîñà è íà ñíèæåíèå ñîïðîòèâëåíèÿ. Ïðè ýòîì íàëè÷èå âûñîêîãî íàïðÿæåíèÿ ïðè áîëüøîì ñîïðîòèâëåíèè ìîæåò äàòü íå ïîòîê, à ïðîáîé, àâàðèþ, ïîýòîìó ñíèæåíèå èìåþùåãîñÿ ñîïðîòèâëåíèÿ çàäà÷à, âàæíîñòü êîòîðîé íå ïåðåîöåíèòü.
Äëÿ ñïðàâêè ãóìàíèòàðèÿì: ìîùíîñòü â ýëåêòðîòåõíèêå îïðåäåëÿåòñÿ êàê ïðîèçâåäåíèå íàïðÿæåíèÿ íà ñèëó òîêà.
Источник

