Чем полезна математика в изучении языков

Сможете ли вы доступно объяснить ребёнку, для чего ему нужно заниматься математикой? Ведь изучение понятий, законов математики и логики, решение математических и логических задач требует умственных усилий. А зачем вообще это нужно?
Мы изучили ряд научных исследований, и выделили реальные доказательства пользы от занятий математикой.
Даже если вы убеждены, что жизнь вашего ребенка не будет связана с математикой, рекомендуем все равно прочитать нашу статью, чтобы как минимум с легкостью ответить на вопросы маленького «почемучки».
1. Математика развивает мышление
Изучая математику и решая задачи, ребёнок учится:
- обобщать и выделять важное;
- анализировать и систематизировать;
- находить закономерности и устанавливать причинно-следственные связи;
- рассуждать и делать выводы;
- мыслить логически, стратегически и абстрактно.
Как регулярные спортивные тренировки «прокачивают» тело, делают его здоровым, сильным и выносливым, так регулярные занятия математикой «прокачивают» мозг – развивают интеллект и познавательные способности, расширяют кругозор.
Читайте также:
В статье «5 причин научиться думать как математик» мы подробно разобрали в чем заключается сила математического мышления и зачем его развивать.
2. Занятия математикой тренируют память
Ученые из Стэнфордского университета в США изучили процесс решения человеком математических задач и выяснили, что взрослые люди используют для этих целей мышление и доведенный до автоматизма навык «доставать» из памяти уже имеющиеся там ответы.
Дети до 7 лет часто прибегают к помощи пальцев рук и ног, а также различных заменителей (реальных предметов, счетных палочек). В «переходный период», в возрасте от 7 до 9 лет, у школьников формируется «взрослый» навык «думания», осмысления и запоминания информации.
Интересное исследование было опубликованно в журнале «Nature Neuroscience» в 2014 году. В первую очередь, оно было посвящено изучению роли гиппокампа (области в головном мозге) в развитии познавательной активности детей. Но его косвенные выводы таковы:
- если хотите, чтобы у ребенка в школе не было проблем с математикой – тренируйте память в раннем возрасте;
- решение математических задач развивает память.
3. Математика закаляет характер
Для правильного решения математических и логических задач нужны внимательность, настойчивость, ответственность, точность и аккуратность.

Чем регулярнее ребенок тренирует эти «мышцы характера», тем сильнее они становятся, тем чаще помогают ребенку в решении не только учебных задач, но и жизненных проблем.
ЛогикЛайк – подходящая платформа для тренировок по 20-60 минут в день. Решайте задачи, участвуйте в олимпиадах по логике и математике, развивайте волю к победе и умение побеждать!
Мы создаём и простые, и олимпиадные задачи, которые хочется решать:
4. Музыка для математики, математика – для музыки
Комплексное исследование, проведенное Барбарой Хелмрич (Barbara H. Helmrich) из Колледжа Нотр-Дам в Балтиморе, выявило, что дети, которые играли на музыкальных инструментах в средней школе, ощутимо лучше успевают по математике в старших классах.
Ученые обнаружили, что за решение алгебраических задач и обработку музыкальной информации отвечает один и тот же участок головного мозга.
«Наибольшая средняя разница в результатах по алгебре между любыми двумя группами испытуемых была обнаружена между афроамериканскими «инструментальными» группами и группами «немузыкальных» школьников».
Парадоксально, но ученые как будто не интересовались обратной связью.
Ведь если за развитие математических и музыкальных способностей отвечает один и тот же участок головного мозга, не исключено, что занятия математикой улучшают музыкальные способности.
Вспоминается Шерлок Холмс, который был одновременно превосходным сыщиком и талантливым скрипачом. Многие скажут, что знаменитый английский сыщик – просто выдумка, но у него был свой реальный прототип, наставник и друг Артура Конана Дойла. Страстным скрипачом был и величайший физик Альберт Эйнштейн.
5. Математика помогает преуспевать в гуманитарных науках
Именно ранние математические способности – верная предпосылка к тому, что в дальнейшем ребенок будет не только хорошо понимать математику, но и преуспевать в других школьных дисциплинах. Далее по значимости вклада в учебные успехи идут навыки чтения и способности управлять своим вниманием.
К таким выводам пришли ученые в области образования и социальной политики Северо-Западного университета в Эванстоне. В ходе исследования они оценивали связь ключевых элементов готовности к школе (базовые навыки для приема в школу — «академическая» готовность, внимание, социально-эмоциональные навыки) с дальнейшими успехами в учебе.
Математика – наука междисциплинарная, она тесно связана с физикой, географией, геологией, химией. Социология и экономика неотделимы от математики, и многие выводы даже привычно гуманитарных наук, таких как лингвистика, журналистика, опираются на математические модели и понятия, математические и логические законы.
6. Развивает навыки решения бытовых задач
Барбара Оакли, доктор технических наук, исследователь стволовых клеток мозга и автор книги «Думай как математик» подчеркивает:
«Математика избавляет нас от «магического мышления» – мы стремимся вникнуть в суть вещей и не полагаемся на авось и высшие силы».
Чем сложнее становятся математические задачи, тем больше навыков требуется для их решения. Ребенок учится рассуждать, выстраивать последовательности, продумывать алгоритмы, жонглировать сразу несколькими понятиями, и эти навыки входят в привычку.
Благодаря математике мы избавляемся от вредных привычек:
- не домысливаем, а оперируем только точными терминами;
- не просто механически запоминаем информацию и правила, а оцениваем ее, анализируем, размышляем, чтобы понять и усвоить новый материал, новый жизненный урок.
7. Математика – основа успешной карьеры
Если 10-15 лет назад перспективным считалось изучение иностранных языков, то сейчас свободным владением несколькими языками никого не удивишь. Теперь профессиональная востребованность во многом зависит от понимания технологий, умения мыслить, абстрагироваться и способностей к решению нестандартных задач. Крайне сложно обойтись без знания математики тем, кто хочет работать в сфере IT.
Абстрактное, критическое и стратегическое мышление, аналитические способности, умение выстраивать алгоритмы – «мастхэв» для хорошего разработчика.

ТОП 5 гибких навыков. Источник: amazonaws.com
Результативные занятия математикой придают уверенность в себе, ведь успехи в ней требуют упорства в стремлении решить самые сложные, иногда, на первый взгляд, «неразрешимые» задачи и проблемы.
Проверьте свои силы:
Математические головоломки вам в помощь: 9 отборных известных задач на сообразительность. Сколько сможете решить?
8. Решение задач вырабатывает психологическую стойкость
Решение математических задач помогает улучшить эмоциональный фон – это занятие способно избавить от тревоги, помогает контролировать эмоции и предупреждает стресс.
К таким выводам пришли ученые из Университета Дьюка в США, которые сумели доказать это в исследовании, опубликованном в журнале «Клиническая психология» в 2016 году.
9. Удовольствие от «икс»
Для человека, серьёзно занимающегося математикой, математические формулы, уравнения и другие логические и математические задачи воплощают собой красоту, гармонию и доставляют такое же эстетическое удовольствие, как музыка, искусство и хорошая шутка, утверждает группа исследователей из нескольких университетов Великобритании.
С помощью функциональной магнитно-резонансной томографии была зафиксирована активность мозговой деятельности испытуемых во время демонстрации им математических уравнений, формул и задач. Результаты исследования опубликованы в журнале «Границы человеческой нейробиологии» (Frontiers in Human Neuroscience) в 2014 году.
Как научиться испытывать радость и наслаждение от занятий математикой рассказывает известный американский математик, выпускник Гарвардского университета, Стивен Строгац. Преподаватель прикладной математики, обладатель наград в области математики и преподавания на страницах своей книги «Удовольствие от X» с энтузиазмом, просто и понятно объясняет самые значительные математические идеи.
Попробуйте занятия логикой и математикой на LogicLike.com!
Мы убеждены, что детям, особенно в возрасте 5-9 лет, не обязательно рассказывать, как важно изучать математику. Гораздо важнее дать возможность ребёнку окунуться в мир занимательной интерактивной математики.

Обучаясь на платформе LogicLike, дети решают интересные логические задачи, зарабатывают за правильные ответы свои первые награды-«звезды», играют в современные логические игры – и получают не только пользу, но и настоящее удовольствие от такой математики.
Источник

Джордж Зипф
Лингвистика — это наука, которая требует усидчивости и даже математических наклонностей. Наш блогер Марк Блау часто рассказывает об интересных учёных в этой области знаний. Сегодня он делится тем, как связаны графики со словами, и рассказывает, какой словарь поможет научиться читать на иностранном языке за год.
Рассылка «Мела»
Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу
Кто такой Джордж Зипф
«В каждой естественной науке заключено столько истины, сколько в ней есть математики» (Иммануил Кант). Математикам свойственен некоторый снобизм. Вслед за И. Кантом они считают, что в каждом разделе знания есть лишь столько настоящей науки, сколько в нём математики. Они недалеки от истины. Математика — это концентрированная логика, а любая наука претендует на то, чтобы быть логичной, точной и однозначной в своих утверждениях. Поэтому, насколько это возможно, любая наука старается использовать математические методы.
Американский ученый Джордж Кингсли Зипф (George Kingsley Zipf; 1902–1950) знаменит тем, что первым применил в лингвистике статистические методы, то есть «обвенчал» филологию с математикой. Зипф — американец, но его фамилия явно немецкого происхождения. В силу этого по-русски её могут читать и произносить трояко: и Ципф, и Зипф, и Зиф. Об этом следует помнить, ведя поиск информации об учёном в русскоязычном интернете.
В 1923 году Джордж Зипф поступил в Гарвардский колледж, который окончил с отличием через год. Своё образование филолога Зипф продолжил в Германии. Он учился сначала в Берлинском, а потом в Боннском университете. Именно здесь он пришёл к убеждению, что язык необходимо исследовать как природное явление, потому что он является не результатом соглашения между людьми, а результатом некоторого естественного процесса коммуникации. Оказалось, что этот процесс можно исследовать математическими методами.
Начать эти исследования Зипфу удалось позже. Пока же, возвратившись из Германии в США, он защитил в Гарвардском университете докторскую диссертацию по сравнительной филологии и остался работать преподавателем немецкого языка. Одновременно с преподавательской работой он вёл научную деятельность, продолжал свои работы в области лингвистики и уже в 1935 году издал книгу «Психобиология языка», которая была впоследствии издана в Европе — в Германии и во Франции.
В годы Второй мировой войны Зипф вёл в Гарвардском университете курс немецкого языка для начинающих. Как преподаватель он поставил своей целью организовать учебный процесс таким образом, чтобы значительно ускорить изучение языка. В частности, Зипф добивался того, чтобы к концу первого года обучения студент мог бы читать по-немецки со словарём.
В ходе своей преподавательской работы, применяя методы математической статистики к языку, он открыл закон, который впоследствии был назван в его честь
Этот закон оказал большое влияние на развитие лингвистики, в частности на внедрение в неё математических методов исследования.
К сожалению, жизнь учёного оказалась недолгой. В 1950 году врачи обнаружили у него злокачественную опухоль. Сделанная операция не помогла, и 25 сентября 1950 года Джордж Зипф скончался.
Закон Зипфа
Закон «имени себя» Джордж Зипф открыл, будучи преподавателем иностранного языка. Он задумался над совершенствованием методики преподавания, чтобы повысить эффективность обучения.
Одна из сторон процесса изучения чужого языка — расширение словарного запаса. Хочешь говорить на языке — учи слова этого языка. Конечно, учить их, читая словарь, что называется, от корки до корки и запоминая все встречающиеся в алфавитном порядке слова, — способ не самый лучший. Одни слова встречаются в языке чаще, а другие реже. Некоторые — совсем редко.
Вы знаете, что такое тантамареска и чем она отличается от тинтамара? Между тем эти слова входят в словарь русского языка. Правда, они очень редкие
Словарный запас нужно расширять по другому принципу. В первую очередь следует учить наиболее употребительные слова. Таких слов относительно немного — около 2000. Сначала следует осваивать наиболее часто употребляемые в языке слова, потом — слова, которые используются реже, и, наконец, слова, применяемые совсем редко, для украшения и индивидуализации речи.
Если уж и учить иностранные слова по словарю, то словарь этот должен быть не алфавитным, а частотным. В частотном словаре слова располагаются не по алфавиту, а по частоте встречаемости в текстах на изучаемом языке. Например, слово, которое в алфавитном словаре, состоящем из миллиона слов, встретится 100 тысяч раз, в частотном словаре будет стоять раньше слова, частота встречаемости которого 10 тысяч раз на миллион. В свою очередь, это второе слово будет находиться в частотном словаре ближе к началу, чем слово, встречающееся только тысячу раз на миллион слов.
Позицию слова в частотном словаре иначе называют рангом этого слова. Чем выше ранг слова, тем реже оно встречается в языке, тем дальше от начала это слово находится в частотном словаре. Очевидно, что у служебных слов (предлогов, артиклей и так далее) будет самый низкий ранг. Эти слова встречаются в тексте часто, но, как правило, они короткие и большой смысловой нагрузки не несут. Уже в первом десятке слов частотного словаря появятся и слова значащие. Именно их следует давать студенту при обучении в первую очередь. Так что частотный словарь изучаемого языка насущно необходим студенту, а ещё более — преподавателю.
Чтобы создать такой словарь, надо посчитать частоту встречаемости всех слов определённого языка и расположить их по мере убывания этого параметра. Здесь возникают две проблемы. Во-первых, выбрать текст или группу текстов, которые могли бы представлять весь язык. Набор текстов, способный представлять весь язык в целом, называют ещё корпусом языка. Лингвисты считают, что объём корпуса языка должен быть не менее миллиона слов, а составлять его следует из самых разных источников, от газетных статей до классических текстов. Дело это очень ответственное и требующее настоящего филологического чутья.
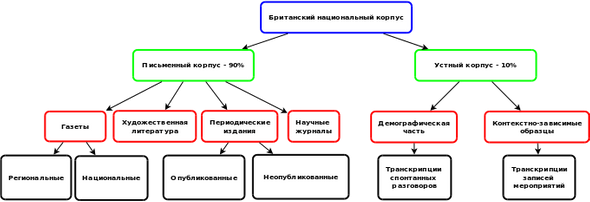
Из каких источников образуется корпус английского языка
Вторая проблема — огромный объём вычислений. После того как составлен корпус языка, надо посчитать частоты встречаемости для каждого из слов. До появления компьютеров это было технически невозможно. Сейчас же простенькую программку для компьютера, считающую частоту встречаемости слов, может написать и сообразительный школьник, но проблем от этого не стало меньше, они просто перешли на другой уровень сложности.
Поэтому частотные словари появились относительно недавно. Первый такой словарь английского языка, «The Teacher’s Word Book», вышел в свет в 1921 году. Этот словарь включал 10 тысяч самых употребительных английских слов. В 1944 году он был переиздан в увеличенном объёме (30 тысяч слов). Первый частотный словарь русского языка тоже был издан в США в 1953 году. Он содержал около 5 тысяч слов. Первый частотный словарь современного русского языка появился в 1963 году в Таллине. В нём было представлено две с половиной тысячи наиболее употребительных слов. В 1977 году был издан первый частотный словарь русского языка, который создали с помощью компьютера на базе корпуса текстов в миллион слов.
В любом случае понятно, почему, будучи преподавателем иностранного языка в Гарвардском университете, Джордж Зипф заинтересовался проблемой частоты встречаемости слов в языке. Его первая работа в этой области вышла в 1932 году. Зипф исследовал частоту распределения слов в таких далеких друг от друга языках, как латынь и китайский. Китайского языка Зипф не знал, но в это время у него работал аспирант-китаец и несколько студентов-китайцев. Они сделали главную часть работы по подбору корпуса текстов на этом языке.
Затем отдельно по латинскому и по китайскому корпусу определялась частота встречаемости каждого из входящих в него слов. После чего были составлены частотные словари. Для этого все слова латинского языка расположили в порядке убывания частоты встречаемости (возрастания рангов). Точно так же был составлен частотный словарь китайского языка.
Оказалось, что произведение частоты встречаемости слова и его ранга в частотном словаре для каждого языка — величина постоянная
Аналитически закон Зипфа можно было выразить формулой fr = c, где f — частота встречаемости слова в тексте; r — ранг (порядковый номер) слова в частотном словаре; с — постоянная величина, значение которой различается для разных языков.
Кривая, описывающая закон Зипфа, — гипербола, довольно быстро спадающая и с тянущимся затем почти горизонтальным «хвостом». В спадающей части этой кривой находятся самые употребляемые слова, а в хвосте — слова, употребляемые редко. Зато именно в этой части происходят многие чудеса, благодаря которым в языке появляются новые слова, но об этом в следующий раз.
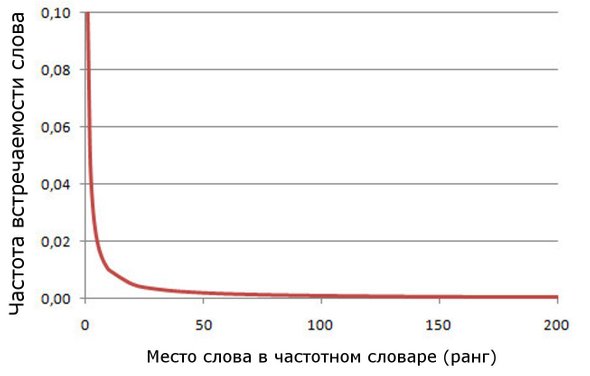
Кривая, выражающая закон Зипфа, — гипербола
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Источник

