Чему равна полезная работа если совершенная работа


1. Механическая работа ( A ) — физическая величина, равная произведению вектора силы, действующей на тело, и вектора его перемещения: ( A=vec{F}vec{S} ). Работа — скалярная величина, характеризуется числовым значением и единицей.
За единицу работы принимают 1 джоуль (1 Дж). Это такая работа, которую совершает сила 1 Н на пути 1 м.
[ [,A,]=[,F,][,S,]; [,A,]=1Нcdot1м=1Дж ]
2. Если сила, действующая на тело, составляет некоторый угол ( alpha ) с перемещением, то проекция силы ( F ) на ось X равна ( F_x ) (рис. 42).
Поскольку ( F_x=Fcdotcosalpha ), то ( A=FScosalpha ).
Таким образом, работа постоянной силы равна произведению модулей векторов силы и перемещения и косинуса угла между этими векторами.
3. Если сила ( F ) = 0 или перемещение ( S ) = 0, то механическая работа равна нулю ( A ) = 0. Работа равна нулю, если вектор силы перпендикулярен вектору перемещения, т.е. ( cos90^circ ) = 0. Так, нулю равна работа силы, сообщающей телу центростремительное ускорение при его равномерном движении по окружности, так как эта сила перпендикулярна направлению движения тела в любой точке траектории.
4. Работа силы можетбыть как положительной, так и отрицательной. Работа положительная ( A ) > 0, если угол 90° > ( alpha ) ≥ 0°; если угол 180° > ( alpha ) ≥ 90°, то работа отрицательная ( A ) < 0.
Если угол ( alpha ) = 0°, то ( cosalpha ) = 1, ( A=FS ). Если угол ( alpha ) = 180°, то ( cosalpha ) = -1, ( A=-FS ).
5. При свободном падении с высоты ( h ) тело массой ( m ) перемещается из положения 1 в положение 2 (рис. 43). При этом сила тяжести совершает работу, равную:
[ A=F_тh=mg(h_1-h_2)=mgh ]
При движении тела вертикально вниз сила и перемещение направлены в одну сторону, и сила тяжести совершает положительную работу.
Если тело поднимается вверх, то сила тяжести направлена вниз, а перемещение вверх, то сила тяжести совершает отрицательную работу, т.е.
[ A=-F_тh=-mg(h_1-h_2)=-mgh ]
6. Работу можно представить графически. На рисунке изображён график зависимости силы тяжести от высоты тела относительно поверхности Земли (рис. 44). Графически работа силы тяжести равна площади фигуры (прямоугольника), ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс
в точке ( h ).
Графиком зависимости силы упругости от удлинения пружины является прямая, проходящая через начало координат (рис. 45). По аналогии с работой силы тяжести работа силы упругости равна площади треугольника, ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс в точке ( x ).
( A=Fx/2=kxcdot x/2 ).
[ F=kx^2/2 ]
7. Работа силы тяжести не зависит от формы траектории, по которой перемещается тело; она зависит от начального и конечного положений тела. Пусть тело сначала перемещается из точки А в точку В по траектории АВ (рис. 46). Работа силы тяжести в этом случае
[ A_{AB}=mgh ]
Пусть теперь тело движется из точки А в точку В сначала вдоль наклонной плоскости АС, затем вдоль основания наклонной плоскости ВС. Работа силы тяжести при перемещении по ВС равна нулю. Работа силы тяжести при перемещении по АС равна произведению проекции силы тяжести на наклонную плоскость ( mgsinalpha ) и длины наклонной плоскости, т.е. ( A_{AC}=mgsinalphacdot l ). Произведение ( lcdotsinalpha=h ). Тогда ( A_{AC}=mgh ). Работа силы тяжести при перемещении тела по двум различным траекториям не зависит от формы траектории, а зависит от начального и конечного положений тела.
Работа силы упругости также не зависит от формы траектории.
Предположим, что тело перемещается из точки А в точку В по траектории АСВ, а затем из точки В в точку А по траектории ВА. При движении по траектории АСВ сила тяжести совершает положительную работу, при движении по траектории В А работа силы тяжести отрицательна, равная по модулю работе при движении по траектории АСВ. Следовательно работа силы тяжести по замкнутой траектории равна нулю. То же относится и к работе силы упругости.
Силы, работа которых не зависит от формы траектории и по замкнутой траектории равна нулю, называют консервативными. К консервативным силам относятся сила тяжести и сила упругости.
8. Силы, работа которых зависит от формы пути, называют неконсервативными. Неконсервативной является сила трения. Если тело перемещается из точки А в точку В (рис. 47) сначала по прямой, а затем по ломаной линии АСВ, то в первом случае работа силы трения ( A_{AB}=-Fl_{AB} ), а во втором ( A_{ABC}=A_{AC}+A_{CB} ), ( A_{ABC}=-Fl_{AC}-Fl_{CB} ).
Следовательно, работа ( A_{AB} ) не равна работе ( A_{ABC} ).
9. Мощностью называется физическая величина, равная отношению работы к промежутку времени, за который она совершена. Мощность характеризует быстроту совершения работы.
Мощность обозначается буквой ( N ).
[ N = A/t ]
Единица мощности: ( [N]=[A]/[t] ). ( [N] ) = 1 Дж/1 с = 1 Дж/с. Эта единица называется ватт (Вт). Один ватт — такая мощность, при которой работа 1 Дж совершается за 1 с.
10. Мощность, развиваемая двигателем, равна: ( N = A/t ), ( A=Fcdot S ), откуда ( N=FS/t ). Отношение перемещения ко времени представляет собой скорость движения: ( S/t = v ). Откуда ( N = Fv ).
Из полученной формулы видно, что при постоянной силе сопротивления скорость движения прямо пропорциональна мощности двигателя.
В различных машинах и механизмах происходит преобразование механической энергии. За счёт энергии при её преобразовании совершается работа. При этом на совершение полезной работы расходуется только часть энергии. Некоторая часть энергии тратится на совершение работы против сил трения. Таким образом, любая машина характеризуется величиной, показывающей, какая часть передаваемой ей энергии используется полезно. Эта величина называется коэффициентом полезного действия (КПД).
Коэффициентом полезного действия называют величину, равную отношению полезной работы ( (A_п) ) ко всей совершённой работе ( (A_с) ): ( eta=A_п/A_с ). Выражают КПД в процентах.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Работа определяется по формуле
1) ( A=Fv )
2) ( A=N/t )
3) ( A=mv )
4) ( A=FS )
2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае
1) равна нулю
2) положительная
3) отрицательная
4) больше работы силы упругости
3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?
1) 300 Дж
2) 150 Дж
3) 3 Дж
4) 1,5 Дж
4. Искусственный спутник Земли, масса которого равна ( m ), равномерно движется по круговой орбите радиусом ( R ). Работа, совершаемая силой тяжести за время, равное периоду обращения, равна
1) ( mgR )
2) ( pi mgR )
3) ( 2pi mgR )
4) ( 0 )
5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?
1) -960 кДж
2) -96 кДж
3) 960 кДж
4) 96 кДж
6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?
1) 0,25 Дж
2) 5 Дж
3) 250 Дж
4) 500 Дж
7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?
1) 1
2) 2
3) 3
4) работа во всех случаях одинакова
8. Работа по замкнутой траектории равна нулю
А. Силы трения
Б. Силы упругости
Верным является ответ
1) и А, и Б
2) только А
3) только Б
4) ни А, ни Б
9. Единицей мощности в СИ является
1) Дж
2) Вт
3) Дж·с
4) Н·м
10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?
1) 40000 Дж
2) 1000 Дж
3) 400 Дж
4) 25 Дж
11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.
РАБОТА СИЛЫ
A. Работа силы упругости при растяжении пружины
Б. Работа силы трения
B. Работа силы тяжести при падении тела
ЗНАК РАБОТЫ
1) положительная
2) отрицательная
3) равна нулю
12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.
1) Работа силы тяжести не зависит от формы траектории.
2) Работа совершается при любом перемещении тела.
3) Работа силы трения скольжения всегда отрицательна.
4) Работа силы упругости по замкнутому контуру не равна нулю.
5) Работа силы трения не зависит от формы траектории.
Часть 2
13. Лебёдка равномерно поднимает груз массой 300 кг на высоту 3 м за 10 с. Какова мощность лебёдки?
Ответы
Механическая работа. Мощность
Оценка
Источник
Òåðìèí «ðàáîòà» áûë ââåäåí â ôèçèêó â 1826 ã. ôðàíöóçñêèì ó÷åíûì Æ. Ïîíñåëå. Åñëè â îáûäåííîé æèçíè ðàáîòîé íàçûâàþò ëèøü òðóä ÷åëîâåêà, òî â ôèçèêå è, â ÷àñòíîñòè, â ìåõàíèêå ïðèíÿòî ñ÷èòàòü, ÷òî ðàáîòó ñîâåðøàåò ñèëà. Ôèçè÷åñêóþ âåëè÷èíó ðàáîòû îáû÷íî îáîçíà÷àþò áóêâîé À.
Ðàáîòà ñèëû — ýòî ìåðà äåéñòâèÿ ñèëû, çàâèñÿùàÿ îò åå ìîäóëÿ è íàïðàâëåíèÿ, à òàêæå îò ïåðåìåùåíèÿ òî÷êè ïðèëîæåíèÿ ñèëû. Äëÿ ïîñòîÿííîé ñèëû è ïðÿìîëèíåéíîãî ïåðåìåùåíèÿ ðàáîòà îïðåäåëÿåòñÿ ðàâåíñòâîì:
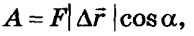
ãäå F — ñèëà, äåéñòâóþùàÿ íà òåëî,  — ïåðåìåùåíèå, α — óãîë ìåæäó ñèëîé è ïåðåìåùåíèåì.
— ïåðåìåùåíèå, α — óãîë ìåæäó ñèëîé è ïåðåìåùåíèåì.

Ðàáîòà ñèëû ðàâíà ïðîèçâåäåíèþ ìîäóëåé ñèëû è ïåðåìåùåíèÿ è êîñèíóñà óãëà ìåæäó íèìè, ò. å. ñêàëÿðíîìó ïðîèçâåäåíèþ âåêòîðîâ F è  .
.
Ðàáîòà — âåëè÷èíà ñêàëÿðíàÿ. Åñëè α < 90°, òî À > 0, à åñëè 90° < α < 180°, òî À < 0; åñëè æå α = 90°, òî À = 0. Òàê, ñèëà òÿæåñòè íå ñîâåðøàåò ðàáîòó ïðè ïåðåìåùåíèè òåëà ïî ãîðèçîíòàëüíîé ïëîñêîñòè. Òàêæå ïðè äâèæåíèè ñïóòíèêà ïî êðóãîâîé îðáèòå ñèëà òÿãîòåíèÿ íå ñîâåðøàåò ðàáîòó.
Ïðè äåéñòâèè íà òåëî íåñêîëüêèõ ñèë ïîëíàÿ ðàáîòà (ñóììà ðàáîò âñåõ ñèë) ðàâíà ðàáîòå ðåçóëüòèðóþùåé ñèëû.
Åäèíèöåé ðàáîòû â ÑÈ ÿâëÿåòñÿ äæîóëü (1 Äæ). 1 Äæ — ýòî ðàáîòà, êîòîðóþ ñîâåðøàåò ñèëà â 1 Í íà ïóòè â 1 ì â íàïðàâëåíèè äåéñòâèÿ ýòîé ñèëû. Ýòà åäèíèöà íàçâàíà â ÷åñòü àíãëèéñêîãî ó÷åíîãî Äæ. Äæîóëÿ (1818-1889): 1 Äæ= 1 Í · ì. ×àñòî ïðèìåíÿþòñÿ òàêæå êèëîäæîóëè è ìèëëèäæîóëè: 1 êÄæ = 1 000 Äæ, 1 ìÄæ = 0,001 Äæ.
Êàëüêóëÿòîðû ïî ôèçèêå | |
| Ðåøåíèå çàäà÷ ïî ôèçèêå, ïîäãîòîâêà ê ÝÃÅ è ÃÈÀ, ìåõàíèêà òåðìîäèíàìèêà è äð. | |
| Êàëüêóëÿòîðû ïî ôèçèêå | |
Ôèçèêà. Ðàáîòà. | |
| Ðàáîòà â òåðìîäèíàìèêå; ñèëû òÿæåñòè, òðåíèÿ, óïðóãîñòè; ðàáîòà ýëåêòðè÷åñêîãî òîêà, âûõîäà ýëåêòðîíîâ; çàêîí Äæîóëÿ-Ëåíöà | |
| Ôèçèêà. Ðàáîòà. | |
Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ôèçèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ðàáîòà âûõîäà ýëåêòðîíîâ. | |
| Òàáëèöà ðàáîòû âûõîäà òàêèõ ýëåêòðîíîâ êàê: áàðèé, âîëüôðàì, ãåðìàíèé, çîëîòî, êàëüöèé, ìîëèáäåí, íèêåëü è òä. | |
| Ðàáîòà âûõîäà ýëåêòðîíîâ. | |
Ðàáîòà âûõîäà ýëåêòðîíîâ èç ìåòàëëîâ | |
| Òàáëèöà ðàáîòû âûõîäà ýëåêòðîíîâ èç ìåòàëëîâ òàêèõ êàê: àëþìèíèé, âîëüôðàì, æåëåçî, ìåäü, íèêåëü, îëîâî, ïëàòèíà è òä. | |
| Ðàáîòà âûõîäà ýëåêòðîíîâ èç ìåòàëëîâ | |
Ðàáîòà ñèëû òðåíèÿ. | |
| Ñèëà òðåíèÿ íàïðàâëåíà ïðîòèâîïîëîæíî ïåðåìåùåíèþ Δx è ñîñòàâëÿåò ñ íèì óãîë 180º, ïîýòîìó ðàáîòà ñèëû òðåíèÿ îòðèöàòåëüíà: . | |
| Ðàáîòà ñèëû òðåíèÿ. | |
Источник
Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
Используемые обозначения[править | править код]
Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).
Определение[править | править код]
Работа силы, приложенной к материальной точке[править | править код]
Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:
Здесь точкой обозначено скалярное произведение, — вектор перемещения; подразумевается, что действующая сила постоянна в течение времени, за которое вычисляется работа.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[2]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[3], интеграл определяется[4] следующим образом:
,
где и — радиус-векторы начального и конечного положения тела соответственно.
- Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.
Работа сил, приложенных к системе материальных точек[править | править код]
Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).
Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия[править | править код]
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если — полная работа, совершённая над частицей, определяемая как сумма работ, совершённых приложенными к частице силами, то она выражается как:
где называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как[5]:
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия[править | править код]
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая, что
Если все силы, действующие на частицу, консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:
.
Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,
,
является постоянной во времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике[править | править код]
В термодинамике работа, совершённая газом при расширении[6], рассчитывается как интеграл давления по объёму:
Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.
Работа силы в теоретической механике[править | править код]
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, , и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).
Величина , называется элементарной работой силы на участке и принимается за приближённое значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .
Таким образом, если обозначить эту работу буквой , то, в силу данного определения,
,
следовательно,
(1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим
Размерность и единицы[править | править код]
Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг
1 Дж = 1 кг·м²/с² = 1 Н·м
1 эрг = 1 г·см²/с² = 1 дин·см
1 эрг = 10−7Дж
См. также[править | править код]
- Закон сохранения энергии
- Теорема о кинетической энергии системы
- Механические приложения криволинейных интегралов
Примечания[править | править код]
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях суммируется, что и даёт в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература[править | править код]
- История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
- Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
- Льоцци М. История физики. М.: Мир, 1970.
- Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
- Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.
Источник

