Что такое полезная работа совершаемая механизмом

Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.

Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.

Определение и расшифровка КПД

Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.

Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».

Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.

В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.

Полезная работа

При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.

В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.

Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.

Итог:

• Затрачиваемая работа Aз всегда больше полезной Ап.
• Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
• Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД

Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.

Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.

В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.

Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.

Итак, формула КПД:

Ƞ=А/Q, где

• A — полезная работа, которую выполняет система.
• Q — энергия, которую потребляет система.

Применение в разных сферах физики

Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.

Рассмотрим несколько из примеров процессов с наличием КПД.

К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.

Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.

Видео

Это видео поможет вам понять, что такое КПД.

Задача №1

К бруску прикрепили динамометр и переместили брусок на расстояние 30 см. Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).

Рис 1. К задаче №1

Прежде всего запишем краткое условие задачи и позаботимся, чтобы все данные были выражены в системе СИ (рис. 2).

Рис 2. Краткое условие задачи №1

Для вычисления работы воспользуемся формулой

Полное решение задачи выглядит так (рис. 3).

Рис 3. Полное решение задачи №1

Задача №2

Трактор перемещает платформу со скоростью 7,2 км/ч, развивая тяговое усилие в 25 кН. Какую работу совершит трактор за 10 мин (рис. 4)?

Рис 4. К задаче №2

Запишем краткое условие задачи и переведем все единицы измерения в систему СИ (рис. 5).

Рис 5. Краткое условие задачи №2

Для вычисления работы необходимо знать расстояние, пройденное телом. В условии задачи дана скорость движения трактора и время движения, поэтому воспользуемся формулой

которую подставим в выражение для работы  и получим рабочую формулу

Подстановка данных из условия задачи дает

Рис 6. Полное решение задачи №2

Задача №3

Найдем работу силы тяжести при падении грузика.

Для решения задачи нам потребуется линейка и сам грузик. Измерим высоту, с которой будет падать грузик. Получаем 1 м. Масса грузика написана на нем самом и равна 100 г. Поднимем грузик на указанную высоту и отпустим его.

Краткое условие задачи будет выглядеть так (рис. 7):

Рис 7. Краткое условие задачи №3

Для нахождения работы выразим силу тяжести через массу тела , и учтем, что расстояние, пройденное телом, равно высоте, с которой оно упало: .

Тогда

Подстановка чисел дает

Рис 8. Полное решение задачи №3

Теперь у нас есть представление о том, насколько велика работа в 1 джоуль. Такая работа совершается при падении грузика массой 100 г со стола высотой 1 м.

Переходим к решению более сложных задач.

Задача №4

Со дна реки глубиной 4 м поднимают камень объемом 0,6 м3 на поверхность. Плотность камня 2500 кг/м3, плотность воды 1000 кг/м3. Найти работу по подъему камня.

Для решения задачи необходимо не только записать краткое условие задачи, но и сделать схематический рисунок и показать силы, действующие на камень. Это сила тяги Fт (работу именно этой силы мы будем находить), сила тяжести mg и сила Архимеда Fa. Кроме того, покажем высоту, на которую сила тяги перемещает камень (рис. 9).

Рис 9. К решению задачи №4

Как видно из рисунка, искомая работа равна .

Для нахождения силы тяги воспользуемся условием равновесия тела: если оно неподвижно или движется с постоянной скоростью, то равнодействующая всех сил, приложенных к нему, равна нулю.

, откуда .

Массу камня выразим через плотность камня и его объем, а силу Архимеда – через плотность воды и объем погруженной части камня (в этом задаче он равен объему всего камня). Объем камня и ускорение выносим за скобки.

Остается подставить силу тяги в формулу для вычисления работы

Поскольку рабочая формула получилась более сложной, единицы измерения результата определим отдельно от расчета его численного значения.

Рис 10. Полное решение задачи №4

Задача №5

Поршень двигателя перемещается на 20 см под давлением 800 кПа. Определите работу, совершаемую двигателем за один ход поршня, если площадь поршня 150 см2 (рис. 11).

Рис 11. К задаче №5

Запишем краткое условие и выразим все единицы в системе СИ (рис. 12).

Рис. 12. Краткое условие задачи №5

В данной задаче работу выполняет сила давления газа в цилиндре двигателя. Для нахождения этой силы необходимо давление в цилиндре умножить на площадь поршня. Расстояние, пройденное поршнем, мы обозначили буквой l.

Единицы измерения результата:

Численное значение результата:

Рис 13. Полное решение задачи №5

Задача №6

Найти КПД (коэффициент полезного действия) наклонной плоскости (экспериментальная) (рис. 14).

Рис. 14. Груз поднимают вверх по наклонной плоскости

Поднимая груз по наклонной плоскости с помощью динамометра, измерим силу, которая для этого требуется. Она оказывается равной 2,2 Н. Расстояние, пройденное грузом вдоль плоскости, измеряем рулеткой. Оно составило 0,5 м. При этом груз поднялся над столом на высоту 20 см. Кроме того, известны масса бруска, равная 50 г, и общая масса трех поднимаемых грузов – 300 г.

Полученные опытные данные занесем в краткое условие задачи, выразим все величины в единицах системы СИ и сделаем схематический рисунок измерительной установки (рис. 15).

Рис 15. Краткое условие задачи №6

Коэффициентом полезного действия механизма называется физическая величина, равная отношению полезной работы, совершенной механизмом, к работе, затраченной для приведения его в действие.

КПД также обозначают греческой буквой η (эта) и часто выражают в процентах.

В нашем случае механизмом является наклонная плоскость.

Полезная работа – эта работа, которую нужно совершить, чтобы поднять тело на высоту h.

Затраченная работа совершается силой тяги, то есть силой упругости пружины динамометра.

Тогда КПД равен

Определяем единицы измерения КПД

Такой результат означает, что КПД является безразмерной величиной (просто число без единиц измерения).

Его числовое значение

Обратите внимание, что коэффициент полезного действия не может быть больше единицы, поскольку полезная работа всегда меньше затраченной. Если у вас получилось наоборот, значит, либо при измерениях, либо в ходе вычислений допущена ошибка.

Рис 16. Полное решение задачи №6

Задача №7

Трактор равномерно тянет плуг, прилагая силу в 10 кН. За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).

Рис 17. К условию задачи №7

Запись краткого условия и перевод величин в систему СИ будет выглядеть так (рис. 18):

Рис 18. Краткое условие задачи №7

Для нахождения мощности нужно работу, выполненную трактором, разделить на время ее выполнения. Работа вычисляется как произведение силы тяги трактора на пройденное трактором расстояние. Таким образом, получаем:

Рис 19. Полное решение задачи №7

Задача №8

Поезд массой 600 тонн равномерно движется со скоростью 36 км/ч. Определить развиваемую тепловозом мощность, если сила трения составляет 0,002 веса поезда.

Рис. 20. К условию задачи №8

Запишем краткое условие задачи, выразим величины в единицах системы СИ, сделаем рисунок, на котором покажем силу тяги тепловоза и силу трения (рис. 21).

Рис. 21. Краткое условие задачи №8

Поскольку по условию задачи скорость поезда не изменяется и равна 36 км/ч, сила тяги равна силе трения  Вес в случае движения с постоянной скоростью равен силе тяжести  Тогда сила тяги равна

Для вычисления мощности воспользуемся формулой  откуда

Подстановка данных из условия дает

Рис. 22. Полное решение задачи №8

Список литературы

1. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А.В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

Домашнее задание

1. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов №675–683, 706–712.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Единая коллекция Цифровых Образовательных Ресурсов (Источник).
2. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.

Что такое работа в физике – определение и формула

Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию. 

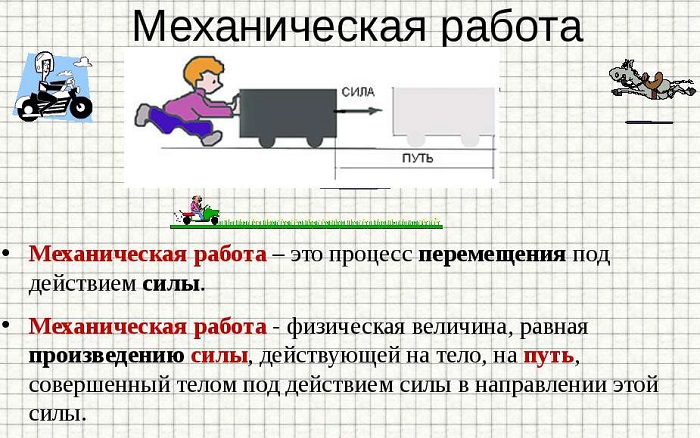
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:

A = F * S

В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:

A = F * S * cosA

В чем измеряется работа

Физические единицы, в которых выражается механическая работа, – Джоули. 

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах. 

Работа силы трения

При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной. 

Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.

Положительная и отрицательная работа

Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости. 

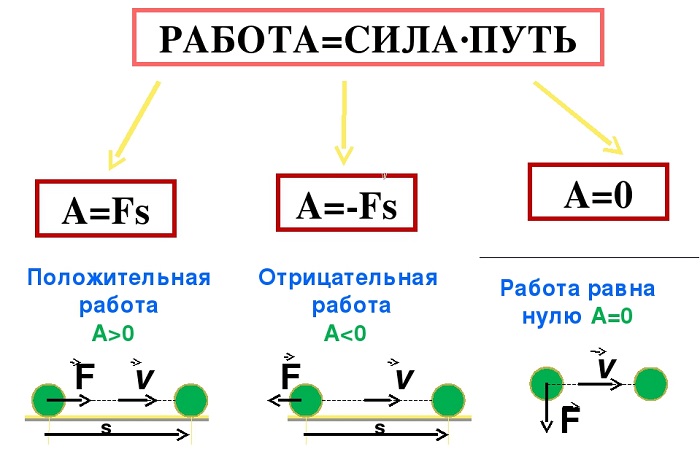
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей. 

Полезная или затраченная работа

У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле. 

Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:

КПД = А полезная / А затраченная,

и выражается в процентах. КПД всегда меньше 100.

Мощность

Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:

Р = A / t

В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.

Однако при равномерном движении можно использовать и другую формулу:

Р = F * v

Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.

Примеры решения задач

Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1

Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.

Решение:

Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.

При помощи простой математики найдем числовой ответ:

A = 50 м * 10 кг * 10 Н/кг;

A = 5000 Дж.

Ответ: 5000 Дж.

Впрочем, не всегда речь идет о силе тяжести.

Задача 2

Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.

Решение:

Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.

Далее при помощи элементарных вычислений рассчитаем ответ:

A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.

Ответ: 0,4 Дж.

Но во всех задачах по данной теме траектория движения тела прямая.

Задача 3

Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.

Решение:

В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.

Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.

Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).

В таком случае:

F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.

Ответ: 5308 Н.

В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.

Задача 4

Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.

Решение:

На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы. 

Запишем условие в более наглядном виде.

Дано:

m = 2500 кг;

F = 10000 H;

t = 10 с;

КПД = 30%;

угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);

V – ?

Выведение формулы:

Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).

A1 = mg;

A2 = P * t / КПД.

То есть mg = P * t / КПД.

Шаг 2. P = F * V * cosA.

Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.

V = (m * g * КПД) / (F * t * cosA).

Числовое решение:

V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);

V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);

V = 7500 / 50000;

V = 0,15 м/с.

Ответ: 0,15 м/с.