Что такое вредная и полезная инерция
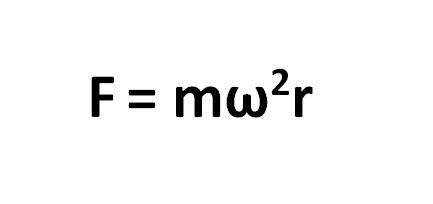
Ине́рция (от лат. inertia — покой, бездеятельность, постоянство, неизменность) — свойство тела оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие внешних воздействий[1][2], а также препятствовать изменению своей скорости (как по модулю, так и по направлению[3]) при наличии внешних сил за счёт своей инертной массы.
Понятию «инерция» синонимично одно из значений понятия инертность[1] (другие значения последнего не относятся к физике).
Количественно соотношение между воздействием на тело и изменением его движения даётся формулой второго закона Ньютона[4]:
.
Здесь — сила, действующая на тело, — инертная масса, — скорость тела.
С понятием инерции связано понятие инерциальных систем отсчёта.
Формулировка[править | править код]
Существование инерциальных систем отсчёта в классической механике постулируется первым законом Нью́тона, который также называется зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:
Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Современная, более точная, формулировка закона:
Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными.
В неинерциальных системах отсчёта закон инерции не выполняется. Тем не менее движение тел в неинерциальных системах отсчёта можно описывать теми же уравнениями движения, что и в инерциальных, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать силы инерции[5][6].
История[править | править код]
Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте[7]:
Однако в другом труде «Механика», приписываемом Аристотелю, утверждается[8]:
Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.
Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку «аристотелевской физики». В своем труде «Беседы о двух новых науках» Галилей писал[8]:
Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то при движении по горизонтальной плоскости у тела нет причин ускоряться или замедляться — и оно должно пребывать в состоянии равномерного движения или покоя.
Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считали Аристотель и его последователи. Это открытие Галилея вошло в науку как закон инерции. Однако, Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В 1638 году итальянец Балиани уточнил закон инерции, указав, что при полном отсутствии внешних воздействий естественной траекторией движения тела является прямая. В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.
Смежные понятия[править | править код]
Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведённой в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.
Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (другими примерами абстрактной модели служат абсолютно твёрдое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами, и соответствие реально наблюдаемого движения тел в таких системах результатам расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика.
Инертная масса — мера инертности тела в физике, показатель того, в большей или меньшей степени данное тело будет препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии внешних сил. Инертная масса фигурирует в выражении второго закона Ньютона, являющегося важнейшим законом классической механики.
См. также[править | править код]
- Законы Ньютона
- Сила инерции
- Момент инерции
- Принцип Маха
- Механика
- Гистерезис
- Теория импетуса
- Инертная масса
Примечания[править | править код]
- ↑ 1 2 3 Инерция // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Т.И.Трофимов. Физика. — Москва: «Академия», 2012.
- ↑ Коноплёва Н. П. Об эволюции понятия инерции (Ньютон, Мах, Эйнштейн) // Эйнштейновский сборник 1975-1976. — М., Наука, 1978. — с. 216-244
- ↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — С. 118—119.
- ↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 292
- ↑ Физика (Аристотель)/Книга 4/Глава 8
- ↑ 1 2 Эйнштейн А., Инфельд Л. Эволюция физики. — М.: Наука, 1965. — С. 10-12.
Литература[править | править код]
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Кокарев С. С. Три лекции о законах Ньютона. Ярославль. Сб. трудов РНОЦ Логос, вып. 1, 45-72, 2006.
Ссылки новых исследований:
- Masreliez C. J., Motion, Inertia and Special Relativity — a Novel Perspective, Physica Scripta (2006).
- Masreliez C. J., On the origin of inertial force, Apeiron (2006).
- Masreliez, C J; Dynamic incremental scale transition with application to physics and cosmology, Physica Scripta (2007).
Источник
Из повседневного опыта мы можем подтвердить следующее умозаключение: скорость и направление движения тела могут меняться лишь во время его взаимодействия с другим телом. Это порождает явление инерции, о котором мы и поговорим в этой статье.
Что такое инерция? Пример жизненных наблюдений
Рассмотрим случаи, когда какое-нибудь тело на начальном этапе эксперимента уже пребывает в движении. Позже мы увидим, что уменьшение скорости и остановка тела не могут происходить самовольно, ведь причиной тому является действие на него другого тела.
Вы, наверное, не единожды наблюдали, как пассажиры, которые едут в транспорте, вдруг наклоняются вперед во время торможения или прижимаются на бок на крутом повороте. Почему? Объясним далее. Когда, к примеру, спортсмены пробегают определенную дистанцию, они пытаются развить максимальную скорость. Пробежав финишную черту, уже можно и не бежать, однако нельзя резко остановиться, а поэтому спортсмен пробегает еще несколько метров, то есть совершает движение по инерции.

Из вышеперечисленных примеров можно сделать вывод, что все тела имеют особенность сохранять скорость и направление движения, не будучи в состоянии при этом мгновенно их изменить впоследствии действия иного тела. Можно предположить, что при отсутствии внешнего действия тело сохранит и скорость, и направление движения как угодно долго. Итак, что такое инерция? Это явление сохранения скорости движения тела при отсутствии воздействия на него других тел.
Открытие инерции
Такое свойство тел открыл итальянский ученый Галилео Галилей. На основе своих экспериментов и рассуждений он утверждал: ежели тело не взаимодействует с иными телами, то оно либо пребывает в состоянии спокойствия, либо движется прямолинейно и равномерно. Его открытия вошли в науку как Закон инерции, однако более детально сформулировал его Рене Декарт, а уж Исаак Ньютон внедрил в свою систему законов.
Интересный факт: инерция, определение которой привел нам Галилей, рассматривалась еще в Древней Греции Аристотелем, но из-за недостаточного развития науки, точной формулировки приведено не было. Первый закон Ньютона гласит: существуют такие
системы отсчета, относительно которых тело, которое движется поступательно, сохраняет свою скорость постоянной, если на него не действуют иные тела. Формула инерции в едином и обобщенном виде отсутствует, но ниже мы приведем множество иных формул, раскрывающих ее особенности.

Инертность тел
Все мы знаем, что скорость человека, автомобиля, поезда, корабля или других тел увеличивается постепенно, когда они начинают двигаться. Все вы видели запуск ракет по телевизору или взлет самолетов в аэропорту — они увеличивают скорость не рывками, а постепенно. Наблюдения, а также повседневная практика говорят о том, что все тела имеют общую особенность: скорость движения тел в процессе их взаимодействия меняется постепенно, а поэтому для их изменения необходимо некоторое время. Эта особенность тел получила название инертности.
Все тела инертны, но не у всех инертность одинакова. Из двух взаимодействующих тел она будет выше у того, которое обретет меньшее ускорение. Так, к примеру, при выстреле ружье приобретает меньшее ускорение, чем патрон. При взаимном отталкивании взрослого конькобежца и ребенка взрослый получает меньшее ускорение, чем ребенок. Это свидетельствует о том, что инертность взрослого человека больше.
Для характеристики инертности тел ввели особенную величину — массу тела, ее принято обозначать буквой m. Дабы иметь возможность сравнивать массы различных тел, массу кого-нибудь из них необходимо учесть за единицу. Ее выбор может быть произвольным, однако она должна быть удобной для практического употребления. В системе СИ за единицу взяли массу специального эталона, изготовленного из твердого сплава платины и иридия. Она носит всем нам известное название — килограмм. Следует отметить, что инерция твердого тела бывает 2-х видов: поступательная и вращательная. В первом случае мерой инерции является масса, во втором — момент инерции, о котором мы поговорим позже.
Момент инерции
Так называют скалярную физическую величину. В системе СИ единицей измерения момента инерции является кг*м2. Обобщенная формула следующая:
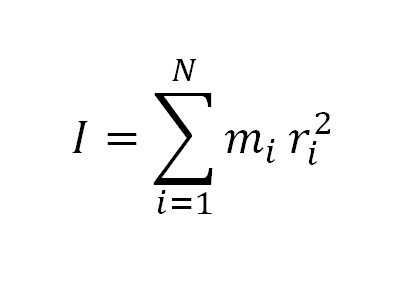
Здесь mi — это масса точек тела,ri — это расстояние от точек тела до оси z в пространственной системе координат. В словесной интерпретации можно сказать так: момент инерции определяется суммой произведений элементарных масс, умноженных на квадрат расстояния до базового множества.
Есть и другая формула, характеризующая определение момента инерции:
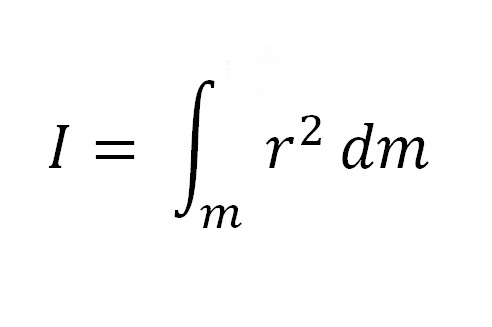
Здесь dm — масса элемента, r — расстояние от элемента dm до оси z. Словесно можно сформулировать так: момент инерции системы материальных точек или тела относительно полюса (точки) — это алгебраическая сумма произведения масс материальных точек, составляющих тело, на квадрат расстояния их до полюса 0.
Стоит упомянуть, что существует 2 вида моментов инерции — осевые и центробежные. Есть также такое понятие, как главные моменты инерции (ГМИ) (относительно главных осей). Как правило, они всегда различны между собой. Ныне можно рассчитать моменты инерции для многих тел (цилиндра, диска, шара, конуса, сферы и проч.), однако не будем углубляться в уточнение всех формул.
Системы отсчета
В 1-ом законе Ньютона шла речь о равномерном прямолинейном движении, которое можно рассматривать только в определенной системе отсчета. Даже приближенный анализ механических явлений показывает, что закон инерции выполняется далеко не во всех системах отсчета.
Рассмотрим простой эксперимент: положим мяч на горизонтальный столик в вагоне и понаблюдаем за его движением. Если поезд будет находиться в состоянии спокойствия относительно Земли, то и мяч сохранит спокойствие до тех пор, пока мы не подействуем на него иным телом (например, рукой). Следовательно, в системе отсчета, что связана с Землей, закон инерции выполняется.
Представим, что поезд будет ехать относительно Земли равномерно и прямолинейно. Тогда в системе отсчета, что связана с поездом, мяч сохранит состояние спокойствия, а в той, что связана с Землей, — состояние равномерного и прямолинейного движения. Следовательно, закон инерции выполняется не только в системе отсчета, связанной с Землей, но и во всех других, движущихся относительно Земли равномерно и прямолинейно.
Теперь представим, что поезд быстро набирает скорость либо круто поворачивает (во всех случаях он движется с ускорением относительно Земли). Тогда, как и раньше, мяч сохраняет равномерное и прямолинейное движение, которое он имел до начала ускорения поезда. Однако относительно поезда мяч сам по себе выходит из состояния спокойствия, хотя и нет тел, которые бы выводили его из него. Это значит, что в системе отсчета, связанной с ускорением движения поезда относительно Земли, закон инерции нарушается.
Итак, системы отсчета, в которых выполняется закон инерции, получили название инерциальных. А те, в которых не выполняется, — неинерциальных. Определить их просто: если тело движется равномерно и прямолинейно (в отдельных случаях — это спокойствие), то система инерциальная; если движение неравномерное — неинерциальная.
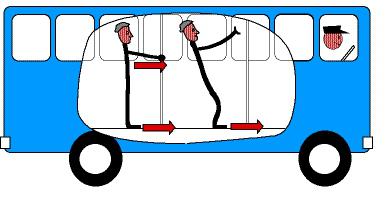
Сила инерции
Это довольно многозначное понятие, а поэтому попытаемся как можно более детально его рассмотреть. Приведем пример. Вы спокойно стоите в автобусе. Внезапно он начинает двигаться, а значит, набирает ускорение. Вы мимо воли отклонитесь назад. Но почему? Кто вас потянул? С точки зрения наблюдателя на Земле (инерциальная система отсчета) вы остаетесь на месте, при этом выполняется 1-ый закон Ньютона. С точки зрения наблюдателя в самом автобусе, вы начинаете двигаться назад, будто под какой-либо силой. На самом деле ваши ноги, которые связаны силами трения с полом автобуса, поехали вперед вместе с ним, а вам,
теряя равновесие, пришлось падать назад. Таким образом, для описания движения тела в неинерциальной системе отсчета необходимо вводить и учитывать дополнительные силы, что действуют со стороны связей тела с такой системой. Эти силы и есть силы инерции.
Необходимо учесть, что они фиктивны, ибо нет ни единого тела либо поля, под действием которого вы начали двигаться в автобусе. Законы Ньютона на силы инерции не распространяются, однако их использование наряду с «настоящими» силами позволяет описывать движение у произвольных неинерциальных систем отсчета при помощи различных инструментов. В этом состоит весь смысл ввода сил инерции.
Итак, теперь вы знаете, что такое инерция, момент инерции и инерциальные системы, силы инерции. Двигаемся далее.
Поступательное движение систем
Пусть на некое тело, находящееся в неинерциальной системе отсчета, движущееся с ускорением а0относительно инерциальной, действует сила F. Для такой неинерциальной системы уравнение-аналог второго закона Ньютона имеет вид:
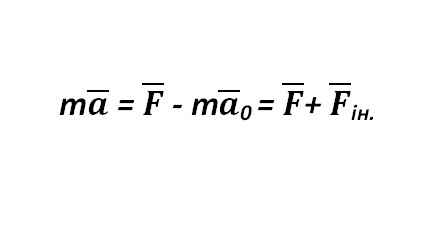
Где а0 – это ускорение тела с массой m, что вызвано действием силы F относительно неинерциальной системы отсчета; Fін — сила инерции. Сила F в правой части является «настоящей» в том понимании, что это результирующая взаимодействия тел, зависящая только от разности координат и скоростей взаимодействующих материальных точек, которые не меняются при переходе от одной системы отсчета к другой, движущейся поступательно. Поэтому не меняется и сила F. Она инвариантна относительно такого перехода. А вот Fін возникаетне по причине взаимодействия тел, а из-за ускоренного движения системы отсчета, из-за чего она меняется при переходе к другой ускоренной системе, поэтому не является инвариантной.
Центробежная сила инерции
Рассмотрим поведение тел в неинерциальной системе отсчета. XOY вращается относительно инерциальной системы, коей будем считать Землю, с постоянной угловой скоростью ω. Примером может послужить система на рисунке ниже.
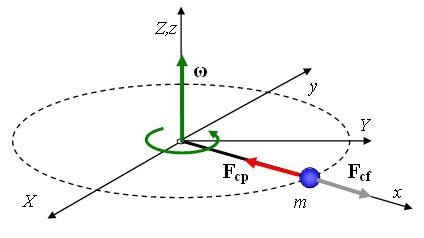
Выше изображен диск, где закреплен радиально направленный стержень, а также надет синий шарик, «привязанный» к оси диска эластичной веревкой. Пока диск не вращается, веревка не деформируется. Однако при раскручивании диска шарик понемногу растягивает веревку до тех пор, пока сила упругости Fср не станет такой, что равна произведению массы шарика m на ее нормальное ускорение aп = -ω2R, то есть Fср = -mω2R, где R — это радиус круга, который описывает шарик при вращении вокруг системы.
Ежели угловая скорость ω диска останется постоянной, то и шарик прекратит движение относительно оси OX. В этом случае относительно системы отсчета XOY, которая связана с диском, шарик будет находиться в состоянии спокойствия. Это объяснится тем, что в этой системе, помимо силы Fср, на шарик действует сила инерции Fcf,которая направлена вдоль радиуса от оси вращения диска. Сила, имеющая вид, как в формуле, представленной ниже, называется центробежной силой инерции. Возникать она может только во вращающихся системах отсчета.
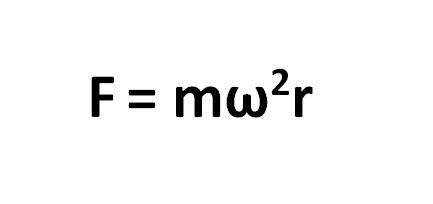
Сила Кориолиса
Оказывается, когда тела двигаются относительно вращающихся систем отсчета, на них, помимо центробежной силы инерции, действует еще одна сила — Кориолиса. Она всегда перпендикулярна к вектору скорости тела V, а это означает, что она не выполняет никакой работы над этим телом. Подчеркнем, что сила Кориолиса проявляет себя лишь тогда, когда тело движется относительно неинерциальной системы отсчета, которая осуществляет вращение. Ее формула выглядит следующим образом:
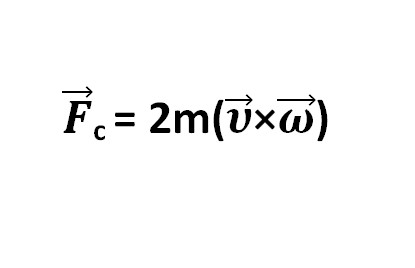
Поскольку выражение (v*ω) является векторным произведением приведенных в скобках векторов, то можно прийти к выводу, что направление силы Кориолиса определяется правилом буравчика по отношению к ним.Ее модуль равен:

Здесь Ө – это угол между векторами v и ω.
В заключение
Инерция — это удивительное явление, которое ежедневно преследует каждого человека сотни раз, пусть мы и сами не замечаем этого. Думаем, что статья дала вам важные ответы на вопросы о том, что такое инерция, что такое сила и моменты инерции, кто открыл явление инерции.Уверены, вам было интересно.
Источник

