Для упрощения вычислений полезно помнить что
ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 5 класс
- Математика
- Никольский
- Упражнение 97

Назад к содержанию
Условие
Для упрощения вычислений полезно помнить, что
2 * 5 = 10;
4 * 25 = 100;
8 * 125 = 1000.
Пользуясь этими равенствами, вычислите устно:
а) 3 * 2 * 5;
б) 2 * 7 * 5;
в) 4 * 9 * 25;
г) 7 * 25 * 4;
д) 125 * 7 * 8;
е) 12 * 8 * 125;
ж) 2 * 17 * 5;
з) 16 * 25 * 4;
и) 13 * 125 * 8.
Решение 1

Решение 2
Решение 3
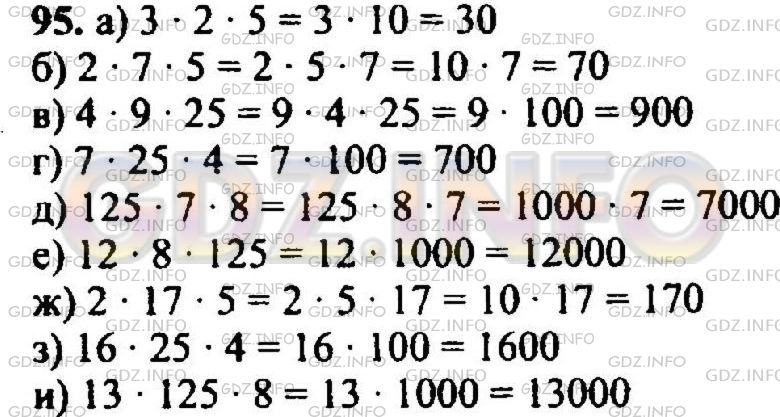
Другие задачи из этого учебника
- 94
- 95
- 96
- 97
- 98
- 99
- 100
Поиск в решебнике
Популярные решебники
 ГДЗ по Математике за 5 класс: Виленкин Н.Я
ГДЗ по Математике за 5 класс: Виленкин Н.Я
Издатель: Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. 2013г.
 ГДЗ по Математике за 5 класс: Мерзляк А.Г.
ГДЗ по Математике за 5 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.
 ГДЗ по Математике за 5 класс: Никольский С.М.
ГДЗ по Математике за 5 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.
 ГДЗ по Математике за 5 класс: Дорофеев Г.В.
ГДЗ по Математике за 5 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017г.
 ГДЗ по Математике за 5 класс: Зубарева, Мордкович
ГДЗ по Математике за 5 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2013г.
Источник
Математика
6 класс
Урок № 31
Действия с суммами нескольких слагаемых
Перечень рассматриваемых вопросов:
- Понятие суммы нескольких слагаемых для выражений вида – 3 + 6 – 1.
- Применение правил суммы для упрощения вычислений.
- Научимся упрощать рационально выражения вида – 3 + 6 – 1.
Тезаурус
Таким образом, сумма целых чисел a и b есть целое число c, отстоящее в ряду целых чисел от a на |b| чисел вправо, если b> 0, и влево, если b < 0. При этом числа a и b называют слагаемыми.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Рассмотрим выражение
– 3 + 6 – 1
Такое выражение часто называют суммой, поэтому, запишем его в виде суммы
– 3 + 6 + (– 1)
Известно, что для упрощения записи суммы и разности «плюсы» можно опускать, поэтому следующие равенства будут верны.
+ (– 3) = – 3
+ (+ 6) = + 6
+ (3 + 6) = 3 + 6
+ (6 – 1) = 6 – 1
+ (– 3 + 6 – 1) = – 3 + 6 – 1
Такие же результаты можно получить,используя равенства:
+ a = (+1) ∙ a
Например,
+ (– 3 + 6 – 1) = (+1) ∙ (– 3 + 6 – 1) =
= (+ 1) ∙ (– 3) + (+ 1) ∙ (+ 6) + (+ 1) ∙ (– 1) =
= – 3 + 6 – 1
Итак, верно равенство
+ (– 3 + 6 – 1) = – 3 + 6 – 1
В левой части этого равенства слагаемые заключены в скобки, а в правой – скобки раскрыты.
Нам уже известно, как раскрыть скобки, перед которыми стоит знак «+» или знак «–».
Но встречаются суммы, в которых знаки «+» и «–», стоящие перед скобками, обозначают действия сложения и вычитания.
Правила раскрытия скобок в этом случае тоже будут выполняться.
а + (b – с) = а + b – с
а, b и с – целые числа.
Верны равенства:
а + (b – с) = а + b – с
и
а – (b – с) = а – b + с, где а, b и с – целые числа
Докажем эти равенства
а + (b – с) = а + b – с
Доказательство
а + (b – с) = а + (b + (– с)) = а + b + (– с) = а + b – с
Докажем следующее равенство
а – (b – с) = а – b + с
Доказательство
а – (b – с) = а +(– (b – с)) = а +(– b + с) = а – b + с
Примеры
8 + (6 – 3) = 8 + 6 – 3
8 – (5 – 4) = 8 – 5 + 4
Итак, при вычислении суммы
При вычислении суммы нескольких слагаемых используют правила раскрытия скобок, заключения в скобки и законы сложения.
Вычислить значение суммы нескольких слагаемых (1 способ).
68 – 79 + 22 – 31
Решение
68 – 79 + 22 – 31 = (68 + 22) + (– 79 – 31) =
= 90 + (– 110) = 90 – 110 = – 20
Вычислить значение суммы нескольких слагаемых (2 способ).
68 – 79 + 22 – 31
Решение
68 – 79 + 22 – 31 = (68 – 79) + (22 – 31) =– 11– 9 = – 20
Таким образом, на этом уроке мы сформулировали понятие суммы нескольких слагаемых для выражений вида
– 3 + 6 – 1
Рассмотрели, как
– применятьправила суммы для упрощения вычислений;
– упрощать рационально выражения вида– 3 + 6 – 1;
– применять правила действий с суммами нескольких слагаемых для упрощения вычислений.
Дополнительный материал
Рассмотрим упрощение алгебраических выражений, в которых присутствуют действия с суммами нескольких слагаемых.
Найти значение x, при котором равенство верно:
100 – (5 + 100 – х) = 20
В левой части равенства раскроемскобки, перед которыми стоит знак «минус», поменяв все знаки слагаемых на противоположные.
100 – 5 – 100 + х = 20
Пользуясь переместительным и сочетательными законами сложения получаем
100 – 5 – 100 + х = 20
– 5 + х = 20
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, то есть
х = 20 – (– 5)
х = 20 + 5
х = 25
Ответ: х = 25.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Какие законы представлены?
a ∙ (b + c) = a ∙ b + a∙ c
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Варианты ответов:
Сочетательный закон умножения
Переместительный закон умножения
Распределительный закон сложения
Распределительный закон умножения
Для ответа на вопрос задания, обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
- Распределительный закон сложения
- Сочетательный закон умножения
Тип 2. Вставьте в текст нужные слова.
При вычислении суммы нескольких … используют … скобок, заключения в скобки и….
Варианты ответов:
слагаемых
правила раскрытия
законы сложения
законы умножения
свойства умножения
Для ответа на вопрос задания, обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
При вычислении суммы нескольких слагаемых используют правила раскрытия скобок, заключения в скобки и законы сложения.
Источник
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
умножить на 4 — это дважды умножить на 2;
умножить на 6 — это значит умножить на 2, а потом на 3;
умножить на 8 — это трижды умножить на 2;
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
разделить на 4 — это дважды разделить на 2;
разделить на 6 — это сначала разделить на 2, а потом на 3;
разделить на 8 — это трижды разделить на 2;
разделить на 9 — это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
Источник
Добрый день, дорогие гости!
Сможете ли Вы перемножить два числа, к примеру 255 на 316 не зная таблицы умножения, или проще, хотя бы 32 на 17? Скорее, придется задуматься над этими примерами, а в данной статье я расскажу и покажу как в несколько совершенно простых действий найти решение, и знания таблицы умножения Вам вообще не понадобятся…
Уверен, что 15 минут практики, и вы будете в восторге! Главное, чуть-чуть довести до автоматизма, так как эти приемы не похожи на наши школьные
Старинная книга по арифметике
Признаюсь, когда нет под рукой калькулятора, я сам применяю данную систему вычисления без всякого умножения в столбик. Названий у нее очень много «русско крестьянский метод», «древнеегипетский», «крестьянское умножение» и т.п.
Метод основан на многократном удвоение и делении на два — двух множителей, к примеру у нас есть два числа Х и Y, мы Х удваиваем, а Y делим пополам! Согласитесь, что при таком подходе результат произведения никогда не изменится.
Согласны ли вы, что 32*17, это одно и то же, что 16*34? Здесь мы 32 разделили на 2, а 17 удвоили. Далее 16*34 есть не что иное, как 8*68, далее 4*136, затем 2*272 и ответ 544! Без столбиков и без калькуляторов.
Для простоты записывается так:
Проще говоря, деление на два продолжается до тех пор, пока мы не получим значение первого множителя, равное 1.
Если у нас задача перемножить 45*64, для простоты, чтобы не производить вычисление с нечетным числом мы меняем местами множители и решаем:
64*45, 32*90, 16*180, 8*360, 4*720, 2*1440, 1*2880 = 2880 !!!
Теперь о нечетных числах
Древнее правило гласит, что при произведении нечетного числа на любое число, требуется от первого множителя откинуть единицу, а остаток разделить на 2, но к последнему итоговому числу добавить числа, которые получались в процессе вычисления и стоят в столбце напротив нечетных (сложно звучит, но на примере проще простого):
Предыдущий пример 45*64, но начинаем вычислять не меняя множители.
Теперь смотрите, логично, что часть чисел мы растеряли по пути, так как целых три раза откидывали единицу у первого множителя. Поэтому правило и гласит, что к результату 2048 нам нужно добавить те числа, которые стоят напротив нечетного первого множителя:
Друзья, в реальности, такой метод занимает очень мало времени, попробуйте из головы взять любой пример и произвести систему вычислений по данному методу.
И думаю, нам следовало бы внимательнее относиться к древней арифметике, ведь применяемые системы счёта упрощают жизнь. У меня на канале обязательно будут подобные статьи, которые упрощают алгоритмы различных расчетов в разы. Ведь согласитесь, что вычисления, которые вы ранее не могли сделать без карандаша и листа бумаги, могут быть доступны вам — в уме!
Я очень надеюсь, что статья Вам понравилась, и более того, стала полезна в части применения в жизненных ситуациях!
Читайте также не менее интересную статью о математической зависимости между старославянскими мерами длины: Между старинными мерами длины найдена математическая зависимость (верста, пядь, сажень, аршин и т.д.)
И еще несколько публикаций, которые Вам могут быть интересны:
Какую площадь займет все население планеты, собравшись плечом к плечу? Удивитесь, но этот участок можно объехать за 1 час
Как измерить ширину реки с берега не переплывая? (2 простых и реальных способа)
Источник


