Фигуры из кусочков квадрата к числу полезных

Функция
[x]
равна наибольшему целому числу,
превосходящемуx
(x
– любое действительное число). Например: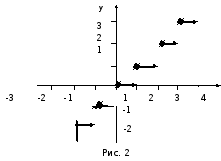

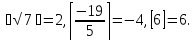
Функция
[x]
имеет «точки разрыва»: при целых
значениях x
она «изменяется скачком».

На
рис.2 дан график этой функции, причем
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки), а правый – не принадлежит.

Попробуйте
доказать,
что если каноническое разложение числа
n!
есть
,
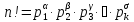то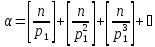

Аналогичные
формулы имеют место для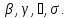

Зная
это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть
.
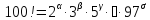Тогда

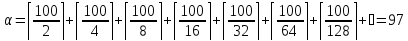и
.

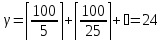Следовательно,
100! Делится на
,
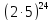т.е. оканчивается двадцатью четырьмя
нулями.

Фигуры из кусочков квадрата

К
числу полезных и увлекательных
развлечений относится составление
фигур из семи кусочков квадрата,
разрезанного в соответствии с рис.3,
(а), причем при составлении заданных
фигур должны быть использованы все
семь кусочков, и они должны налегать,
даже частично, друг на друга.

На
рис. 4 приведены симметричные фигуры1.
Попробуйте сложить эти фигуры из частей
квадрата, изображенного на рис. 3, (а).

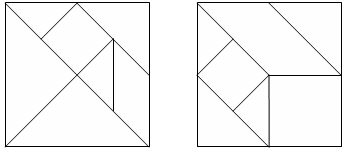
(а) (b)

Рис.3

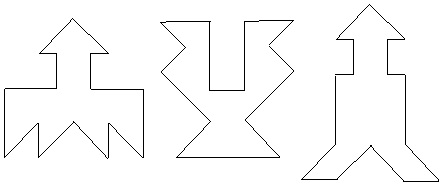
Рис.
4

Из
этих же чертежей можно складывать и
многие другие фигуры (например,
изображения различных предметов,
животных и т.п.).

Менее
распространенным вариантом игры
является составление фигур из кусочков
квадрата, изображенного на рис. 3, (b).

Магические квадраты

Магические
квадрат «n2-квадратом»
назовем
квадрат, разделенный на n2
клеток,
заполненных первыми n2
натуральными
числами так, что суммы чисел, стоящих
в любом горизонтальном или вертикальном
ряду, а также на любой из диагоналей
квадрата, равны одному и тому же числу

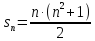
Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном и вертикальном
ряду, то квадрат называется полумагическим.

Магический
42
–квадрат назван именем Дюрера, математика
и художника XVIвека,
изображавшего квадрат на известной
картине «Меланхолия».

Кстати,
два нижних средних числа этого квадрата
образуют число 1514-дату создания картины.

Существует
лишь восемь девятиклеточных
магических квадратов.
Два
из них, являющиеся зеркальным изображением
друг друга, приведены на рисунке;
остальные шесть могут быть получены
из этих квадратов вращение их вокруг
центра на 90°, 180°, 270°

2.
Нетрудно полностью исследовать вопрос
о магических квадратов при n=3

Действительно,S3
= 15 , и существует лишь восемь способов
представления числа 15 в виде суммы
различных чисел (от единицы до девяти):

15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6

Заметим,
что каждое из чисел 1, 3, 7, 9 входит в две,
а каждое из чисел 2, 4, 6, 8 – в три указанные
суммы и лишь число 5 входит в четыре
суммы. С другой стороны, из восьми
трехклеточных рядов: трех горизонтальных,
трех вертикальных и двух диагональных
– через каждую из угловых клеток
квадрата проходит по три, через
центральную клетку по четыре и через
каждую из остальных клеток по два ряда.
Следовательно, число 5 должно обязательно
стоять в центральной клетке, числа 2,
4, 6, 8 – в угловых клетках, а числа 1, 3, 7,
9 – в остальных клетках квадрата.

Функция[х]
равна
наибольшему целому числу, не превосходящему
х (х
—
любое действительное число). Например:
2,=
— 4 ,=
6.

Функция
[х]
имеет
«точки разрыва»: при целых значениях х
она «изменяется скачком».

На
рис. 2 дан график этой функции, причем
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки),а правый — не принадлежит.

Попробуйте
доказать, что если каноническое
разложение числаn!
есть

n!=
p1α
•
p2β•p3γ•…
•pkδ,
то
α =

+ …

Аналогичные
формулы имеют месть для β,
γ, …, δ.

Зная
то, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть 100!=.
Тогда

и
.

Следовательно,
100! делится на
,
т.е оканчивается двадцатью четырьмя
нулями.

Фигуры из кусочков квадрата

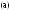
К
числу полезных и увлекательных развлечений
относится составление фигур из семи
кусочков квадрата, разрезанного в
соответствии с рис.3, (а), причем при
составлении заданных фигур должны быть
использованы все семь кусочков, и
они не должны налегать друг на друга.

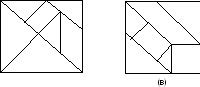
На
рис. 4 приведены симметричные фигуры.
Попробуйте сложить эти фигуры1из частей квадрата, изображенного на
рис.3, (а)

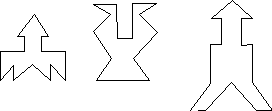
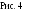
Из
этих же чертежей можно складывать и
многие другие фигуры (например, изображение
различных методов, животных и т.п.).

Менее
распространенным вариантом игры является
составление фигур из кусочков квадрата,
изображенного на рис. 3, (b).

Магические квадраты

Магическим
«n2-квадратом»
назовем квадрат, разделенный на n2
клеток,

заполненных
первыми n2
натуральными
числами так, что суммы чисел,стоящих в
любом горизонтально или вертикальном
ряду, а также на любой из диагоналей
квадрата, равны одному и тому же числу
.

Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном или вертикальном
ряду, то квадрат называется полумагическим.

Магический
42-квадрат имеет название Дюрера,
математика и художникаXVI
века, изобразившего квадрат на
известной картине «Меланхолия». Кстати,
два нижних средних числа этого квадрата
образуют число 1514-дату создания картины.

Существует
лишь восемь девятиклеточных магических
квадратов.Два из них, являющиеся
зеркальным изображением друг друга,
приведены на рисунке; остальные шесть
могут быть получены из этих квадратом
вращением их вокруг центра на 90о,
180о, 270о.

Приложение №1

1. Как
   известно, n!=(**)

   Если
   перебирать по порядку эти множители,
   то через каждые р1 «шагов» будут
   встречаться множители, кратные простому
   числу р1; число их равно,
   но из нихмножителей
   делятся на р12,—
   делятся на р13 и т.д.

   Следовательно,
   число множителей в равенстве (**), в
   состав которых множитель р1входит
   ровно один, два, три и т.д. Раза ,
   соответственно равно числам:

   и
   т.д.

Поэтому
α==

=+++…

Функция
[х]
равна наибольшему целому числу, не
превосходящему х
(х
–любое действительное число). Например:
,
,
[6]=6.

Функция
[x]
имеет «точки разрыва»: при целых
значениях х она «изменяется скачком».

На
рис.2 дан график этой функции, причём
левый конец каждого из горизонтальных
отрезков принадлежит графику (жирные
точки), а правый – не принадлежит.

Попробуйте
доказать,
что если каноническое разложение числаn!
есть

=
, то α =

Аналогичные
формулы имеют место для β,γ,…,δ.

Зная
это, легко определить, например, сколькими
нулями оканчивается число 100! Действительно,
пусть 100!
=
···…·97δ.
Тогда

и
γ=

Следовательно,
100! делится на (2·5)24,
т.е. оканчивается двадцатью четырьмя
нулями.

Фигуры из кусочков квадрата

К
числу полезных и увлекательных
развлечений относится составление
фигур из семи кусочков квадрата,
разрезанного в соответствии с рис.3,
(а), причём при составлении заданных
фигур должны быть использованы все
семь кусочков, и они не должны налегать,
даже частично, друг на друга.

На
рис.4 приведены симметричные фигуры1.
Попробуйте сложить эти фигуры из частей
квадрата, изображённого на рис.3,(а).

Рис.4

Из
этих чертежей можно складывать и многие
другие фигуры (например, изображения
различных предметов, животных и т.п.).

Менее
распространённым вариантом игры
является составление фигур из кусочков
квадрата, изображённого на рис. 3,(b).

Магические квадраты

Магическим
«n2-квадратом»
назовём квадрат, разделённый на n2
клеток, заполненных первыми n2
натуральными числами так, что суммы
чисел, стоящих в любом горизонтальном
или вертикальном ряду, а также на любой
из диагоналей квадрата, равны одному
и тому же числу .

Если
одинаковы лишь суммы чисел, стоящих в
любом горизонтальном и вертикальном
ряду, то квадрат называется полумагическим.

К
числу полезных и увлекательных развлечений
относится составление фигур из семи
кусочков квадрата, разрезанного в
соответствии с рисунком 1, (а), причем
при составлении заданных фигур должны
быть использованы все семь кусочков, и
они не должны налегать, даже частично,
друг на друга.

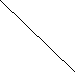
а)
Рисунок
1 b)

На
рисунке 2 приведены симметричные фигуры.
Попробуйте сложить эти фигуры из частей
квадрата, изображенного на рисунке 1,
(а).

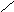
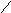
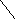
Рисунок
2

Задание 4. Создание титульного листа

А.П.Доморяд

Издательство
«Школьник»

Волгоград,2003
год.

2.
Введение в С++

Программа,
выводящая строку выдачи:

#include

main
()

{

cout
<< «Hello,
worldn»;
}

Строка
#include сообщает компилятору, чтобы он
включил стандартные возможности потока
ввода и вывода, находящиеся в файле
stream.h. Без этих описаний выражение cout <<
«Hello, worldn» не имело бы смысла. В
строке символ обратной косой , за которым
следует другой символ, обозначает один
специальный символ; в данном случае, n
является символом новой строки.Остальная
часть программы

main()
{ … }

определяет
функцию, названную main. Каждая
программа должна содержать функцию с
именем main, и работа программы начинается
с выполнения этой функции.

Первая
строка функции main() описывает целую
переменную inch. Ее значение считывается
с помощью операции >> («взять из»)
над стандартным потоком ввода cin. После
ее запуска ваш терминал может выглядеть
примерно так:

$
a.out

inches=12

12
in
= 30.48 cm

$

Часто
бывает полезно вставлять в программу
текст, который предназначается в качестве
комментария только для читающего
программу человека и игнорируется
компилятором в программе.

Символы
/* начинают комментарий, заканчивающийся
символами */. Символы // начинают
комментарий, который заканчивается в
конце строки, на которой они появились.

Каждое
имя и каждое выражение имеет тип,
определяющий операции, которые могут
над ними производиться. Например,
описание int inch; определяет, что inch имеет
тип int, то есть, inch является целой
переменной. Описание — это оператор,
который вводит имя в программе. Тип
определяет правильное использование
имени или выражения.

Основные
типы, наиболее непосредственно отвечающие
средствам аппаратного обеспечения,
такие:

char
short int long float double

Первые
четыре типа используются для представления
целых, последние

два
— для представления чисел с плавающей
точкой.

К
основному типу можно применять
прилагательное const. Это дает тип, имеющий
те же свойства, что и исходный тип, за
исключением того, что значение переменных
типа const не может изменяться после
инициализации.

const
float pi = 3.14;

const
char plus = ‘+’;

К
любой комбинации этих типов могут
применяться арифметические

операции:

А
также операции сравнения:

При
присваивании и арифметических операциях
C++ выполняет все

осмысленные
преобразования между основными типами,
чтобы их можно

было
сочетать без ограничений:

double
d = 1;

int
i = 1;

d
= d + i;

i
= d + i;

Поток
управления в программе задается с
помощью операторов , а описания
используются для введения в программе
имен переменных, констант и т.д. Заметьте,
что описания являются операторами,
поэтому они свободно могут сочетаться
с другими операторами.

В
C++ имеется большое число операций, и они
будут объясняться там, где (и если) это
потребуется. Следует учесть, что операции

Смысл
операции зависит от числа операндов;
унарное & является

операцией
взятия адреса, а бинарное & — это
операция логического И.

В
C++ есть операция присваивания =, а не
оператор присваивания,

как
в некоторых языках. Таким образом,
присваивание может

встречаться
в неожиданном контексте; например,
x=sqrt(a=3*x).

Например,

x[i+3]*=4
означает x[i+3]=x[i+3]*4, за исключением того
факта, что

выражение
x[i+3] вычисляется только один раз.

В
большинстве программ на C++ широко
применяются указатели.

Самый
обычный вид оператора — оператор
выражение. Он состоит из выражения, за
которым следует точка с запятой.

Простейшей
формой оператора является пустой
оператор: 
;

Заметьте,
что условие в операторе if должно быть
заключено в круглые скобки.

Оператор
switch производит сопоставление значения
с множеством констант.

Операторы
break применяются для выхода из оператора
switch.

Следующее
после while условие должно быть заключено
в круглые

скобки.

for
(int i=0; i<10; i++) q[i]=»p[i];»

Описание
— это оператор, вводящий имя в программе.
Оно может также инициализировать объект
с этим именем. Выполнение описания
означает, что когда поток управления
доходит до описания, вычисляется
инициализирующее выражение (инициализатор)
и производится инициализация. 

3.
Краткое знакомство со средой Visual
С++

Компилятор
VisualC++ содержит много новых инструментальных
средств и улучшенных возможностей.
Файлы рабочего пространства теперь
имеют расширение DSW(раньше использовалось
расширение MDP). Создаваемые проекты
записываются в файлы двух типов:
внутренние (DSP) и внешние (МАК). Файлы с
расширением DSP создаются при выборе
нового проекта или при открытии файла
проекта, созданного в ранней версии
программы. Программистам приходится
изучать сотни различных API-функций.
Чтобы облегчить их труд, специалисты
Microsoft разработали библиотеку
MicrosoftFoundationClasses— MFC . Используя готовые
классы C++, можно гораздо быстрее и проще
решать многие задачи. Библиотека MFC
существенно облегчает программирование
в среде Windows. Классы библиотеки MFC
используются как для управления объектами
Windows, так и для решения определенных
общесистемных задач. По сути, в MFC
представлены практически все функции
WindowsAPI. В библиотеке имеются средства
обработки сообщений, диагностики ошибок
и другие средства, обычные для приложений
Windows. MFC обладает следующими преимуществами.
MicrosoftVisualC++ представляет собой
интегрированную среду разработки, в
которой вы можете легко создавать,
открывать, просматривать, редактировать,
сохранять, компилировать и отлаживать
все свои приложения, написанные на С
или C++. Преимуществом этой среды является
относительная простота и легкость в
изучении.

Запуск
Visual C++

Меню
File.

New

По
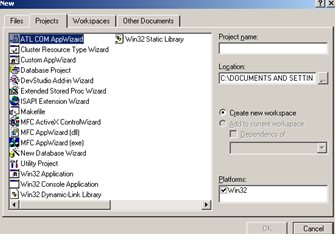
команде New…
открывается окно для выбора типа
создаваемого файла, проекта или рабочего
пространства. Именно с этой команды
обычно начинается работа над новым
приложением. VisualC++
автоматически присваивает название и
номер каждому создаваемому файлу (но
не проекту), если только вы не сделали
этого самостоятельно. Нумерация файлов
начинается с 1. Таким образом, первый
файл всегда будет иметь имя xxxl,
второй — ххх2 и т.д.

Open

В
отличие от команды New…,
предназначенной для создания нового
файла, команда Open…

открывает
диалоговое окно, с помощью которого вы
можете выбрать любой ранее

сохраненный
файл. Окно OpenFile
имеет стандартный вид для всех приложений
Windows.
В

случае
попытки открыть уже открытый файл будет
подан звуковой сигнал и показано

предупреждающее
сообщение.

Close

Команда
Close предназначена для закрытия ранее
открытого файла. Если у вас в настоящий
момент открыто несколько файлов, данная
команда закроет активное, т.е. текущее
окно. Если вы по ошибке попытаетесь
закрыть несохраненный файл, программа
предупредит о том, что вы рискуете
потерять информацию, и предложит
сохранить ее прямо сейчас.

Save

Команда
Saveсохраняет
содержимое текущего окна в соответствующем
файле. По строке заголовка окна можно
определить, соответствует ли активному
окну какой-нибудь файл на жестком диске.
Если вы открыли новое окно и еще не
сохраняли его, то в строке заголовка
будет показано стандартное имя вида
xxxl.
При попытке сохранить информацию из
окна, которому не соответствует ни один
файл, автоматически будет открыто
диалоговое окно

SaveAs

Команда
SaveAs…
позволяет сохранить содержимое окна в
файле под новым именем. Предположим, вы
только что закончили работу над проектом
и, имея вполне работоспособную программу,
хотите попытаться внести некоторые
изменения. В целях безопасности текущую
версию программы нужно сохранить. Для
этого вы выбираете команду SaveAs
и сохраняете проект под новым именем,
после чего можете спокойно экспериментировать
с дубликатом. Если эксперименты приведут
к повреждению программы, вы всегда
сможете вернуться к исходной версии.

SaveAll

Если
вам никогда ранее не приходилось
заниматься программированием на C/C++
в Windows95,98
или NT,
то поначалу вы будете ошеломлены обилием
файлов, вовлеченных в проект. Неудобство
команды Save
состоит в том, что она сохраняет содержимое
только одного, текущего окна. С помощью
команды SaveAll
можно сохранить все открытые на данный
момент файлы. Если содержимое каких-то
окон ранее не сохранялось в файлах, то
для них автоматически будет открываться
окно SaveAs,
где вы сможете вводить имена новых
файлов.

PageSetup

Данную
команду обычно используют перед выводом
файла на печать. В открывающемся при
этом диалоговом окне PageSetup
вы можете задать верхний и нижний
колонтитулы для каждой печатной страницы,
а также размеры, верхнего, нижнего,
правого и левого полей страницы.

Print

Чтобы
вывести на печать содержимое активного
окна, нужно выбрать из меню File
команду Print….
Откроется диалоговое окно Print,
в котором вы сможете установить требуемые
параметры печати. Прежде всего необходимо
решить, хотите вы вывести на печать все

содержимое
файла или только предварительно
выделенную часть. Если в активном окне
был выделен блок, то в окне Print
станет доступной опция Selection
группы PrintRange
(в противном случае переключатель
окажется недоступным). Если к компьютеру
подключено несколько устройств вывода,
вы можете выбрать нужный принтер и
произвести настройку параметров печати,
щелкнув на кнопке Setup.

RecentFiles
и RecentWorkspaces

Под
командой Print…
находятся списки недавно открывавшихся
файлов и проектов. Удобная особенность
таких списков состоит в том, что они
обновляются автоматически. Когда вы в
первый раз запускаете VisualC++,
оба списка пусты.

Exit

Команда
Exit
закрывает окно VisualC++.
Не беспокойтесь, если вы забыли сохранить
содержимое какого-нибудь файла. Программа
автоматически выдаст предупреждающие
сообщения для каждого несохраненного
файла.

Меню
Edit.

Undo

Команда
Undo
позволяет отменять последние выполненные
операции редактирования. Данная
возможность доступна также и через
соответствующую кнопку стандартной
панели инструментов (восьмая слева).

Redo

После
того как вы отменили последнее действие
с помощью команды Undo,
вы можете повторить операцию,
воспользовавшись командой Redo.
Этой команде соответствует девятая
слева кнопка стандартной панели
инструментов.

Cut

Команда
Cut
копирует выделенный блок текста из
активного окна в буфер обмена, после
чего удаляет этот блок из окна. Команду
Cut
обычно используют в сочетании с командой
Paste
для перемещения блока текста из одного
места в другое. На стандартной панели
инструментов ей соответствует пятая
кнопка слева.

Copy

Как
и команда Cut,
команда Сору копирует и помещает
выделенный блок текста в буфер обмена,
но этот блок сохраняется в активном
окне. Команду Сору обычно используют в
сочетании с командой Paste
при необходимости скопировать блок
текста из одного места в другое. Ей
соответствует шестая слева кнопка
стандартной панели инструментов.

Paste

Команда
Paste
предназначена для вставки информации
из буфера обмена в текущий документ (в
месторасположение текстового курсора).
На стандартной панели инструментов ей
соответствует седьмая слева кнопка.

Delete

Чтобы
удалить выделенный блок текста, не
копируя его в буфер обмена, можно
воспользоваться командой Delete.
Хотя удаленный текст и не будет скопирован
в буфер обмена, вы все равно сможете
восстановить его, если сразу после
удаления выберете в меню Edit
команду Undo.

SelectAll

Команда
SelectAll
используется для выделения всего
содержимого активного окна с целью
последующего вырезания, копирования
или удаления.

Find

Модуль
поиска, запускаемый командой Find…,
работает примерно так же, как и аналогичное
средство поиска в большинстве текстовых
редакторов. Поскольку языки C/C++
чувствительны к регистру символов,
опции диалогового окна Findпозволят
вам организовать поиск как с учетом,
так и без учета регистра, а также поиск
слова целиком. Можно задать и направление
поиска — вверх или вниз от текущего
положения курсора.

FindinFiles

При
выборе команды Find
in
Files…
вы получаете в свое распоряжение все
средства команды Find…
и возможность проводить поиск ключевых
слов сразу в нескольких файлах. Вы можете
спросить: «С какой стати я стану искать
что-нибудь сразу в нескольких файлах?»
Чтобы ответить на этот вопрос, вспомним,
что проект, написанный на C/C++,
состоит из множества взаимосвязанных
файлов. Предположим, в процессе
программирования вы поймете, что какую-то
часто используемую в приложении
конструкцию лучше заменить более
компактной. В таком случае, выполнив
команду Find
in
Files…,
вы будете уверены, что произвели замену
во всех файлах проекта. Если над каким-то
большим проектом работает группа людей,
то с помощью команды FindinFiles… вы сможете
отобрать файлы, автором которых является
определенный сотрудник. Кроме того,
помните, что возможности команды
FindinFiles… не ограничены одной папкой или
даже одним диском. С помощью этой команды
вы можете вести поиск в локальной сети,
в интранет и даже в Internet, отыскивая
заданные имена, строки, ключевые слова,
методы и многое другое.

Replace

При выборе
команды Replace..