Физика 7 класс что такое полезная работа

Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.

Что такое работа в физике – определение и формула

Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию. 

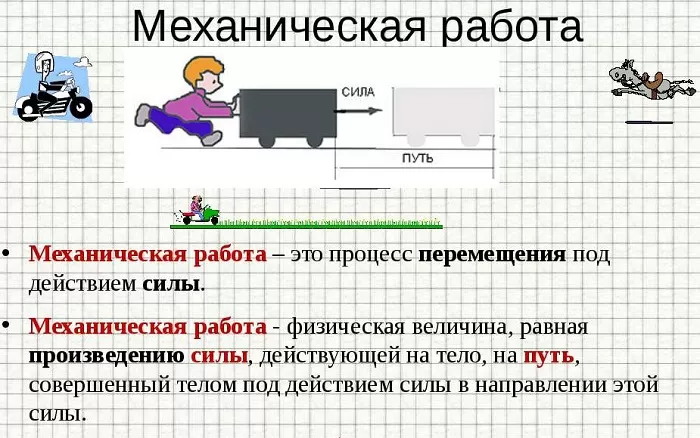
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:

A = F * S

В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:

A = F * S * cosA

В чем измеряется работа

Физические единицы, в которых выражается механическая работа, – Джоули. 

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах. 

Работа силы трения

При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной. 

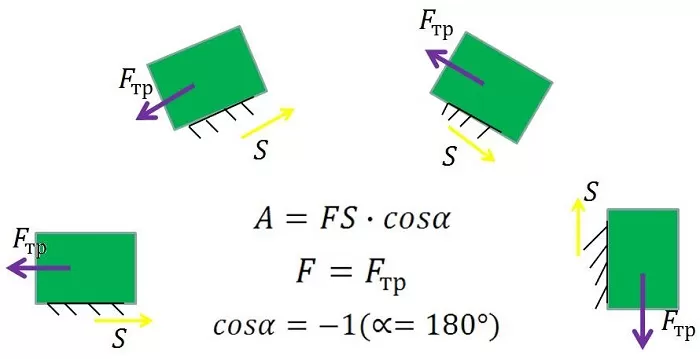
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.

Положительная и отрицательная работа

Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости. 

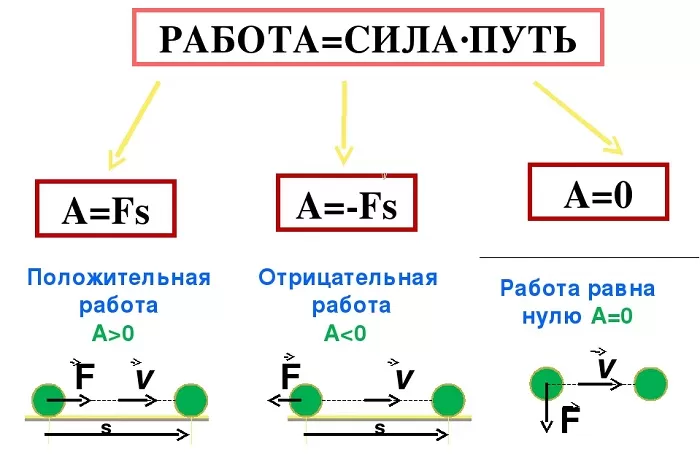
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей. 

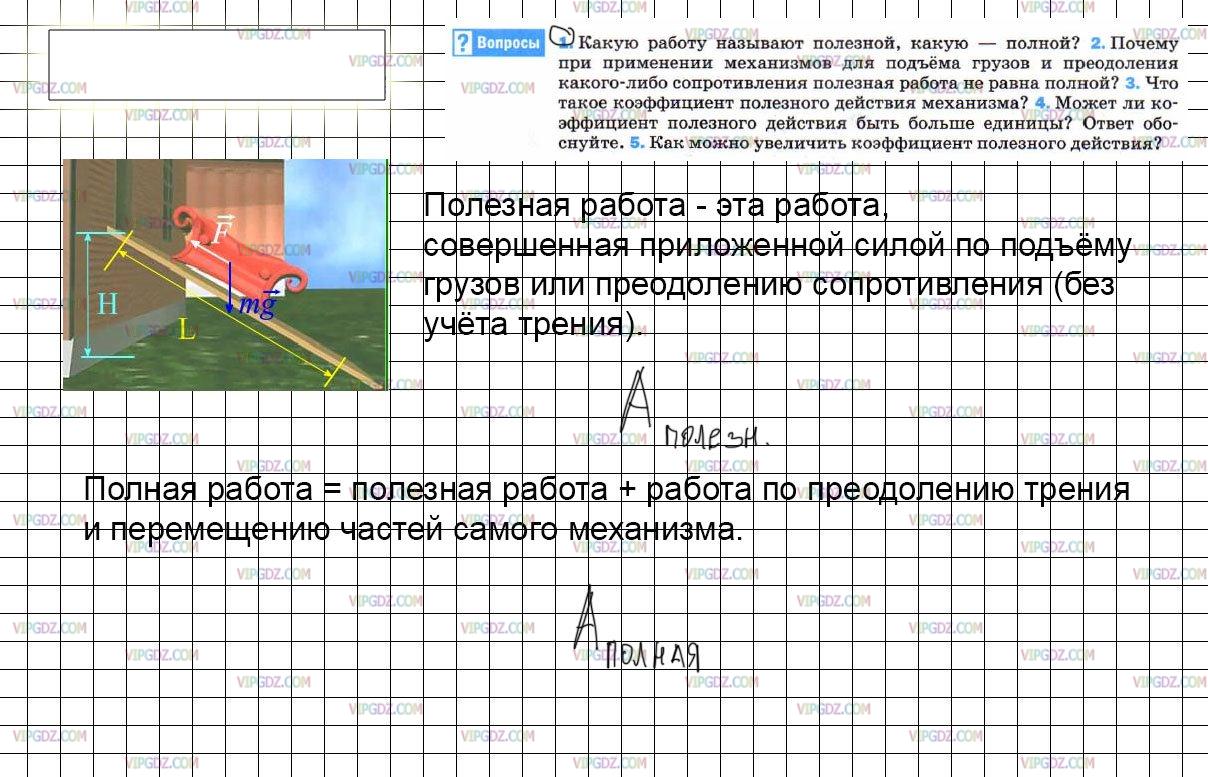
Полезная или затраченная работа

У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле. 

Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:

КПД = А полезная / А затраченная,

и выражается в процентах. КПД всегда меньше 100.

Мощность

Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:

Р = A / t

В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.

Однако при равномерном движении можно использовать и другую формулу:

Р = F * v

Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.

Примеры решения задач

Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1

Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.

Решение:

Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.

При помощи простой математики найдем числовой ответ:

A = 50 м * 10 кг * 10 Н/кг;

A = 5000 Дж.

Ответ: 5000 Дж.

Впрочем, не всегда речь идет о силе тяжести.

Задача 2

Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.

Решение:

Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.

Далее при помощи элементарных вычислений рассчитаем ответ:

A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.

Ответ: 0,4 Дж.

Но во всех задачах по данной теме траектория движения тела прямая.

Задача 3

Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.

Решение:

В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.

Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.

Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).

В таком случае:

F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.

Ответ: 5308 Н.

В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.

Задача 4

Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.

Решение:

На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы. 

Запишем условие в более наглядном виде.

Дано:

m = 2500 кг;

F = 10000 H;

t = 10 с;

КПД = 30%;

угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);

V – ?

Выведение формулы:

Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).

A1 = mg;

A2 = P * t / КПД.

То есть mg = P * t / КПД.

Шаг 2. P = F * V * cosA.

Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.

V = (m * g * КПД) / (F * t * cosA).

Числовое решение:

V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);

V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);

V = 7500 / 50000;

V = 0,15 м/с.

Ответ: 0,15 м/с.

Здравствуйте, дорогие друзья! Сегодня мы рассмотрим основные понятия физики и формулы, которые входят в программу учебника Физика 7 класс. Мы пройдем вкратце весь путь познания в области физики от таких базовых понятий, как объем и масса, до коэффициента полезного действия.

…

Количественные характеристики тела

Основные понятия физики – суть всех понятий, которые прямо или косвенно описывают природу явлений. Из количественных характеристик тела можно отметить его объем и массу. Приведем определение.

Объем представляет собой показатель того, сколько место занимает тело в пространстве. Уточним, что, если, к примеру, полая сфера и шар одинакового радиуса находятся в пространстве, то это не означает, что обе фигуры занимают в пространстве одинаковое количество места. Поясним это подробнее.

Полая сфера только на первый взгляд занимает столько же места, сколько шар, на деле их объемы различны – внутри сферы пустота, поэтому, рассчитывая объем, необходимо понимать, что объем воздуха внутри не входит в общую формулу.

Важно! Объем – величина, которая характеризует исключительно место, занимаемое телом. Объем не отражает суть влияние тела на само пространство и на другие тела. Тела одинаковой формы и размеров из совершенно различных материалов будут иметь одинаковые объемы. Формула объема также будет одинакова, как и его численное значение.

Для того чтобы характеризовать понятие объема, вспомним о том, каким образом мы измеряли размеры фигур на плоскости. Для этого мы пользовались понятием площадь. У плоских фигур не может быть объема, у объемных фигур может быть площадь, она называется площадью поверхности. Роль объема в физике очень велика, так как она отражает суть его размеров.

Приведем формулы некоторых фигур:

Формула объема параллелепипеда:

V = abc,

где abc – стороны.

Пирамиды:

,

где S – основание, Н – высота.

Конуса:

,

где R – радиус основания, Н – высота.

Цилиндра:

?=?,

где R – радиус основания, Н – высота.

Говоря о массе, необходимо помнить, что эта физическая величина, в отличие от объема, как раз отражает влияние тела на окружающие тела. Масса представляет собой меру инерции тела, это физическая величина, которая определяет его гравитационные характеристики.

Не следует путать вес с массой, поскольку вес – это сила, и она зависит от гравитационных условий, в котором тело «взвешивается».

Путь, время, скорость, ускорение

При движении тела оно проходит множество точек. Совокупность этих точек называется траекторией. Вектор между началом движения и концом называется перемещением. Если тело движется равномерно и прямолинейно, то перемещение, путь и расстояния равны.

При движении с постоянной скоростью тело проходит за равные промежутки времени равные отрезки пути. Его путь можно отметить формулой:

S = vt, где:

v – скорость тела, t – время его пути. Понятие скорости в физике является одним из самых базовых, поскольку отражает общую тенденцию движущегося тела.

Если в течение времени t1 тело прошло расстояние S1, затем, изменив свою скорость, прошло расстояние S2 за время t2, то есть смысл говорить о таком понятии, как средняя скорость.

Явление средней скорости в общем понимании можно рассматривать как среднее арифметическое двух его скоростей:

.

Если тело обе части пути проходило одно и то же расстояние S, то формула времени принимает вид:

.

Запишем время как отношение расстояния к скорости:

.

Тогда из этого соотношения можно получить выражение для средней скорости:

.

Если тело движется не с постоянной скоростью, но в течение одинаковых промежутков времени, его скорость одинаково меняется, то есть смысл говорить о равноускоренном движении (либо равнозамедленном, если скорость снижается, т.е. тело тормозит).

Важно! Именно равноускоренно двигаются все падающие тела. Ускорение соответствует ускорению свободного падения.

Введем понятие ускорения. Если тело двигалось со скоростью v0, спустя время t оно начало двигаться со скоростью v, то ускорением называется величина, равная:

В математике подобное отношение также называют производной скорости по времени. Зависимость скорости от каждого момента времени легко получить, отделив из формулы ускорения скорость:

.

Изобразим график зависимости скорости от времени:

Очевидно, что графиком является прямая, причем тангенсом угла наклона этой прямой будет ускорение.

Площадь трапеции под графиком – расстояние, которое прошло тело. Вычислить эту площадь довольно просто, нам известно, что площадь трапеции является полусуммой ее оснований, умноженной на высоту. Одно основание трапеции равно v0 (как раз место, где прямая пересекает координату скорости), второе основание равно v. Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:

.

Поскольку v = v0 + at, получаем:

.

Таким образом, при равноускоренном движении расстояние равно:

.

В случае, если речь идет о свободном падении, то вместо ускорения во все формулы должно быть поставлено ускорение свободного падения g=9,81 м/с2.

v = v0 + gt;

Если начальная скорость равна нулю, то:

.

Графиком зависимости пути от времени будет парабола (поскольку зависимость квадратичная):

Постараемся найти формулу времени для разных типов движений:

При равномерном движении:

.

При равноускоренном движении:

.

Вес, сила

Если кинематика занимается изучением того, как именно двигаются тела, то динамика подходит к понятию движения более глубоко – она изучают, почему они двигаются именно так. Здесь появляется понятие силы. Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.

Больше всего физического смысла данной величины отражается в главных четырех законах, которые носят названия «Три закона Ньютона» и «Закон всемирного тяготения«.

Первый закон Ньютона гласит, что если сумма всех сил равна нулю, то тело движется равномерно. Не стоит путать «сумма всех сил равна нулю» и «на тело не действуют никакие силы».

Знаменитый второй закон Ньютона устанавливает связь между динамической величиной силы, импульса и ускорения:

,

.

При постоянной массе:

F = ma.

В частности, если ускорение представляет собой ускорение свободного падения g, то сила превращается в вес:

Р = mg

Здесь мы на минуту остановимся и постараемся при помощи этих двух законов Ньютона усвоить несколько важных понятий.

Первый закон Ньютона гласит, что лежащее на поверхности тело хотя и находится в состоянии покоя (относительно земли), тем не менее, на него действуют две силы. Вес:

Р = mg

И нормаль (сила реакции опоры). Сумма этих сил равна нулю. Формула первого закона Ньютона может выглядеть таким образом:

Если

.

Вес является величиной относительной с точки зрения планет, на которых находятся тела. Например, часто можно услышать ошибочное высказывание: «масса тела на Луне меньше, чем на Земле». Это не так. Массы на всех планетах одинаковые, а вот вес разный, поскольку различается ускорение свободного падения. Именно поэтому космонавты на Луне с такой легкостью подпрыгивали – их вес на Луне был значительно ниже, чем на Земле, ведь Луна их притягивала к себе не так сильно, как Земля.

Третий закон Ньютона гласит, что сила действия равна силе противодействия. Иными словами, чем сильнее мы давим на тело, тем сильнее оно давит на нас. Этот закон отражает равенство силы тяжести и нормали.

.

,

где Fi — сила инерции.

Если есть система тел, то скорость центра масс системы равна:

.

Закон всемирного тяготения, который еще называют четвертым законом Ньютона, гласит:

,

где G – гравитационная постоянная, m1, m2  – массы притягивающихся тел.

Если в левой части этого равенства указать вес, то получаем формулу для ускорения свободного падения тел на любой планете:

.

Также, из закона всемирного тяготения выводится понятие первой космической скорости, т.е. скорости, при которой тело покидает гравитационное поле. Именно до этой скорости (на Земле она равна 7,9 км/с) разгоняют ракеты, которые необходимо вывести на орбиту.

Первая космическая скорость:

.

Вернемся к понятию веса.

Если тело находится в состоянии покоя, то вес равен:

Р = mg

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Р = m(g+a)

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Р = m(g-a)

Эта формула наглядно показывает, что в падающем лифте, где а = g, вес тела будет равен нулю, т.е. тело испытает невесомость.

Если тело движется по выпуклой траектории, то ускорение, действующее на него, – центробежное, а значит вес:

Р=m(g-v2/r).

Если тело движется по вогнутой траектории, то ускорение действующее на него — тоже центробежное и направлена от центра, а значит вес:

Р=m(g+v2/r).

Формула силы трения:

,

где  

— коэффициент трения, N — нормаль (реакция опоры).

Таким образом, мы познакомились уже с несколькими видами сил – вес (сила тяжести), сила трения, центробежная сила, сила всемирного тяготения (которая является по сути тем же весом, только в более общей форме).

Рассмотрим еще одну силу, которая имеет место в случае деформаций. Она называется силой упругости. Закон Гука для малых деформаций (сжатий или растяжений) гласит, что сила, действующая на тело, длину которого деформировали на х, равна:

Fупр = –kx.

Из этого закона вытекает ряд следствий, например модуль Юнга, который выступает коэффициентом пропорциональности в связи между нормальным напряжением и относительным изменением длины:

.

Энергия, работа, мощность, полезное действие

Для того чтобы описывать различные формы взаимодействия материи и ее движение, вводится физическая величина энергия. Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):

A = FS

Если тело движется со скоростью v, то тело обладает энергией, которая называется кинетической:

.

Если тело приподняли на высоту h, то оно обладает в точке подъеме потенциальной энергией:

E = mgh/.

Важно ! По сути, потенциальная энергия представляет собой работу силы тяжести. Если сила тяжести mg, а путь, пройденный телом, – высота h, на которую его подняли, то работа A = F

S = mgh.

При падении тела с высоты Н его потенциальная энергия превращается в кинетическую.

Закон сохранения энергии гласит, что в замкнутых системах энергия сохраняется. Таким образом, если тело подняли на высоту h и отпустили, то скорость, с которой оно будет приземляться, можно вычислить из закона сохранения:

.

Отсюда:

.

Остановимся подробнее на двух законах сохранения: законе сохранения энергии и импульса.

Импульс в замкнутых системах сохраняется, энергия в замкнутых системах сохраняется. В паре эти два закона могут разрешить бесконечное количество задач. Рассмотрим пример.

Задача на закон сохранения энергии и импульса

Задача. Идеально упругий шарик массой m движется со скоростью v и ударяется о покоящийся шарик массой M. Удар будет центральный, т.е. траектория шарика и ось между их центрами – одна и та же линия.

Какая будет скорость u шарика массой M и скорость v1 шарика массой m после удара?

Решение:

Первый шарик до столкновения обладал импульсом mv. Второй шарик находился в состоянии покоя, т.е. его импульс был равен M∙0 = 0.

Таким образом, в системе двух шариков суммарный импульс до столкновения был равен:

.

После столкновения импульс первого шарика стал равен mv1, а импульс второго шарика составил Mu. Тогда суммарный импульс системы двух шариков после удара равен:

Согласно закону сохранения импульса Р = Р1, а именно:

(1).

Теперь рассмотрим энергии. Кинетическая энергия первого шарика до удара составила 

. Кинетическая энергия второго шарика равна нулю. После удара первый шарик имеет кинетическую энергию . Второй шарик после удара обладает энергией:.

Согласно закону сохранения энергии:

.

Сократив двойки в знаменателях, получаем:

(2).

Получаем систему из двух выражений (1) и (2).

(*).

Из первого уравнения можем получить выражение для скорости первого шарика после удара:

(3).

Найдем квадрат этой скорости:

.

Найдем значение выражения:

.

Те?