Физика 7 класс полезная работа это

Термины по физике 7 класс
Физика. Наука, изучающая явления природы, свойства и строение материи.
Материя. Всё, что есть во Вселенной.
Молекула. Мельчайшая частица данного вещества.
Диффузия. Взаимное перемешивание молекул одного вещества с молекулами другого.
Механическое движение. Изменение положения тела относительно других тел с течением времени.
Путь. Длина траектории.
Траектория. Линия, по которой движется тело.
Равномерное движение. Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Скорость. Величина, равная отношению пути ко времени, за которое этот путь пройден.
Инерция. Явление сохранения скорости тела при отсутствии действия на него других тел.
Тормозной путь. Путь, который проходит автомобиль после выключения двигателя до полной остановки.
Плотность. Физическая величина, равная отношению массы тела к его объёму.
Сила. Мера механического воздействия на тело со стороны других тел.
Масса. Мера инертности.
Вес. Сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Равнодействующая сила. Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Сила трения. Сила, возникающая при движении одного тела по поверхности другого и направленная против движения.
Давление. Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
Атмосфера. Воздушная оболочка Земли.
Архимедова сила. Сила, выталкивающая тело из жидкости или газа.
Работа. Величина, равная произведению приложенной силы на пройденный путь.
Мощность. Величина, равная отношению работы ко времени, за которое она была совершена.
Рычаг. Твёрдое тело, которое может вращаться вокруг неподвижной опоры.
КПД. Отношение полезной работы к полной работе.
Потенциальная энергия. Энергия взаимодействия.
Кинетическая энергия. Энергия движения.
Определения и формулы
Определения и формулы по физике за 7 класс, структурированные в порядке изучения тем
Измерение физических величин
Определения и формулы по теме »
Измерение физических величин
Цена деления шкалы прибора
Для определения цены деления (ЦД) шкалы прибора необходимо:
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
Формула:
ЦД = (ВГ — НГ) / N
ЦД = (Б — А) / n
Механическое движение
Определения и формулы по теме «Механическое движение»
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).
Формула:
ʋ = S / t
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.
Формула:
S= ʋ*t
Время движения (t) — равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.
Формула
t = S / ʋ:
Средняя скорость (ʋср) — равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.
Формула:
ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
Сила тяжести, вес, масса, плотность
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)
Формула:
FТ = m*g
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).
Формула:
Р = m*g
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).
Формула:
т = Р / g
Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).
Формула:
ρ = m / V
Механический рычаг, момент силы
Момент силы (М) равен произведению силы (F) на сё плечо (l)
Формула:
М = F*l
Условие равновесия рычага — рычаг находится в равновесии, если плечи (l1, l2)действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.
Формула:
a) F1 / F2 = l1 / l2
б) F1*l1 = F2*l2
Давление, сила давления
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности
Формула:
p = F / S
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)
Формула:
F = р*S
Давление газов и жидкостей
Давление однородной жидкости (р) — на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).
Формула:
p = g ρ h
Закон Архимеда — на тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.
Формула:
FВ = ρ*g*Vт
Условие плавания тел — если архимедова сила (FВ) больше силы тяжести (FТ)тела, то тело всплывает.
Формула:
FВ > FТ
Закон гидравлической машины — силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.
Формула:
F1 / F2 = S1 / S2
Закон сообщающихся сосудов — однородная жидкость в сообщающихся сосудах находится на одном уровне (h)
Формула:
h = const
Работа, энергия, мощность
Механическая работа — Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.
Формула:
А = F*S
Коэффициент полезного действия механизма (КПД) — коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).
Формула:
ɳ = АП / АВ *100%
Потенциальная энергия (ЕП) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.
Формула:
ЕП = m*g*h
Кинетическая энергия (ЕК) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ2).
Формула:
ЕК = m*ʋ2 / 2
Сохранение и превращение механической энергии — Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.
Формула:
EП + EК = const
Мощность (N) — величина, показывающая скорость выполнения работы и равная:
а) отношению работы (А) ко времени (t), за которое она выполнена;
б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.
Формула:
N = A / t
N = F*ʋ
Формулы меры длины и веса и соотношения между единицами

12 самых востребованных формул по физике в 7 классе


Источник
| ««« [ ] »»» | ||
| § 05-б. Коэффициент полезного действия | ||
Допустим, мы отдыхаем на даче, и нам нужно принести из колодца воды. Мы опускаем в него ведро, зачерпываем воду и начинаем поднимать. Не забыли, какова наша цель? Правильно: набрать воды. Но взгляните: мы поднимаем не только воду, но и само ведро, а также тяжёлую цепь, на которой оно висит. Это символизирует двухцветная стрелка: вес поднимаемого нами груза складывается из веса воды и веса ведра и цепи.
Рассматривая ситуацию качественно, мы скажем: наряду с полезной работой по подъёму воды мы совершаем и другую работу – подъём ведра и цепи. Разумеется, без цепи и ведра мы не смогли бы набрать воды, однако, с точки зрения конечной цели, их вес «вредит» нам. Если бы этот вес был бы меньше, то и полная совершённая работа тоже была бы меньше (при той же полезной). Теперь перейдём к количественному изучению этих работ и введём физическую величину, называемую коэффициентом полезного действия. Задача. Яблоки, отобранные для переработки, грузчик высыпает из корзин в грузовик. Масса пустой корзины 2 кг, а яблок в ней – 18 кг. Чему равна доля полезной работы грузчика от его полной работы? Решение. Полной работой является перемещение яблок в корзинах. Эта работа складывается из подъёма яблок и подъёма корзин. Важно: поднятие яблок – полезная работа, а поднятие корзин – «бесполезная», потому что цель работы грузчика – переместить только яблоки.
| ||
Введём обозначения: Fя – сила, с которой руки поднимают вверх только яблоки, а Fк – сила, с которой руки поднимают вверх только корзину. Каждая из этих сил равна соответствующей силе тяжести: F=mg. Пользуясь формулой A = ±( F||· l ) , «распишем» работы этих двух сил: Aполезн = +Fя · lя = mяg · h и Aбесполезн = +Fк · lк = mкg · h Полная работа складывается из двух работ, то есть равна их сумме: Aполн = Aполезн + Aбесполезн = mяg h + mкg h = ( mя + mк ) · g h В задаче нас просят вычислить долю полезной работы грузчика от его полной работы. Сделаем это, поделив полезную работу на полную:
В физике такие доли принято выражать в процентах и обозначать греческой буквой «η» (читается: «эта»). В итоге получим: η = 0,9 или η = 0,9 ·100% = 90% , что то же самое. Это число показывает, что из 100% полной работы грузчика доля его полезной работы составляет 90%. Задача решена. Физическая величина, равная отношению полезной работы к полной совершённой работе, в физике имеет собственное название – КПД – коэффициент полезного действия:
После вычисления КПД по этой формуле его принято умножать на 100%. И наоборот: для подстановки КПД в эту формулу его значение нужно перевести из процентов в десятичную дробь, поделив на 100%.
| ||||||||||||||||||||||||
Источник
ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 7 класс
- Физика
- Пёрышкин
- Вопрос 1, Параграф 65

Назад к содержанию
Условие
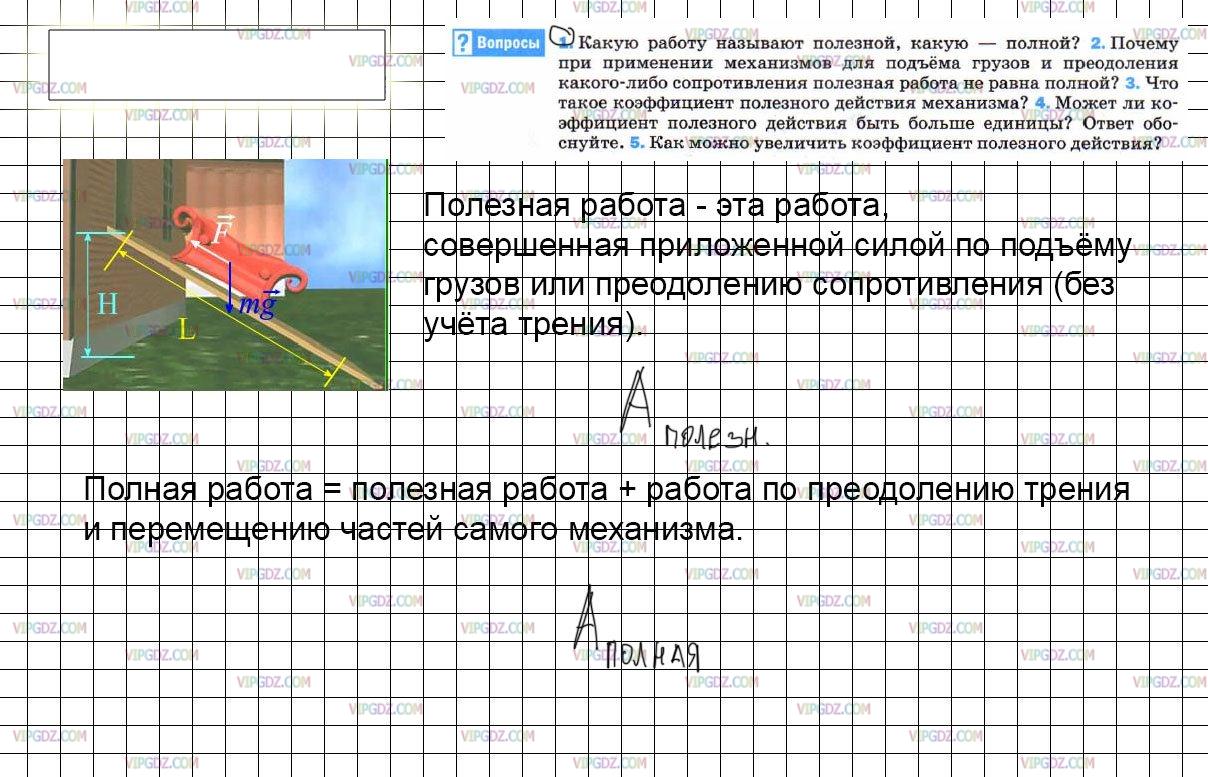
Какую работу называют полезной, какую — полной?
Решение 1

Решение 2

Решение 3
Другие задачи из этого учебника
- 1
- 2
- 3
- 4
- 5
Поиск в решебнике
Популярные решебники
 ГДЗ по Физике за 7 класс: Пёрышкин А.В.
ГДЗ по Физике за 7 класс: Пёрышкин А.В.
Издатель: А. В. Перышкин — 2013г.
 ГДЗ по Физике за 7-9 класс: Пёрышкин А.В. (сборник задач)
ГДЗ по Физике за 7-9 класс: Пёрышкин А.В. (сборник задач)
Издатель: А.В. Пёрышкин, 2013г.
Источник
Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
Используемые обозначения[править | править код]
Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).
Определение[править | править код]
Работа силы, приложенной к материальной точке[править | править код]
Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:
Здесь точкой обозначено скалярное произведение, — вектор перемещения; подразумевается, что действующая сила постоянна в течение времени, за которое вычисляется работа.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[2]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).
Если существует зависимость силы от координат[3], интеграл определяется[4] следующим образом:
,
где и — радиус-векторы начального и конечного положения тела соответственно.
- Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.
Работа сил, приложенных к системе материальных точек[править | править код]
Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).
Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия[править | править код]
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если — полная работа, совершённая над частицей, определяемая как сумма работ, совершённых приложенными к частице силами, то она выражается как:
где называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как[5]:
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия[править | править код]
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая, что
Если все силы, действующие на частицу, консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:
.
Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,
,
является постоянной во времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике[править | править код]
В термодинамике работа, совершённая газом при расширении[6], рассчитывается как интеграл давления по объёму:
Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.
Работа силы в теоретической механике[править | править код]
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, , и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).
Величина , называется элементарной работой силы на участке и принимается за приближённое значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .
В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .
Таким образом, если обозначить эту работу буквой , то, в силу данного определения,
,
следовательно,
(1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим
Размерность и единицы[править | править код]
Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг
1 Дж = 1 кг·м²/с² = 1 Н·м
1 эрг = 1 г·см²/с² = 1 дин·см
1 эрг = 10−7Дж
См. также[править | править код]
- Закон сохранения энергии
- Теорема о кинетической энергии системы
- Механические приложения криволинейных интегралов
Примечания[править | править код]
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях суммируется, что и даёт в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература[править | править код]
- История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
- Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
- Льоцци М. История физики. М.: Мир, 1970.
- Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
- Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.
Источник


