Как найти полезную работу идеального газа
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
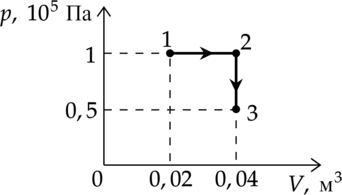
Работа газа – площадь под графиком: [A=p_1cdot(V_2-V_1)=10^5text{ Па}cdot(0,04text{ м$^3$}-0,02text{ м$^3$})=2000text{ Дж}=2text{ кДж}]
Ответ: 2
Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=300text{ Дж}-100text{ Дж}=200 text{ Дж}]
Ответ: 200
Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=100text{ Дж}-(-100text{ Дж})=200 text{ Дж}]
Ответ: 200
На pV-диаграмме изображены циклические процессы, совершаемые идеальным газом в количестве 1 моль. Определите отношение работы газа в циклическом процессе ВСDВ к работе газа в циклическом процессе АВDFА.
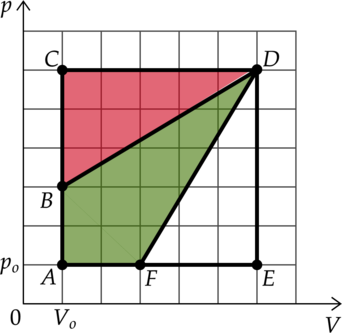[frac{A_{BCDB}}{A_{ABDFA}}=frac{0,5cdot3cdot5}{5cdot5-2cdot0,5cdot3cdot5}=0,75]
Ответ: 0,75
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразите в кДж.
Первое начало термодинамики: [Q=Delta U+A_{text{г}}] [A_{text{г}}=Q-Delta U]
Подставим исходные значения: [A_{text{г}}=Q-Delta U=-10text{ кДж}-30text{ кДж}=-40 text{ кДж}] [A_{text{вн.с.}}=-A_{text{г}}=40 text{ кДж}]
Ответ: 40
В цилиндр с подвижным поршнем накачали (nu = 2) моля идеального одноатомного газа при температуре (t_1 = 50) (^{circ}C). Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры (t_2 = 20) (^{circ}C). Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна. Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ дайте в кДж округлите до целых.
В первом процессе газ расширяется при постоянном давлении. От объема 0 до (V_1) [A_{1-2}=p(V_1-0)=pV_1=nu RT_1]
Без теплообмена с окружающей средой означает, что процесс – адиабатический [Q=Delta U+A_{2-3}=0] [A_{2-3}=-Delta U_{2-3}]
Подставим исходные значения: [A=A_{1-2}+A_{2-3}=nu RT_1+frac{3}{2}nu R(T_1-T_2)=] [=2text{ моль}cdot8,3text{ Дж/моль·К}cdot323text{ K}+frac{3}{2}cdot2text{ моль}cdot8,3text{ Дж/моль·К}cdot30{ K}approx 6000text{ Дж}approx 6 text{ кДж}]
Ответ: 6
С массой (m = 80) г идеального газа, молярная масса которого (M = 28) г/моль, совершается циклический процесс, изображенный на рисунке. Какую работу (A) совершает такой двигатель за один цикл, если (T_1 = 300) К, (T_2 = 1000) К, а при нагревании на участке 4 – 1 давление газа увеличивается в 2 раза? Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ округлите до целых.
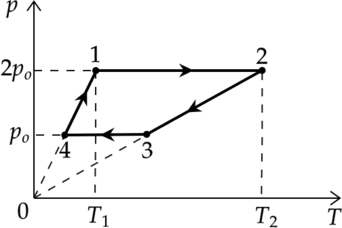
1-2 и 3-4 – изобарные процессы
2-3 и 4-1 – изохорные процессы
Перерисуем график в координатах (pV)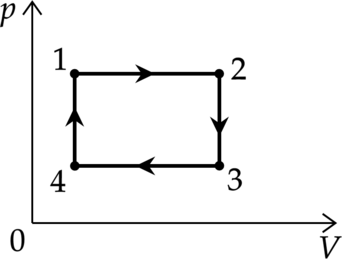 
Так как 2-3 и 4-1 – изохорные процессы, то (Tsim p). Давление увеличивается в 2 раза, то температура увеличивается в 2 раза. Следовательно: [T_4=frac{T_1}{2}=150 text{ К}] [T_3=frac{T_2}{2}=500 text{ К}]
Работа газа цикл – площадь внутри графика в координатах (pV) [A=(p_1-p_4)cdot(V_2-V_1)=(2p_4-p_4)cdot(V_2-V_1)=p_4cdot(V_2-V_1)=p_4V_2-p_4V_1]
Подставим исходные значения,переведя все единицы в систему СИ: [A=p_4V_2-p_4V_1=nu RT_3-nu RT_4=nu R(T_3-T_4)=frac{m}{M}R(T_3-T_4)=] [=frac{0,08text{ кг}}{0,028text{ кг/моль}}cdot8,31text{ Дж/(моль$cdot$ К)}cdot(500 text{ К} — 150 text{ К})= 8310 text{ Дж}]
Ответ: 8310
Источник
Имея уравнение состояния (1.7) идеального газа, мы найдем совершаемую им работу при некоторых типичных процессах. Заодно определим количество теплоты, получаемое от внешнего источника.
1. Изохорный процесс. При изохорном нагревании или охлаждении (соответственно, прямые 1–2 и 1–3 на рис. 2.7) работа просто равна нулю, поскольку объем не меняется.
Рис. 2.7. определению работы в изохорном процессе
Получаемое количество теплоты (обозначим Q12при V = const через Q12V) полностью идет на изменение внутренней энергии газа (см. (1.19))
Ту же самую величину можно выразить через изменение температуры газа
(2.7) |
2. Изобарный процесс. Поскольку в этом процессе р = const, то давление можно вынести из-под знака интеграла в (2.3). Тогда получаем (рис. 2.8)
(2.8) |
Рис. 2.8. Работа в изобарном процессе
Изменение внутренней энергии газа следует из (1.17) – (1.19) 1.17
1.18
1.19
:
(2.9) |
Складывая (2.8) и (2.9), находим количество теплоты, переданное газу в этом процессе:
(2.10) |
Пример 1. Пусть система получила при постоянном давлении определенное количество теплоты Q. Найдем, какая часть расходуется на совершение работы А, а какая — на увеличение внутренней энергии газа. Определим также, как зависит ответ от вида используемого газа.
Из формул (2.8) и (2.9) сразу следует, что
Чем больше g, тем большая часть тепла переходит в работу: для одноатомных газов
для двухатомных (без учета колебаний ядер, при двух вращательных степенях свободы)
и для многоатомных газов (без учета колебаний ядер, при трех вращательных степенях свободы)
Заметим, что мы излагаем достаточно общий подход, который применим не только к идеальным газам. Для иных систем может измениться уравнение состояния, как следствие изменятся выражения для совершенной работы, но принципы их вывода остаются одними и теми же. Приведем пример. Пусть для некоторой системы давление, температура и объем связаны соотношением
(2.11) |
Найдем выражение для работы такой системы при изменении ее температуры от Т1до Т2при постоянном давлении. Поскольку давление постоянно, имеем для работы в изобарном процессе стандартное выражение
Используя уравнение состояния (2.11), находим отсюда
3. Изотермический процесс расширения (или сжатия) газа может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной разности температур. Для этого теплоемкость внешней среды должна быть достаточно велика, и процесс расширения (или сжатия) должен происходить достаточно медленно. Диаграмма изотермического расширения представлена на рис. 2.9.
Рис. 2.9. Работа при изотермическом расширении системы
Используя уравнение состояния и выражение (2.2) для элементарной работы, находим
(2.12) |
Далее используем общее выражение (2.3) для работы при конечном изменении объема
(2.13) |
Поскольку объем обратно пропорционален давлению, тот же результат можно представить в виде
(2.14) |
Так как внутренняя энергия идеального газа не меняется при изотермическом процессе, в работу преобразовалась вся теплота, полученная от источника:
Пример 2. Расширяясь, водород совершил работу 6 кДж. Найдем количество теплоты, подведенное к газу, если процесс протекал: а) изобарно; б) изотермически.
Рассмотрим сначала изобарное расширение. Из формул (2.8) и (2.10) следует связь количества теплоты и совершенной работы:
Мы использовали значение g = 7/5 для двухатомного газа. Для изотермического расширения, как мы видели, полученное количество теплоты просто равно произведенной работе:
Видео 2.1. Работа нагретого газа над вертушкой.
Дополнительная информация
https://kvant.mirror1.mccme.ru/ — Журнал Квант, 2004, № 3, стр. 32–33, А. Леонович «А так ли хорошо знакома вам теплопередача?», — попробуйте ответить на оригинальные вопросы, связанные с теплообменом.
Источник
ВНУТРЕННЯЯ ЭНЕРГИЯ
Под внутренней энергией термодинамической системы понимают кинетическую энергию теплового движения ее молекул и потенциальную энергию их взаимодействия. Она зависит от параметров состояния V,T . Внутренняя энергия идеального одноатомного газа прямо пропорциональна его абсолютной температуре:
Для газов, состоящих из более сложных молекул, также U ~ Т , но коэффициент пропорциональности другой. Это объясняется тем, что такие молекулы не только движутся поступательно, но и вращаются.
РАБОТА В ТЕРМОДИНАМИКЕ
Если газ расширяется при постоянном давлении р, то сила, действующая со стороны газа на поршень: F = рS, гдеS — площадь поршня.
При подъеме поршня на высоту газ совершает работу
где ΔV — изменение объема газа.
При медленном сжимании газа работа, совершаемая внешними телами над газом, будет отличаться только знаком:
Работа, совершаемая термодинамической системой при постоянном давлении, равна
КОЛИЧЕСТВО ТЕПЛОТЫ
Процесс передачи энергии от одного тела к другому без совершения работы называют теплообменом.
Количество теплоты — это энергия, переданная телу в результате теплообмена.
Теплоемкость С — количество теплоты, необходимое для нагревания тела массой m на 1 К. Удельная теплоемкость с — это количество теплоты, которое получает или отдает 1 кг вещества при изменении его температуры на 1 К: c=C/m
Для изменения температуры вещества массой m от Т1 до Т2 ему необходимо сообщить количество теплоты
Коэффициент с в этой формуле называют удельной теплоемкостью: [с]=1 Дж/(кг*К).
При нагревании тела Q > 0, при охлаждении Q < 0.
Для того, чтобы жидкость массы m полностью превратить в пар, ей необходимо передать количество теплоты
Q=rm
где r — удельная теплота парообразования: [r] = 1 Дж/кг .
Удельная теплота парообразования — это количество теплоты, которое необходимо для превращения 1 кг жидкости в пар при постоянной температуре.
Конденсация — процесс, обратный испарению.
Для того, чтобы расплавить полностью тело массой m , ему необходимо сообщить количество теплоты
Q= λm
где — удельная теплота плавления: {λ} = 1 Дж/кг .
Удельная теплота плавления — это количество теплоты, которое необходимо для плавления 1 кг кристаллического вещества при температуре плавления.
Кристаллизация — процесс, обратный плавлению.
Для замкнутой системы, состоящей из N тел, можно записать уравнение теплового баланса:
Q1+…+Qn=0
где Q1, … , QN — количества теплоты, полученные или отданные телами.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Закон сохранения энергии
Энергия не возникает из ничего и не исчезает, она только переходит из одной формы в другую. Закон сохранения энергии, распространенный на тепловые явления, называется первым законом термодинамики.
Первый закон термодинамики
Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Этот закон можно сформулировать иначе:
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
В первой формулировке А — работа, совершаемая над системой (над газом), во второй А’ — это работа, совершаемая системой (газом).
Вечный двигатель первого рода — устройство, способное совершать неограниченное количество работы без подведения энергии извне.
Из первого закона термодинамики следует невозможность создания вечного двигателя первого рода. Если к системе не поступает теплота, то
Иными словами, работа совершается системой за счет уменьшения ее внутренней энергии. После того, как запас энергии будет исчерпан, двигатель перестанет работать.
Процесс, протекающий в теплоизолированной системе, называют адиабатным.
Абсолютно исключить теплопередачу невозможно, но иногда реальные процессы близки к адиабатным. Они протекают за очень малый промежуток времени, в течение которого не происходит существенного теплообмена между системой и внешними телами.
ТЕПЛОВЫЕ ДВИГАТЕЛИ
Тепловые двигатели — устройства, превращающие внутреннюю энергию топлива в механическую энергию.
Любой тепловой двигатель состоит из трех основных частей.
Рабочее тело — газ, совершающий работу А’ при расширении.
Нагреватель — устройство, от которого рабочее тело получает количество теплоты Q 1
Холодильник — устройство, которому рабочее тело передает количество теплоты Q2
Коэффициентом полезного действия (КПД) теплового двигателя называют отношение работы,совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
Так как Q2 < Q1, то всегда < 1.
Идеальная тепловая машина Карно — модель теплового двигателя, в котором рабочим телом
является идеальный газ. КПД машины Карно
где Т1 — температура нагревателя, T2 — температура холодильника.
Реальная тепловая машина не может иметь КПД, превышающий КПД идеальной тепловой машины.
Пример. Объем кислорода массой 160 г, температура которого 27°С, при изобарном нагревании увеличился вдвое. Найдите работу газа при расширении, количество теплоты, которое пошло на нагревание кислорода, изменение внутренней энергии.
Величина работы, совершаемой газом при изобарном процессе, когда V = V2 — V1 = V1, определяется выражением
С учетом уравнения состояния
можно записать
Изменение внутренней энергии двухатомного газа, с учетом уравнения состояния, будет выглядеть:
Учитывая, что А| = pV1, получим:
Количество теплоты, переданное газу, согласно первому закону термодинамики, идет на изменение его внутренней энергии и совершение газом работы:
Ответ: работа газа равна 12,5 кДж, количество теплоты, которое пошло на его нагревание, равно 43,8 кДж, изменение внутренней энергии — 31,3 кДж .
Источник
Историческая
справка.
1) М.В.
Ломоносов, проведя стройные рассуждения и простые опыты, пришел к выводу, что «причина
теплоты состоит во внутреннем движении частиц связанной материи… Весьма
известно, что тепло возбуждается движением: руки от взаимного трения
согреваются, дерево загорается, искры вылетают при ударе кремнием о сталь,
железо накаливается при ковании его частиц сильными ударами»
2) Б. Румфорд,
работая на заводе по изготовлению пушек, заметил, что при сверлении пушечного
ствола он сильно нагревается. Например, он помещал металлический цилиндр массой
около 50 кг в ящик с водой и, сверля цилиндр сверлом, доводил воду в ящике до
кипения за 2.5часа.
3) Дэви в 1799
году осуществил интересный опыт. Два куска льда при трении одного о другой
начали таять и превращаться в воду.
4) Корабельный
врач Роберт Майер в 1840 году во время плавания на остров Яву заметил, что
после шторма вода в море всегда теплее, чем до него.
Вычисление работы.
В механике
работа определяется как произведение модулей силы и перемещения: A=FS. При
рассмотрении термодинамических процессов механическое перемещение макротел в
целом не рассматривается. Понятие работы здесь связывается с изменением объема
тела, т.е. перемещением частей макротела друг относительно друга. Процесс этот
приводит к изменению расстояния между частицами, а также часто к изменению
скоростей их движения, следовательно, к изменению внутренней энергии тела.
Пусть в
цилиндре с подвижным поршнем находится газ при температуре T1
(рис.). Будем медленно нагревать газ до температуры T2. Газ
будет изобарно расширяться, и поршень переместится из положения 1 в
положение 2 на расстояние Δl. Сила давления газа при этом
совершит работу над внешними телами. Так как p = const, то и сила
давления F = pS тоже постоянная. Поэтому работу этой силы можно
рассчитать по формуле A=FΔl=pSΔl=pΔV, A= pΔV
где ΔV
— изменение объема газа. Если объем газа не изменяется (изохорный процесс), то
работа газа равна нулю.
Почему при
сжатии или расширении меняется внутренняя энергия тела? Почему при сжатии газ
нагревается, а при расширении охлаждается?
Причиной
изменения температуры газа при сжатии и расширении является следующее: при
упругих соударениях молекул с движущимся поршнем их кинетическая энергия
изменяется.
- Если газ сжимается, то при
столкновении движущийся навстречу поршень передаёт молекулам часть своей
механической энергии, в результате чего газ нагревается;
- Если газ расширяется, то после
столкновения с удаляющимся поршнем скорости молекул уменьшаются. в
результате чего газ охлаждается.
При сжатии и
расширении меняется и средняя потенциальная энергия взаимодействия молекул, так
как при этом меняется среднее расстояние между молекулами.
Работа
внешних сил, действующих на газ
- При сжатии газа, когда ΔV = V2 – V1 < 0 , A>0,
направления силы и перемещения совпадают; - При расширении, когда ΔV = V2 – V1 > 0 , A<0, направления
силы и перемещения противоположны.
Запишем
уравнение Клапейрона-Менделеева для двух состояний газа:
pV1=m/M*RT1; pV2=m/M*RT2⇒
p(V2−V1)= m/M*R(T2−T1).
Следовательно,
при изобарном процессе
A=m/M*RΔT.
Если m
= М (1 моль идеального газа), то при ΔΤ = 1 К получим R = A.
Отсюда вытекает физический смысл
универсальной газовой постоянной:
она численно равна работе, совершаемой 1 моль идеального газа при его изобарном
нагревании на 1 К.
Геометрическое истолкование работы:
На графике p = f(V) при изобарном процессе работа
равна площади заштрихованного на рисунке а) прямоугольника.
Если процесс
не изобарный (рис. б), то кривую p = f(V) можно
представить как ломаную, состоящую из большого количества изохор и изобар.
Работа на изохорных участках равна нулю, а суммарная работа на всех изобарных
участках будет равна площади заштрихованной фигуры. При изотермическом процессе
(Т = const) работа равна площади заштрихованной фигуры, изображенной на
рисунке в.
Источник