Как найти среднюю полезную мощность формула
Определение и формула полезной мощности
Определение
Мощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют
для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($Delta A$) к промежутку времени за которое она выполнена ($Delta t$) называют средней мощностью ($leftlangle Prightrangle $) за это время:
[leftlangle Prightrangle =frac{Delta A}{Delta t}left(1right).]
Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $Delta tto 0$:
[P={mathop{lim }_{Delta tto 0} frac{Delta A}{Delta t} }=A'(t)left(2right).]
Приняв во внимание, что:
[Delta A=overline{F}cdot Delta overline{r }left(3right),]
где $Delta overline{r }$ — перемещение тела под действием силы $overline{F}$, в выражении (2) имеем:
[P={mathop{lim }_{Delta tto 0} left(frac{overline{F}cdot Delta overline{r }}{Delta t}right) }=overline{F}{mathop{lim }_{Delta tto 0} left(frac{Delta overline{r }}{Delta t}right)= }overline{F}cdot overline{v}left(4right),]
где $ overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
[eta =frac{P_p}{P}left(5right),]
где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
[P=?I left(7right),]
где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.
Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
[P=?I=UI+I^2r=P_p+P_0left(8right),]
где $P_p=UI=I^2R=frac{U^2}{R}(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:
[eta =frac{P_p}{P_p+P_0}left(9right).]
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1
Задание. Коэффициент полезного действия электрического двигателя равен $eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двигатель идет ток силой $I=$10 А?
Решение. За основу решения задачи примем формулу:
[P_p=eta P left(1.1right).]
Полную мощность найдем, используя выражение:
[P=IUleft(1.2right).]
Подставляя правую часть выражения (1.2) в (1.1) находим, что:
[P_p=eta IU.]
Вычислим искомую мощность:
[P_p=eta IU=0,42cdot 110cdot 10=462 left(Втright).]
Ответ. $P_p=462$ Вт
Пример 2
Задание. Какова максимальная полезная мощность источника тока, если ток короткого замыкания его
равен $I_k$? При соединении с источником тока сопротивления $R$, по цепи (рис.1) идет ток силой $I$.

Решение. По закону Ома для цепи с источником тока мы имеем:
[I=frac{varepsilon}{R+r}left(2.1right),]
где $varepsilon$ — ЭДС источника тока; $r$ — его внутреннее сопротивление.
При коротком замыкании считаем, что сопротивление внешней нагрузки равно нулю ($R=0$), тогда сила тока короткого замыкания равна:
[I_k=frac{varepsilon}{r} left(2.2right).]
Максимальная полезная мощность в цепи рис.1 электрический ток даст, при условии:
[R=r left(2.3right).]
Тогда сила тока в цепи равна:
[I’=frac{varepsilon}{r+r}=frac{varepsilon}{2r}left(2.4right).]
Максимальную полезную мощность найдем, используя формулу:
[P_{p max}={I’}^2r={left(frac{varepsilon}{2r}right)}^2cdot r=frac{varepsilon^2}{4r}=frac{varepsilon^2}{4R}left(2.5right).]
Мы получили систему из трех уравнений с тремя неизвестными:
[left{ begin{array}{c}
I’=frac{varepsilon}{2r}, \
I_k=frac{varepsilon}{r}, \
P_{p max}={left(I’right)}^2r end{array}
left(2.6right).right.]
Используя первое и второе уравнения системы (2.6) найдем $I’$:
[frac{I’}{I_k}=frac{varepsilon}{2r}cdot frac{r}{varepsilon}=frac{1}{2}to I’=frac{1}{2}I_kleft(2.7right).]
Используем уравнения (2.1) и (2.2) выразим внутреннее сопротивление источника тока:
[varepsilon=Ileft(R+rright);; I_kr=varepsilon to Ileft(R+rright)=I_krto rleft(I_k+Iright)=IRto r=frac{IR}{I_k-I}left(2.8right).]
Подставим результаты из (2.7) и (2.8) в третью формулу системы (2.6), искомая мощность будет равна:
[P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}.]
Ответ. $P_{p max}={left(frac{1}{2}I_kright)}^2frac{IR}{I_k-I}$
Читать дальше: формула равнодействующей всех сил.
Источник
3.3. Работа и мощность механической системы
3.3.2. Мощность
Скорость совершения работы характеризуется мощностью.
Различают среднюю и мгновенную мощность.
Средняя мощность определяется формулой
〈N〉=AΔt,
где A — работа, совершаемая за время ∆t.
Для вычисления средней мощности также пользуются формулой
N=(F→,〈v→〉)=F→⋅〈v→〉=F〈v〉cosα,
где F→ — сила, совершающая работу; 〈v→〉 — средняя скорость перемещения; α — угол между векторами F→ и 〈v→〉.
В Международной системе единиц мощность измеряется в ваттах (1 Вт).
Мгновенная мощность определяется формулой
N = A′(t),
где A′(t) — производная от функции работы по времени.
Для вычисления мгновенной мощности также пользуются формулой
N=(F→,v→)=F→⋅v→=Fvcosα,
где F→ — сила, совершающая работу; v→ — мгновенная скорость перемещения; α — угол между векторами F→ и v→.
Пример 20. Тело массой 60 г к моменту падения на Землю имеет скорость 5,0 м/с. Определить мощность силы тяжести в этот момент.
Решение. На рисунке показаны направления скорости тела и силы тяжести, действующей на тело.
В задаче задана мгновенная скорость тела; следовательно, мощность, которую необходимо рассчитать, также является мгновенной мощностью. Величина мгновенной мощности силы тяжести определяется формулой
N = mgv cos α,
где mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; v — модуль скорости тела; α = 0° — угол между векторами скорости и силы.
Произведем вычисление:
N=60⋅10−3⋅10⋅5,0⋅1=3,0 Вт.
Пример 21. При скорости 36 км/ч мощность двигателя автомобиля равна 2,0 кВт. Считая, что сила сопротивления движению автомобиля со стороны воздуха и дороги пропорциональна квадрату скорости, определить мощность двигателя при скорости 72 км/ч.
Решение. Мощность двигателя автомобиля определяется силой тяги и скоростью:
N*=Fтягиvcosα,
где Fтяги — величина силы тяги двигателя автомобиля; v — модуль скорости автомобиля при заданной мощности; α = 0° — угол между векторами силы тяги и скорости.
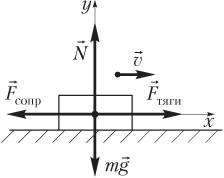
Силы, действующие на автомобиль, направление его скорости и выбранная система координат показаны на рисунке.
Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобиль движется с постоянной скоростью:
F→тяги+F→сопр+mg→+N→=0,
или в проекциях на координатные оси —
Ox: Fтяги−Fсопр=0;Oy: N−mg=0,}
где Fсопр — модуль силы сопротивления движению автомобиля; N — модуль силы нормальной реакции, действующей на автомобиль со стороны дороги; m — масса автомобиля; g — модуль ускорения свободного падения.
Из первого уравнения системы следует равенство модулей сил тяги и сопротивления:
Fтяги = Fсопр.
По условию задачи сила сопротивления пропорциональна квадрату скорости автомобиля:
Fсопр = kv2,
где k — коэффициент пропорциональности.
Подстановка данного выражения в формулу для силы тяги
Fтяги = kv2,
а затем в формулу для вычисления мощности дает:
N*=kv3cosα.
Таким образом, мощность двигателя автомобиля определяется формулой:
- при скорости v1 —
N1*=kv13cosα;
- при скорости v2 —
N2*=kv23cosα,
где v1 = 36 км/ч — первая скорость автомобиля; v2 = 72 км/ч — вторая скорость автомобиля.
Отношение
N1*N2*=kv13cosαkv23cosα=(v1v2)3
позволяет вычислить искомую мощность автомобиля:
N2*=N1*(v2v1)3=2,0⋅103⋅(7236)3=16⋅103 Вт=16 кВт.
Пример 22. Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.
Решение. Мощность двигателей автомобилей определяется формулой:
- для первого автомобиля
N1*=Fтяги1v1cosα,
- для второго автомобиля
N2*=Fтяги2v2cosα,
где Fтяги1 — величина силы тяги двигателя первого автомобиля; v1 — модуль скорости первого автомобиля; Fтяги2 — величина силы тяги двигателя второго автомобиля; v2 — модуль скорости второго автомобиля; α = 0° — угол между векторами силы тяги и скорости.
Силы, действующие на первый и второй автомобиль, направление движения и выбранная система координат показаны на рисунке.
Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобили движутся равноускоренно:
- для первого автомобиля
F→тяги1+m1g→+N→1=m1a→1,
или в проекциях на координатные оси —
Ox: Fтяги1=m1a1;Oy: N1−m1g=0,}
- для второго автомобиля
F→тяги2+m2g→+N→2=m2a→2,
или в проекциях на координатные оси —
Ox: Fтяги2=m2a2;Oy: N2−m2g=0,}
где m1 — масса первого автомобиля; m2 — масса второго автомобиля; g — модуль ускорения свободного падения; N1 — модуль силы нормальной реакции, действующей на первый автомобиль со стороны дороги; N2 — модуль силы нормальной реакции, действующей на второй автомобиль со стороны дороги; a1 — модуль ускорения первого автомобиля; a2 — модуль ускорения второго автомобиля.
Из записанных уравнений следует, что величины сил тяги первого и второго автомобиля определяются формулами:
- для первого автомобиля
Fтяги1 = m1a1,
- для второго автомобиля
Fтяги2 = m2a2.
Отношение модулей сил тяги (Fтяги1/Fтяги2) определяется отношением
Fтяги1Fтяги2=m1a1m2a2.
Движение автомобилей происходит равноускоренно без начальной скорости, поэтому их скорость с течением времени изменяется по законам:
- для первого автомобиля
v1 = a1t,
- для второго автомобиля
v2 = a2t,
где t — время.
Отношение модулей скоростей (v1/v2) определяется отношением величин ускорений (a1/a2):
v1v2=a1a2,
а отношение мощностей —
N1*N2*=Fтяги1v1cosαFтяги2v2cosα=Fтяги1Fтяги2v1v2.
Подставим в полученное отношение выражения для (Fтяги1/Fтяги2) и (v1/v2):
N1*N2*=m1a1m2a2a1a2=m1m2(a1a2)2.
Преобразование формулы с учетом равенства масс автомобилей (m1 = m2 = m) и замены (a1/a2 = v1/v2) дает искомое отношение мощностей:
N1*N2*=(v1v2)2=(2v2v2)2=22=4.
Таким образом, мощность первого автомобиля в 4 раза больше мощности второго автомобиля.
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2018;
проверки требуют 14 правок.
Мо́щность — скалярная физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени[1].
Используемые обозначения[править | править код]
Обычно в формулах механики обозначается символом N.
В электротехнике обычно обозначается символом P — от лат. potestas (сила, мощь, действенность);
Иногда используется символ W (от англ. watt).
Основные формулы[править | править код]
Различают среднюю мощность за промежуток времени :
и мгновенную мощность в данный момент времени:
Интеграл по времени от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:
Единицы измерения[править | править код]
В Международной системе единиц (СИ) единицей измерения мощности является ватт (Вт), равный одному джоулю в секунду (Дж/с). В теоретической физике, астрофизике, в качестве единицы для мощности часто используют эрг в секунду (эрг/с).
Другой распространённой, но ныне устаревшей единицей измерения мощности, является лошадиная сила. В своих рекомендациях Международная организация законодательной метрологии (МОЗМ) относит лошадиную силу к числу единиц измерения, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются»[2].
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с.(мет.) | л. с.(анг.) |
|---|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10−3 | 10−6 | 0,102 | 107 | 1,36⋅10−3 | 1,34⋅10−3 |
| 1 киловатт | 103 | 1 | 10−3 | 102 | 1010 | 1,36 | 1,34 |
| 1 мегаватт | 106 | 103 | 1 | 102⋅103 | 1013 | 1,36⋅103 | 1,34⋅103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81⋅10−3 | 9,81⋅10−6 | 1 | 9,81⋅107 | 1,33⋅10−2 | 1,31⋅10−2 |
| 1 эрг в секунду | 10−7 | 10−10 | 10−13 | 1,02⋅10−8 | 1 | 1,36⋅10−10 | 1,34⋅10−10 |
| 1 лошадиная сила (метрическая) | 735,5 | 735,5⋅10−3 | 735,5⋅10−6 | 75 | 7,355⋅109 | 1 | 0,9863 |
| 1 лошадиная сила (английская) | 745,7 | 745,7⋅10−3 | 745,7⋅10−6 | 76,04 | 7,457⋅109 | 1,014 | 1 |
Мощность в механике[править | править код]
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
где F — вектор силы; v — вектор скорости; — угол между вектором скорости и силы; F — модуль силы; v — модуль скорости.
Частный случай мощности при вращательном движении:
M — момент силы, — угловая скорость, — число пи, n — частота вращения (число оборотов в минуту, об/мин.).
Электрическая мощность[править | править код]
Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность участка электрической цепи:
где — мгновенный ток через участок цепи;
— мгновенное напряжение на этом участке.
При изучении сетей переменного тока, помимо мгновенной мощности, соответствующей общефизическому определению, вводятся также понятия:
- активной мощности, равной среднему за период значению мгновенной мощности,
- мгновенная активная мощность:
- реактивной мощности, которая соответствует энергии, циркулирующей без диссипации от источника к потребителю и обратно,
- мгновенная реактивная мощность:
при
при
- полной мощности, вычисляемой как произведение действующих значений тока и напряжения без учёта сдвига фаз.
- мгновенная полная мощность
где
— амплитуда тока;
— амплитуда напряжения;
— угол между начальным углом напряжения и начальным углом силы тока —
— угловая скорость;
— время.
Приборы для измерения электрической мощности[править | править код]
- Ваттметры (в том числе варметры) — измерительные приборы, предназначенные для определения мощности электрического тока или электромагнитного сигнала. По назначению и диапазону частот ваттметры можно разделить на три категории — низкочастотные (и постоянного тока), радиочастотные и оптические. Ваттметры радиодиапазона по назначению делятся на два вида: проходящей мощности, включаемые в разрыв линии передачи, и поглощаемой мощности, подключаемые к концу линии в качестве согласованной нагрузки. В зависимости от способа функционального преобразования измерительной информации и её вывода оператору ваттметры бывают аналоговые (показывающие и самопишущие) и цифровые.
Гидравлическая мощность[править | править код]
Мощность гидромашины или гидроцилиндра равна произведению перепада давления на машине (разности давлений на входе и выходе) на расход жидкости:
где — расход жидкости, м3/с;
— перепад давления, Па.
К примеру, насос НП-89Д, стоящий на Су-24, Ту-134 и Ту-154, имеет производительность 55 л/мин (~ 0,000917 м3/с) при давлении 210 кгс/см2 (21 МПа)[3] — следовательно, его гидравлическая мощность составляет примерно 19,25 кВт.
См. также[править | править код]
- Удельная мощность
- Активная мощность
- Реактивная мощность
- Светимость
- Энергия
- Мощность взрывного устройства
- Мощность звука
- Усилитель мощности
Примечания[править | править код]
Ссылки[править | править код]
- Электрическая работа и мощность
- Влияние формы электрического тока на его действие. Журнал «Радио», номер 6, 1999 г.
- Гидравлическая мощность и КПД центробежных насосов
Источник
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
Мощность (N) определяют по формуле:
N=At.
Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита («эта») η, он является отношением полезной мощности (N) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше (1), или (100) % (η < 1, или η < (100) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
Источник