Какую полезную работу совершает двигатель за цикл

Физика, 10 класс
Урок 25. Тепловые двигатели. КПД тепловых двигателей
Перечень вопросов, рассматриваемых на уроке:
1) Понятие теплового двигателя;
2)Устройство и принцип действия теплового двигателя;
3)КПД теплового двигателя;
4) Цикл Карно.
Глоссарий по теме
Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.
КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.
Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.
Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.
Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.
Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).
Рабочее тело — тело, которое расширяясь, совершает работу (им является газ или пар)
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 269 – 273.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.
Открытые электронные ресурсы по теме урока
https://kvant.mccme.ru/1973/12/teplovye_mashiny.htm
Теоретический материал для самостоятельного изучения
Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.
Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.
Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.

Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.
Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.
Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.
В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.
В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.
Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.
Для определения эффективности работы теплового двигателя вводят понятие КПД.
Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.


Q1 – количество теплоты полученное от нагревания 
Q2 – количество теплоты, отданное холодильнику 
 – работа, совершаемая двигателем за цикл.
– работа, совершаемая двигателем за цикл.
Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.
Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле

Передача неиспользуемой части энергии холодильнику.
В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).
Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т1, и холодильником с температурой Т2, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов
Цикл Карно — самый эффективный цикл, имеющий максимальный КПД.
Не существует теплового двигателя, у которого КПД = 100% или 1.
Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.
Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.
Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.
Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.
Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.
Сравним эксплуатационные характеристики тепловых двигателей.
КПД:
Паровой двигатель – 8%.
Паровая турбина – 40%.
Газовая турбина – 25-30%.
Двигатель внутреннего сгорания – 18-24%.
Дизельный двигатель – 40– 44%.
Реактивный двигатель – 25%.
Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.
Примеры и разбор решения заданий
1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?
Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м3, s = 100 км = 105 м, ɳ = 25% = 0,25, ρ = 700 кг/м3, q = 46 × 106 Дж/кг.
Найти: N.
Решение:
Запишем формулу для расчёта КПД теплового двигателя:

Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:

Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:

Учитывая всё это, мы можем записать:

Время работы двигателя можно найти по формуле:

Из формулы КПД выразим среднюю мощность:
 .
.
Подставим числовые значения величин:

После вычислений получаем, что N=60375 Вт.
Ответ: N=60375 Вт.
2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?
Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.
Найти: Q1.
Решение
 =
= 
 – это количество теплоты, отданное холодильнику
– это количество теплоты, отданное холодильнику


Источник

За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 68.8%
Ответом к заданию 9 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Газ, находящийся в теплоизолированном цилиндре с подвижным поршнем, получает от нагревателя количество теплоты, равное 200 Дж. Поршень при этом, преодолевая сопротивление 800 Н, переместился на 10 см. Насколько изменилась внутренняя энергия газа? В ответе запишите на сколько (Дж).
Решение
Дано:
$Q=200$Дж
$F=800$Н
$∆x=0.1$м
$∆U-?$
Решение:
Запишем I начало термодинамики: $Q=A+∆U$(1), где $A=F·∆x$(2) — работа газа, $∆U$ — изменение внутренней энергии газа. Тогда из (1) с учетом (2) имеем: $∆U=Q-A=Q-F·∆x=200-800·0.1=200-80=120$Дж.
Ответ: 120
Задача 2
В цилиндре под поршнем находится 2 кг воздуха (M = 0,029 кг/моль) при 20◦С под давлением 1 МПа. Чему равна работа при изобарном нагревании воздуха до 100◦С? Ответ выразите в (кДж), округлив до десятых.
Решение
Дано:
$m=2$кг
$μ=0.029$кг/моль
$t_1=20°C$
$t_2=100°C$
$p=10^6$Па
$R=8.31$Дж/моль·К
$A-?$
Решение:
Работа воздуха определяется выражением: $A=p·∆V$(1), где $p$ — давление, $∆V$ — изменение объема цилиндра (воздуха).
Запишем уравнение Менделеева-Клайперона: $p∆V={m}/{μ}R∆T$(2), учитывая, что $∆T=∆t=t_2-t_1=100°C-20°C=80K$.
Подставим (2) в (1), получим: $A=p·∆V={m}/{μ}R∆T={2·8.31·80}/{0.029}=45848.275=45.8$кДж.
Ответ: 45.8
Задача 3
Температуры нагревателя и холодильника у идеального двигателя соответственно равны 427◦C и 27◦C . Какую работу совершает двигатель за один цикл, если он получает от нагревателя в течение цикла количество теплоты равное 7000 Дж? Ответ выразите в (кДж).
Решение
Дано:
$t_н=427°C$
$t_х=27°C$
$Q_н=7000$Дж
$A-?$
Решение:
КПД двигателя определяется выражением: $η={T_н-T_x}/{T_н}={A}/{Q_н}$(1), где $T_н=t_н+273K=427+273=700K; T_x=t_x+273=27+273=300K$, абсолютные температуры нагревателя и холодильника. Из (1) выразим работу двигателя А: $A={(T_н-T_x)·Q_н}/{T_н}={(700-300)·7000}/{700}=4000=4$кДж.
Ответ: 4
Задача 4
Какую работу совершит газ, расширяясь при постоянном давлении 304 кПа от объёма 3 л до объёма 18 л? Ответ выразите в (кДж).
Решение
Дано:
$p=304·10^3$Па
$V_1=3·10^{-3}м^3$
$V_2=18·10^{-3}м^3$
$A-?$
Решение:
Работа газа определяется выражением: $A=p·∆V=p·(V_2-V_1)=304·10^3·(18·10^{-3}-3·10^{-3})=304·10^3·15·10^{-3}=4560=4.56$кДж.
Ответ: 4.56
Задача 5
В закрытом сосуде под поршнем находится водяной пар при температуре 100◦С под давлением 40 кПа. Каким станет давление пара в сосуде, если объём пара в нём изотермически уменьшить в 1,5 раза за счёт движения поршня? Ответ выразите в (кПа).
Решение
Дано:
$T_1=100°С$
$P_1=40$кПа
$T=const$
$V_2={V_1}/{1.5}$
$P_2-?$
Решение:
По закону Менделеева-Клайперона $P_1·V_1=P_2·V_2⇒P_2={P_1·V_1}/{V_2}=40·1.5=60$кПа.
Ответ: 60
Задача 6
Тепловая машина имеет КПД 25%. Найдите среднюю мощность передачи теплоты холодильнику, если рабочее тело машины за 10 с получает от нагревателя 30 кДж теплоты. Ответ выразите в (кВт).
Решение
Дано:
$η=0.25$
$t=10c$
$Q_н=30$кДж
$P_x-?$
Решение:
$P_н={Q_н}/{t}={30}/{10}=3$кВт.
$η={P_н-P_x}/{P_н}·100$.
$P_x=P_н-η·P_н=3-0.75=2.25$кВт.
Ответ: 2.25
Задача 7
КПД двигателя внутреннего сгорания равен 60%. Определите температуру в камере сгорания двигателя, если температура струи, выходящей из его сопла, составляет 727◦С. Ответ выразить в (K).
Решение
Дано:
$η=0.6$
$T_{вых}=727+273=1000К$
$T_н-?$
Решение:
$η={T_н-T_x}/{T_н}$ для тепловой машины определяем $T_н$.
$0.6={T_н-1000}/{T_н}; T_н={1000}/{0.4}=2500K$.
Ответ: 2500
Задача 8
У работающего по циклу Карно теплового двигателя температура нагревателя 400 К, а температура холодильника 150 К. Найдите коэффициент полезного действия этого двигателя. Ответ выразите в (%).
Решение
Дано:
$T_н=400K$
$η-?$
$T_x=150K$
Решение:
Для цикла Карно справедливо уравнение $η={T_н-T_x}/{T_н}·100%={400-150}/{400}·100%=62.5%$
Ответ: 62.5
Задача 9
Температура нагревателя 177◦С. Определите температуру холодильника, если известно, что коэффициент полезного действия этого двигателя равен 45%. Ответ выразите в (К).
Решение
Дано:
$T_н=177°C$
$η=45%$
$T_x-?$
Решение:
Из теории о теплообмене $η={T_н-T_x}/{T_н}·100%$
$0.45={177-T_x}/{177}$. Нельзя, т.к. $T_н=177+273=450K$
$0.45={450-T_x}/{450}⇒T_x=247.5K$
Ответ: 247.5
Задача 10
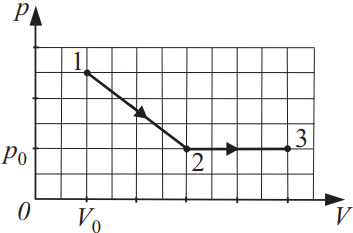
На рисунке показана зависимость давления идеального газа от его объёма при переходе из состояния 1 в состояние 2, а затем в состояние 3. Найдите, чему равно отношение работ газа ${A_{12}}/{A_{23}}$.
Решение
Дано:
${A_{12}}/{A_{23}}-?$
Решение:
Воспользуемся соотношением площадей под графиком ${S_{12}}/{S_{23}}={14}/{8}=1.75$.
Ответ: 1.75
Задача 11
Тепловая машина с КПД 60% за цикл работы отдаёт холодильнику 100 Дж теплоты. Какое количество теплоты за цикл получает машина от нагревателя? Ответ выразите в (Дж).
Решение
Дано:
$η=60%$
$Q_x=100$Дж
$Q_н-?$
Решение:
1) Из теории о тепловых машинах $η={Q_н-Q_x}/{Q_н}·100%$.
$100=Q_н·0.4$
$0.6=1-{100}/{Q_н}$
$Q_н=250$Дж
Ответ: 250
Задача 12
Идеальный газ совершил работу 100 Дж и отдал при этом количество теплоты 300 Дж. Как изменилась при этом внутренняя энергия? В ответе запишите на сколько уменьшилась (Дж).
Решение
Дано:
$A=100$Дж
$Q=-300$Дж
Решение:
По первому началу термодинамики $∆U=A+Q=100+300=400$Дж. Газ отдает тепло и совершает $А$, $∆U$ — уменьшается.
Ответ: 400
Задача 13
Рабочее тело тепловой машины за один цикл получает от нагревателя теплоту 1000 Дж. Температура нагревателя 500 К, температура холодильника 200 К. Какую работу совершает рабочее тело за один цикл? Ответ выразите в (Дж).
Решение
Дано:
$Q_н=1000$Дж
$T_н=500$К
$T_x=200$К
Решение:
$A=Q_н-Q_x$
$η={T_н-T_x}/{T_н}={Q_н-Q_x}/{Q_н}$ по формуле из основы теплообмена.
$A={(T_н-T_x)Q_н}/{T_н}={300·1000}/{500}=600$Дж.
Ответ: 600
Задача 14
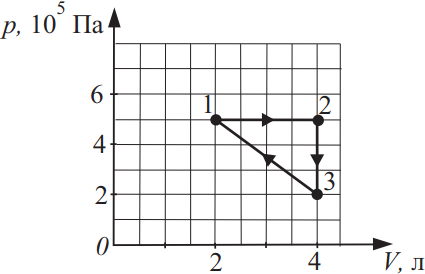
Вычислите работу идеального газа при совершении им кругового процесса, изображённого на рисунке. Ответ выразите в (Дж).
Решение
Дано:
$А-?$
Решение:
Из графика очевидно: $A=A_{12}+A_{23}+A_{31}$
$A_{23}=0$, т.к. нет изменения $V$.
$A_{12}=p∆V=5·10^5·2·10^{-3}=10^3$
$A_{31}={1}/{2}(2·10^5+5·10^5)·2·10^{-3}=-7·10^2$
$A=A_{12}-A_{31}=1000-700=300$Дж.
Ответ: 300
Задача 15
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразить в (кДж).
Решение
Дано:
$Q=10$кДж
$∆U=30$кДж
$A-?$
Решение:
Первое начало термодинамики говорит о том, что количество $Q$ сообщенное системе, идет на приращение внутренней энергии и на совершении работы над внешними телами $Q=∆U+A$
$A=Q-(-∆U)=10+30=40$кДж
Ответ: 40
Задача 16
Двигатель внутреннего сгорания совершил работу, равную 27,6 МДж, и израсходовал при этом 3 л бензина. Вычислите КПД двигателя. Удельная теплота сгорания бензина равна 44 МДж/кг. Плотность бензина равна 700 кг/м3. Ответ округлите до целого. Ответ выразите в (%).
Решение
Дано:
$A_n=27.6$МДж
$m_б=ρ_б·v_б$
$v_б=3$л
$r=44$МДж/кг
$ρ_б=700$кг/м$^3$
$η-?$
Решение:
$η={A_п}/{A_з}$ — полезная и затраченная работа.
$A_з=Q$(сгорание бензина)$=r·m_б=r·ρ_б·v_б$.
$η={27.6·10^6}/{44·10^6·100·3·10^{-3}}·100%=30%$
Ответ: 30
Задача 17
В цилиндре под поршнем находится гелий. Газ расширился при постоянном давлении, совершив работу 3 кДж. Какое количество теплоты сообщили газу? Ответ выразите в (кДж).
Решение
Дано:
$A=3·10^3$Дж
$i=3$
$Q-?$
Решение:
Запишем I начало термодинамики для изобарного процесса (p=const): $Q=A+∆U$(1), где $A=p·∆V$(2), $∆U={i}/{2}υR∆T$(3) — изменения внутренней энергии гелия. Исходя из уравнения Менделеева-Клайперона: $p·∆V=υR∆T$(4), $∆U={i}/{2}p·∆V={i}/{2}A$(5). Подставим (5) в (1): $Q=A+{i}/{2}A=A(1+{i}/{2})$(6). Подставим числовые значения в (6): $Q=3·10^3(1+{3}/{2})=7.5кДж$
Ответ: 7.5
Задача 18
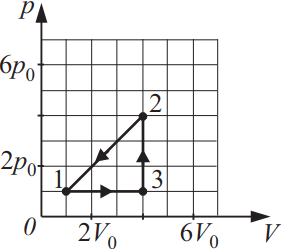
Работа газа в круговом процессе равна 900 кДж. Рассчитайте значение объёма V0, если давление p0 = 105 Па. Ответ выразите в (м3).
Решение
Дано:
$p_0=10^5$Па
$A=9·10^5$Дж
$V_0-?$
Решение:
Работа газа в термодинамике численно равна площади фигуры кругового процесса. Найдем эту площадь: $A={(p_2-p_1)·(V_3-V_1)}/{2}$(1)
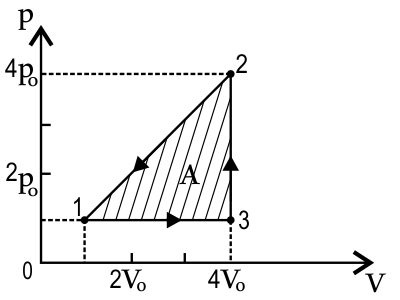
Подставим: $p_2=4p_0; p_1=p_0; V_3=4V_0; V_1=V_0$
$A={(4p_0-p_0)·(4V_0-V_0)}/{2}$
$2A=3p_0·3V_0$
$2A=9p_0V_0$
$V_0={2A}/{9p_0}$(2)
Подставим числовые значения в (2): $V_0={2·9·10^5}/{9·10^5}=2м^3$
Ответ: 2
Задача 19
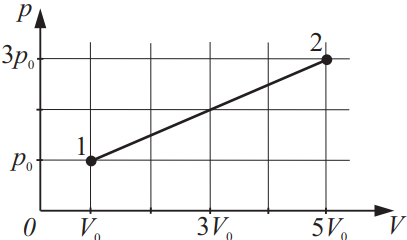
Рассчитайте работу газа при переходе из состояния 1 в состояние 2, если давление p0 = 105 Па, а объём V0 = 1 м3. Ответ выразите в (кДж).
Решение
Дано:
$p_0=10^5$Па
$V_0=1м^3$
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
$A_{12}-?$
Решение:
Поскольку работа газа в термодинамике численно равна площади под графиком, т.е. площади трапеции.
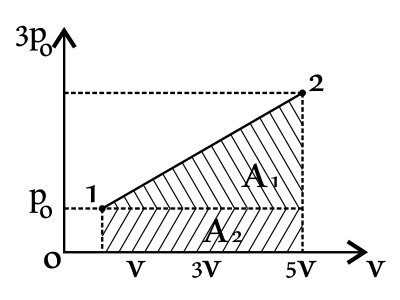
Тогда имеем: $A_{12}=A-1+A_2={(3p_0-p_0)·(5V_0-V_0)}/{2}+(p_0-0)·(5V_0-V_0)={2p_0·4V_0}/{2}+p_0·4V_0=4p_0V_0+4p_0V_0=8p_0V_0$(1)
Подставим числовые значения в (1): $A_{12}=8·10^5·1=8·10^5=800$кДж.
Ответ: 800
Задача 20
Температура нагревателя идеальной тепловой машины в два раза больше температуры холодильника. Каков термический КПД цикла? Ответ выразите в (%).
Решение
Дано:
$T_н=2T$
$T_x=T$
$η-$
Решение:
КПД цикла определяется по формуле: $η={T_н-T_x}/{T_н}·100%$(1), $T_н$ — температура нагревателя, $T_x$ — температура холодильника.
$η={2T-T}/{2T}·100%={T·100%}/{2T}=50%$
Ответ: 50
Источник

