Мощность станка и коэффициент полезного действия
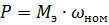
КПД станка (ηст) показывает, какая часть потребляемой мощности используется на полезную работу – резание и равен произведению КПДэлементов кинематической цепи, участвующих в передаче движения от электродвигателя до шпинделя (потери мощности в механизме подач учитываются отдельным коэффициентом), КПД станка рассчитывается по формуле:
,
где η1– КПД ременной передачи, η1 = 0,97
η2– КПД пары зубчатых передач, η2 = 0,98;
η3– КПД подшипников качения, η3 = 0,995;
η4–КПД подшипников скольжения, η4 = 0,985;
a,b,c,d– соответственно количество элементов в кинематической цепи, по которой осуществляется главное движение;
k– коэффициент, учитывающий потери мощности в механизме подач. Для токарных станков k = 0,96.
Пример:
На задней ступени участвуют следующие кинематические пары:
1. Клиноременная передача (3 ремня)
2.В коробке скоростей 3 зубчатых пары, 9 подшипников качения и1 подшипник скольжения.
ηст. = 0,9730,983 0,9959 0,96 = 0,91 0,94 0,96 0,985 0,96 = 0,825
Крутящий момент
В процессе резания необходимо сохранить условие:
Мщп. ≥ Мрез.,
где Мщп.– крутящий момент на шпинделе, кГм;
Мрез.– крутящий момент, необходимый для осуществления процесса резания при заданных режимах, кГм.
Крутящий момент на шпинделе для каждой ступени определяется в зависимостиот числа оборотов шпинделя (nшп.), числа оборотов электродвигателя (nэд.), его мощности(N, кВт),КПД станка (ηст.).
, кГм;
где Мэд.– крутящий момент на валу электродвигателя, кГм;
где nэд.– число оборотов вала электродвигателя, об/мин.
При положении рукояток в коробке скоростей Д–3, Ж–1, Е–1 передаточное отношение от электродвигателя до шпинделя составит
отсюда
Продольная подача
Величина продольной подачи рассчитывается по уравнению
Sпр. = 1/об·iобщ.·π·m·z, мм/об.
где iобщ.–общее передаточное отношение механизмов от шпинделя до
реечной шестерни;
z–число зубьев реечной шестерни;
m–модуль реечной шестерни;
π·m·z–длина делительной окружности реечной шестерни.
В кинематической цепи от шпинделя до реечной шестерни участвуют следующие механизмы: трензель (тр.), гитара смешенных шестерен (гит.), коробка подач (к.п.), механизм фартука суппорта(ф.), реечная пара.
iобщ. = iтр.·iгит.·iк.п.·iф.
Изменение величины подачи осуществляется за счет изменения передаточных отношений ступеней коробки передач. Передаточные отношения остальных механизмов, в т.ч. и гитары, остаются постоянными.
Пример:
Рассчитать продольную подачу при положении шестерён и рукояток в коробке передач: А–1, Б–1, В–5.
iтр. = или с промежуточной шестернёй ;
iгит. =
iк.п. =
iфартука, включая постоянные шестерни блокировочного механизма (рукоятка Г):
iф. =
Длина делительной окружности реечной шестерни
π·m·z= 3·3,14·14= 132 мм,
где m–модель реечной шестерни, равней 3 мм;
z– число зубьев реечной шестерни, равное 14.
Следовательно, для заданного положения настройки коробки передач
Поперечная подача
Перемещение поперечных салазок суппорта Sпоп.осуществляется при помощи винтовой пары, винт которой кинематически связан со шпинделем станка.
Расчет подачи производится по уравнению:
Sпоп. = 1/об·iобщ.·tв.п., мм/об.
где iобщ.–общеее передаточное отношение механизмов от шпинделя до винта поперечной подачи;
tв.п.– шагвинта поперечной подачи, мм.
В кинематической цепи участвуют механизмы трензеля, гитары, коробки подач, фартука и винтовой пары.
iобщ. = iтр.·iгит.·iк.п.·iф.
Величина подачи изменяется за счет коробки подач, передаточные отношения остальных механизмов остается постоянными.
Пример:
Рассчитать поперечную подачу при положении шестерён и рукояток в коробке подеч: А–1, Б–1, В–5.
iтр. = или с промежуточной шестернёй ;
iгит. =
iк.п. =
iф. =
Шаг винта поперечной подачи tв.п. = 5мм.
Следовательно, для заданного положения шестерен и рукоятоккоробки подач
Метрическая резьба.
Общее уравнение кинематической цепи при настройке станка для нарезания резьбы: tн.р. = iтр.·iгит.·iк.п.·tх.в.
где tх.в.– шаг ходового винта станка, мм;
tн.р.– шаг нарезаемой резьбы, мм.
Пример:
Рассчитать шаг метрической резьбы при положении шестерён и рукояток коробки подач: А–2, Б–1,В–5.
Сменные шестерни гитары 48–127–110–44.
Дюймовый шаг винта выражаем в миллиметрах:
tх.в.
tн.р. = iтр.·iгит.·iк.п.·tх.в. =
Дюймовая резьба
Определить число ниток при нарезании дюймовой резьбы (Кн.р.).
Положение рукояток коробки подач: А–2, Б–1, В–1.
Сменные шестерни гитары: 24–127–48.
tн.р. = iтр.·iгит.·iк.п.·tх.в.
tн.р. и tх.в. выражаем через число ниток на дюйм (Кн.р. и Кх.в.)
tн.р. =
tх.в. =
Значения tн.р. и tх.в. подставляем в уравнение кинематическойцепи:
=iтр.·iгит.·iк.п.·
После преобразования и сокращения
tх.в. = ½;
Кх.в. = 2 витка на 1 дюйм.
нитки на 1 дюйм.
Расчёт вести в простых дробях.
Содержание отчета
В отчет должны быть включены: цель работы, расчёты (согласно заданного варианта) крутящего момента,продольной подачи,поперечной подачи,метрической и дюймовой резьбы.
Контрольные вопросы
1. На примере кинематической схемы рассказать устройство основных узлов токарно-винторезного (или др. заданного) станка.
2. Объяснить принцип расчёта крутящего момента.
3. Объяснить принцип расчёта продольной подачи.
4. Объяснить принцип расчёта поперечной подачи.
5. Объяснить принцип расчёта метрической и дюймовой резьбы.
Источник
общей тягой 3, длину которой можно регулировать гайкой 2, устанавливая тем самым необходимый зазор между колодками и шкивом 7 для холостого положения. В процессе торможения колодки стягиваются тягой 4 от приводного механизма 5. Ленточный тормоз (рисунок 27, 6} работает по тому же принципу, что и колодочный. Приводным механизмом здесь является электромагнит или соленоид 1. многодисковый тормоз (рисунок 27, в) работает следующим образом. На приводном валу расположены две многодисковые фрикционные муфты: муфта 1 привода и тормозная муфта 4. Скользящая между ними на шпонке фасонная втулка 3 в момент пуска перемещается влево и своей конической поверхностью поворачивает рычаги 2, которые перемещают нажимной диск муфты 1 влево и включают ее. При перемещении втулки 3 вправо включается тормозная муфта 4, а приводная муфта выключается.
КРИВОШИПНО-КУЛИСНЫЕ МЕХАНИЗМЫ
Кривошипно-кулисные механизмы применяют для преобразования вращательного движения в прямолинейное возвратно-поступательное.

Кривошипный привод (рисунок 28, а) работает следующим образом. От вращающегося кривошипного диска 1 с ради-ально-подвижным пальцем 2 движение через раздвижной шатун 3, качающийся рычаг с зубчатым сектором 4 передается круглой рейке 5, закрепленной на шпинделе 6. за счет радиального перемещения пальца 2 можно регулировать величину хода шпинделя 6, а изменением длины шатуна 3 — крайние положения инструмента, закрепленного в шпинделе. Кривошипный привод применяется, например, в зубодол-бежных станках.
Кулисный привод. Кривошипное зубчатое колесо 1 (рисунок 28, б) получает вращение и через палец 2 сообщает качательное движение рычагу 3, который шарнирно связан с ползуном 4, совершающим возвратно-поступательное движение. Величину хода ползуна 4 регулируют изменением положения пальца 2 на зубчатом колесе 1.
Кулисный привод находит широкое применение в долбежных и поперечно-строгальных станках. Он обеспечивает хорошую плавность движения рабочего органа станка, однако имеет неравномерную скорость рабочего хода и постоянное соотношение между временем рабочего и холостого ходов.
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРИВОДА СТАНКА
КПД привода станка определяется отношением эффективной мощности резания, необходимой на обработку детали, к общей потребляемой станком мощности при установившемся режиме работы:

где Мэф — эффективная мощность резания; Nc — мощность, затрачиваемая на преодоление вредных сопротивлений в механизмах станка.
Величина КПД зависит от полезной нагрузки, частоты вращения, кинематической схемы привода, конструкции его элементов и качества их изготовления. Так как исполнительные механизмы в большинстве случаев приводятся в движение от электродвигателя с помощью промежуточных звеньев передаточного механизма, то полный КПД станка зависит от промежуточных звеньев станка. Для станков с вращательным главным движением при однодвигательном приводе общий КПД станка находится в пределах 0,75-0,85. Величину КПД отдельных кинематических цепей определяют как произведение КПД промежуточных кинематических пар
![]()
Так подсчитывается КПД привода передачи, когда осуществляется передача полной мощности (если Кэф=0, то и т/Ю, так как не какой полезной работы не совершается). Подсчет КПД отдельных кинематических пар ведут для того же диапазона мощностей, что и для всего привода передачи. Величина КПД привода зависит от частоты вращения передачи. При ее увеличении КПД обычно сначала увеличивается, а затем начинает уменьшаться. Это связано с тем, при увеличении скорости увеличиваются потери на трение, могут появляться удары в передачах, вибрации, повышение деформации и т. д. Тогда КПД можно определить экспериментально или по эмпирическим формулам. Главным средством повышения КПД привода станка является улучшение смазки передач, применение точных передач, сокращение длины кинематических цепей и др.
Величина КПД для цепей подач у станков, где привод главного движения и движения подачи осуществляются от общего электродвигателя, не имеет существенного значения. Это связано с тем, что мощность, используемая на движение подачи по сравнению с мощностью, затрачиваемой на привод главного движения, невелика и составляет в универсальных станках 2-3%.
АСИНХРОННЫЕ ЭЛЕКТРОДВИГАТЕЛИ
Подавляющее большинство металлорежущих станков приводится в движение асинхронными электродвигателями трехфазного тока. Они отличаются простотой, надежностью и малой стоимостью.

Конструктивные формы асинхронных электродвигателей определяются способом их крепления и формой защиты от воздействия окружающей среды. Электродвигатель нормального исполнения на лапах показан на рисунке 29, а. Широко применяют фланцевые электродвигатели (рисунок 29, б) для горизонтальной и вертикальной установок. Пример встроенного электродвигателя приведен на рисунке 30. В этом случае валом электродвигателя служит один из валов станка (часто шпиндель).
Применяемые в станках электродвигатели имеют различные формы защиты от воздействия окружающей среды. Для предотвращения внутрь электродвигателя посторонних предметов, а также для соблюдения техники безопасности электродвигатели имеют решетки. У некоторых электродвигателей делают вентиляционные отверстия, обращенные к низу или расположенные в вертикальных плоскостях, для защиты от попадания жидкости. Ряд
электродвигателей изготавливают без вентиляционных отверстий, т. е. закрытыми. Однако они имеют тот недостаток, что вследствие плохого охлаждения их мощность значительно меньше, чем мощность электродвигателей с защитными устройствами таких же размеров. Выпускают закрытые обдуваемые электродвигатели, у которых имеется наружный вентилятор, закрытый клапаном, прикрывающий конец вала электродвигателя, противоположный шкиву. Обдуваемые электродвигатели наиболее часто применяют в станках.

Рисунок 30. Встроенный электродвигатель шлифовального станка
Электродвигатели рассчитаны на напряжение 127, 220 и 380 В. один и тот же электродвигатель можно включать в сети с разными напряжениями, отличающимися в л/3 раз, например, в сети с напряжением 127 и 220, 220 и 380 В. При этом для меньшего из этих двух напряжений статор электродвигателя включают треугольником, для большего — звездой. Ток в фазовых обмотках электродвигателя в обоих случаях будет при таком включении один и тот же. Кроме того, выпускают электродвигатель на 500 В. Обмотка статора электродвигателей для напряжения 500 В включается на постоянное соединение звездой.

Рисунок 31. Электрошпиндель на подшипниках качения:
1 — пакет статорного железа; 2 — задний щит; 3 — обмотка статора; 4 — пакет жести ротора; 5 — корпус; 6 —
передний щит; 7 — шпиндель
Асинхронные электродвигатели с короткозамкнутым ротором выпускают с номинальной мощностью 0,6-100 кВт на синхронные частоты вращения 600, 700, 1000, 1500, 3000 об/мин. Частоту вращения асинхронного электродвигателя можно повысить, увеличив частоту переменного тока. При шлифовании отверстий малого
диаметра для получения необходимой скорости резания нужны очень высокие частоты вращения шлифовальных шпинделей. Например, при шлифовании кругом диаметром до 3 мм со скоростью 30 м/с частота вращения шпинделя должна быть равна 200 000 об/мин. Для этих целей часто применяют так называемые электрошпиндели (рисунок 31). Электрошпиндель представляет собой шлифовальный шпиндель с встроенным асинхронным короткозамкнутым электродвигателем повышенной частоты. Широко используют электродвигатели на подшипниках с воздушной смазкой.
Механическая характеристика электродвигателя — это зависимость частоты вращения п от момента М на его валу
Электродвигатели бывают с мягкой, жесткой и абсолютно жесткой механической характеристикой. У электродвигателей с мягкой характеристикой изменение момента вызывает значительное изменение частоты вращения его вала. Если это изменение не влечет за собой заметного изменения частоты вращения, характеристика называется жесткой. При абсолютно жесткой характеристике частота вращения электродвигателя не зависит от нагрузки.
Механическая характеристика электродвигателя характеризуется скольжением s, которое выражает относительное снижение частоты вращения электродвигателя при переходе от холостого хода (М=0) к наибольшей (критической) нагрузке (М=МК):

где п0 — скорость вращения магнитного поля (синхронная частота вращения электродвигателя), 1/с и об/мин; п — частота вращения ротора (асинхронная).
Скольжение электродвигателя выражается в процентах или долях единицы.
 Момент асинхронного электродвигателя приближенно может быть определен по формуле
Момент асинхронного электродвигателя приближенно может быть определен по формуле
где Мк — критический (наибольший нагрузочный) момент электродвигателя; sk — критическое скольжение, соответствующее моменту Мк.

На рисунке 32 показаны механические характеристики асинхронного электродвигателя, построенные по формуле крутящего момента. При п=п0 момент М=0. Этот случай синхронного вращения соответствует идеальному холостому ходу машины. В первый момент пуска электродвигателя, когда ротор еще неподвижен и s=l, электродвигатель развивает пусковой (начальный) момент Мп, который больше номинального момента Мн. Значения Мк и sk определяют критическую точку (максимум) механической характеристики.
Источник
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
Мощность (N) определяют по формуле:
N=At.
Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита («эта») η, он является отношением полезной мощности (N) к полной или общей мощности Nполная.
Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
η=AAполная⋅100%.
Коэффициент полезного действия всегда меньше (1), или (100) % (η < 1, или η < (100) %).
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
Источник
Ïðè ðàñ÷åòå ìîùíîñòè ýëåêòðîäâèãàòåëÿ ñ ðåãóëèðîâàíèåì ñêîðîñòè íåîáõîäèìî ó÷èòûâàòü ìåõàíè÷åñêóþ õàðàêòåðèñòèêó ìåõàíèçìà.
Äëÿ ìåõàíèçìà ãëàâíîãî äâèæåíèÿ, ãäå îñóùåñòâëÿåòñÿ äâóõçîííîå ðåãóëèðîâàíèå ñêîðîñòè: ñ ïîñòîÿííûì ìîìåíòîì è ïîñòîÿííîé ìîùíîñòüþ, ìîùíîñòü ýëåêòðîäâèãàòåëÿ ðàññ÷èòûâàåòñÿ ïî ôîðìóëå
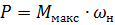
ãäå: Ììàêñ — ìàêñèìàëüíîå ñîïðîòèâëåíèå ïðè ïðîäîëæèòåëüíîé íàãðóçêå è ìàêñèìàëüíîå ýêâèâàëåíòíîå ñîïðîòèâëåíèå ïðè ïîâòîðíî-êðàòêîâðåìåííîé íàãðóçêå; ωí — ìàêñèìàëüíàÿ ñêîðîñòü ïðè ðåãóëèðîâàíèè ñ ïîñòîÿííûì ìîìåíòîì (ïðè íîìèíàëüíîì ïîòîêå).
Äëÿ ïðèâîäà ïîäà÷ ìîùíîñòü îïðåäåëÿåòñÿ, èñõîäÿ èç ìàêñèìàëüíîãî ýêâèâàëåíòíîãî ìîìåíòà è ìàêñèìàëüíîé ñêîðîñòè. Ïðè áîëüøîì äèàïàçîíå ðåãóëèðîâàíèÿ ñêîðîñòè öåëåñîîáðàçíî ïðèìåíÿòü ýëåêòðîäâèãàòåëè ñ íåçàâèñèìîé âåíòèëÿöèåé èëè çàêðûòîãî òèïà. Ïðè ïðèìåíåíèè ýëåêòðîäâèãàòåëÿ ñ ñàìîâåíòèëÿöèåé íåîáõîäèìî ó÷èòûâàòü óõóäøåíèå åãî îõëàæäåíèÿ íà ìàëûõ ñêîðîñòÿõ.
Äëÿ íåðåãóëèðóåìûõ äâèãàòåëåé, êàê ïðàâèëî, ðàáîòàþùèõ â ðåæèìå S6 (åñëè öèêë íå ïðåâûøàåò 10 ìèí) ðàñ÷åò ìîùíîñòè îñóùåñòâëÿåòñÿ ñëåäóþùèì îáðàçîì.
Ìîùíîñòü ýëåêòðîäâèãàòåëÿ äëÿ êàæäîé îïåðàöèè îïðåäåëÿåòñÿ ïî ôîðìóëå:
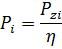
ãäå: Pzi, η — ìîùíîñòü ðåçàíèÿ è êïä ñòàíêà ñîîòâåòñòâåííî.
Êïä â çàâèñèìîñòè îò íàãðóçêè îïðåäåëÿåòñÿ, èñõîäÿ èç ïîòåðü ìîùíîñòè, ïðèíèìàÿ çà îñíîâó âûðàæåíèå:
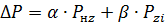
ãäå: Ðíz — íîìèíàëüíàÿ ìîùíîñòü ðåçàíèÿ; α è β — êîýôôèöèåíòû ïîñòîÿííûõ è ïåðåìåííûõ ïîòåðü.
Ñ ó÷åòîì êîýôôèöèåíò çàãðóçêè
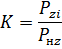
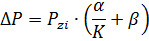
Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ñòàíêà
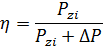
Äëÿ ñëó÷àÿ Ê=1
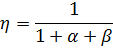
Ðàçäåëåíèå ïîòåðü äëÿ îïðåäåëåíèÿ êïä ïðè ëþáîé íàãðóçêå äàåò
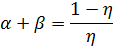
Îðèåíòèðîâî÷íî äëÿ ïðàêòè÷åñêèõ ðàñ÷åòîâ ïðèíèìàåòñÿ
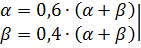
Äëÿ ïðèâîäîâ ãëàâíîãî äâèæåíèÿ òîêàðíûõ, ôðåçåðíûõ, ñâåðëèëüíûõ ñòàíêîâ êïä ïðè ïîñòîÿííîé íàãðóçêå ñîñòàâëÿåò 0,7…0,8, äëÿ øëèôîâàëüíûõ ñòàíêîâ 0,8…0,9. Ìîùíîñòü ýëåêòðîäâèãàòåëÿ ïðè õîëîñòîì õîäå ñòàíêà îïðåäåëÿåòñÿ ïî ôîðìóëå:
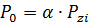
Ïðîäîëæèòåëüíîñòü îïåðàöèè äëÿ êàæäîãî ïåðåõîäà îïðåäåëÿåòñÿ ïî ôîðìóëå:
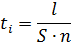
ãäå: l — äëèíà ïåðåõîäà, ìì; S — ïîäà÷à, ìì/îá; n — ñêîðîñòü âðàùåíèÿ øïèíäåëÿ, îá/ìèí.
Âðåìÿ íà óñòàíîâêó è ñíÿòèå äåòàëè ïðèíèìàåòñÿ ðàâíûì 1-3 ìèí. Ïî ðàñ÷åòíîé ìîùíîñòè è âðåìåíè äëÿ êàæäîé îïåðàöèè ñòðîèòñÿ íàãðóçî÷íàÿ äèàãðàììà è îïðåäåëÿåòñÿ ýêâèâàëåíòíàÿ ìîùíîñòü.

Ïðè ïðèìåíåíèè ýëåêòðîïðèâîäà ñ ðåãóëèðîâàíèåì ñêîðîñòè ïðè âûáîðå äâèãàòåëÿ ïî ìîùíîñòè áåðåòñÿ íàèáîëåå òÿæåëûé ðåæèì ðàáîòû, êàê ïî íàãðóçêå, òàê è ïî ÷àñòîòå âêëþ÷åíèé â ÷àñ.
Ïðåäâàðèòåëüíûé âûáîð ýëåêòðîäâèãàòåëÿ â ýòîì ñëó÷àå ïðîèçâîäÿò ïî ýêâèâàëåíòíîìó ìîìåíòó ñ ó÷åòîì êîýôôèöèåíòà çàïàñà íà äèíàìèêó â ïðåäåëàõ Kä=1,1-1,5 è íàèáîëåå âåðîÿòíîé ïðîäîëæèòåëüíîñòè âêëþ÷åíèÿ.
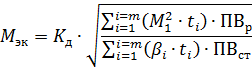
ãäå: βi — êîýôôèöèåíò, ó÷èòûâàþùèé óõóäøåíèå îõëàæäåíèÿ ýëåêòðîäâèãàòåëÿ íà i-ì èíòåðâàëå ïðè ñíèæåíèè ñêîðîñòè íèæå íîìèíàëüíîé;
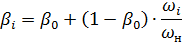
βî- êîýôôèöèåíò óõóäøåíèÿ òåïëîîòäà÷è ïðè íåïîäâèæíîì ÿêîðå; ÏÂÐ, ÏÂñò — ðàñ÷åòíîå è ñòàíäàðòíîå çíà÷åíèå ïðîäîëæèòåëüíîñòè âêëþ÷åíèÿ.
Ìîùíîñòü äâèãàòåëÿ îïðåäåëÿåòñÿ èç ôîðìóëû
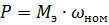
Çàòåì ïðîèçâîäèòñÿ ïðîâåðêà íà ïåðåãðóçî÷íóþ ñïîñîáíîñòü è íà íàãðåâ ñ ó÷åòîì ðåàëüíîãî ìîìåíòà èíåðöèè äâèãàòåëÿ, çàãîòîâêè è ìåõàíè÷åñêèõ ÷àñòåé ñòàíêà.
Источник

