Может ли сила трения совершать полезную работу
В специальном разделе физики — динамике, когда изучают движение тел, то рассматривают действующие на движущуюся систему силы. Последние могут выполнять как положительную, так и отрицательную работу. Рассмотрим в данной статье, что такое работа силы трения и как она рассчитывается.
Понятие работы в физике
В физике понятие «работа» отличается от обыденного представления об этом слове. Под работой понимают физическую величину, которая равна скалярному произведению вектора силы на вектор перемещения тела. Предположим, что имеется некоторый объект, на который действует сила F¯. Поскольку другие силы не действуют на него, то вектор его перемещения l¯ будет по направлению совпадать с вектором F¯. Скалярное произведение этих векторов в данном случае будет соответствовать произведению их модулей, то есть:
A = (F¯*l¯) = F*l.
Величина A — это работа силы F¯ по перемещению объекта на расстояние l. Учитывая размерности величин F и l, получаем, что работа измеряется в ньютонах на метр (Н*м) в системе СИ. Однако, единица Н*м имеет собственное название — это джоуль. Это означает, что концепция работы совпадает с концепцией энергии. Иными словами, если сила в 1 ньютон перемещает тело на 1 метр, то соответствующие энергетические затраты равны 1 джоулю.
Что такое сила трения?
Изучение вопроса работы силы трения возможно, если знать, о какой силе идет речь. Трением в физике называется процесс, который препятствует любому движению одного тела по поверхности другого, когда эти поверхности приведены в контакт.
Если рассматривать исключительно твердые тела, то для них существует три вида трения:
- покоя;
- скольжения;
- качения.
Эти силы действуют между соприкасающимися поверхностями и всегда направлены против движения тел.
Трение покоя препятствует возникновению самого движения, трение скольжения проявляет себя в процессе движения, когда поверхности тел скользят друг по другу, а трение качения существует между телом, которое катится по поверхности, и самой поверхностью.
Примером действия трения покоя является автомобиль, который стоит на ручном тормозе на склоне холма. Трение скольжения проявляет себя при движении лыжника по снегу или конькобежца по льду. Наконец, трения качения действует во время движения колеса автомобиля по дороге.
Силы для всех трех видов трения вычисляются по следующей формуле:
Ft = µt*N.
Здесь N — реакции опоры сила, µt — коэфициент трения. Сила N показывает величину воздействия опоры на тело перпендикулярно плоскости поверхности. Что касается параметра µt, то он измеряется экспериментальным путем для каждой пары трущихся материалов, например, дерево-дерево, сталь-снег и так далее. Измеренные результаты собраны в специальные таблицы.
Для каждой силы трения коэффициент µt имеет собственное значения для выбранной пары материалов. Так, коэффициент трения покоя больше такового для трения скольжения на несколько десятков процентов. В свою очередь, коэффициент качения на 1-2 порядка меньше такового для скольжения.
Работа сил трения
Теперь, познакомившись с понятиями работы и с видами трения, можно переходить непосредственно к теме статьи. Рассмотрим по порядку все виды сил трения и разберемся, какую работу они выполняют.
Начнем с трения покоя. Этот вид проявляет себя тогда, когда тело не движется. Поскольку нет движения, значит, вектор его перемещения l¯ равен нулю. Последнее означает, что работа силы трения покоя также равна нулю.
Трение скольжения по своему определению действует только тогда, когда тело перемещается в пространстве. Поскольку сила этого вида трения направлена всегда против перемещения тела, значит, она совершает отрицательную работу. Величину A можно рассчитать по формуле:
A = -Ft*l = -µt*N*l.
Работа силы трения скольжения направлена на замедление движения тела. В результате совершения этой работы механическая энергия тела переходит в тепло.

Трение качение, как и скольжение, также предполагает движение тела. Сила трения качения совершает отрицательную работу, замедляя исходное вращение тела. Поскольку речь идет о вращении тела, то значение работы этой силы удобно вычислять через работу ее момента. Соответствующая формула записывается в виде:
A = -M*θ, где M = Ft*R.
Здесь θ — угол поворота тела в результате вращения, R — расстояние от поверхности до оси вращения (радиус колеса).
Задача с силой трения скольжения
Известно, что деревянный брусок находится на краю наклонной деревянной плоскости. Плоскость к горизонту наклонена под углом 40o. Зная, что коэффициент трения скольжения равен 0,4, длина плоскости равна 1 метр, и масса бруска соответствует 0,5 кг, необходимо найти работу трения скольжения.
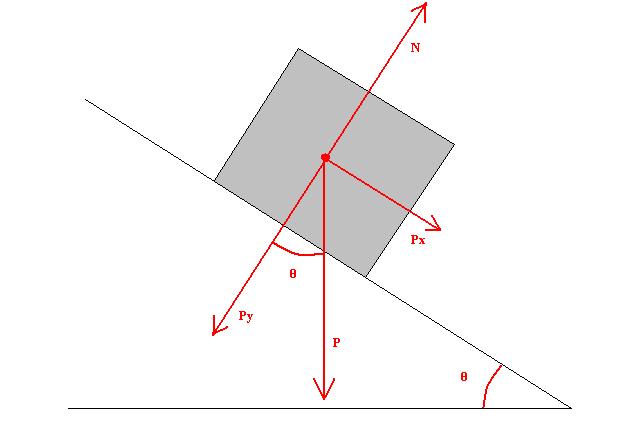
Рассчитаем силу трения скольжения. Она равна:
Ft = m*g*cos(α)*µt = 0,5*9,81*cos(40o)*0,4 = 1,5 Н.
Тогда соответствующая работа A будет равна:
A = -Ft*l = -1,5*1 = -1,5 Дж.
Задача с силой трения качения
Известно, что колесо прокатилось по дороге некоторое расстояние и остановилось. Диаметр колеса равен 45 см. Количество оборотов колеса до остановки равно 100. Принимая во внимание коэффициент качения равный 0,03, необходимо найти, чему равна работа силы трения качения. Масса колеса равна 5 кг.

Сначала вычислим момент силы трения качения:
M = Ft*R = µt*m*g*D/2 = 0,03*5*9,81*0,45/2 = 0,331 Н*м.
Если количество оборотов, сделанных колесом, умножить на 2*pi радиан, то мы получим угол поворота колеса θ. Тогда формула для работы имеет вид:
A = -M*θ = -M*2*pi*n.
Где n — число оборотов. Подставляя момент M и число n из условия, получаем искомую работу: A = — 207,87 Дж.
Источник
На данном уроке мы узнаем, в чём заключается закон сохранения энергии и что такое полная механическая энергия. Также мы рассмотрим работу ещё одной механической силы, которая называется сила трения скольжения, и обобщим знания обо всех трёх разновидностях сил в природе
Введение
В механике рассматриваются два вида энергии: кинетическая и потенциальная. Кинетическая энергия связана с движением тела, потенциальная – со взаимодействием тел или частей одного и того же тела. На этом уроке мы получим ответ на вопрос: какую практическую ценность несёт в себе понятие энергия?
Закон сохранения механической энергии
Тела, взаимодействующие только друг с другом, образуют замкнутую систему тел. Она может обладать кинетической и потенциальной энергией, которые могут изменяться с течением времени.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком.
,
где – потенциальная энергия в конечный момент времени; – потенциальная энергия в начальный момент времени.
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел.
,
где – кинетическая энергия в конечный момент времени; – кинетическая энергия в начальный момент времени.
Приравняем два выражения:
Из данной формулы видно, что кинетическая и потенциальная энергия системы изменяются синхронным образом, то есть увеличение одной приведёт к уменьшению другой, и эти изменения равны друг другу с точностью до знака (происходит превращение энергии из одной разновидности в другую). Следовательно, сумма потенциальной и кинетической энергии является величиной постоянной, называемой полной механической энергией.
Для примера, в системе тел, в которой действует сила тяжести (система «Земля – падающее тело» или «Земля – брошенное вверх тело») (см. Рис. 1), полная механическая энергия равна:
Рис. 1. Тела, взаимодействующие силами тяжести
Если между телами системы действует сила упругости (см. Рис. 2), то полная механическая энергия запишется так:
Рис. 2. Между телами системы действует сила упругости
Равенство значений полной механической энергии в начальный и конечный момент времени означает, что полная механическая энергия замкнутой системы тел не меняется с течением времени, то есть сохраняется. В этом состоит суть закона сохранения механической энергии:
Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остаётся неизменной при любых движениях тел системы.
Многие задачи с использованием этого закона решаются намного проще, чем при прямом решении уравнения движения, то есть при использовании второго закона Ньютона, так как в этом случае используются лишь конечный и начальный момент времени.
В современной теоретической физике доказывается, что закон сохранения механической энергии является следствием фундаментального свойства нашего мира, так называемой однородности времени. Это свойство заключается в том, что любые моменты времени равноправны между собой.
Работа силы трения
В земных условиях сила трения в той или иной мере проявляется при всех движениях тела. Эта сила возникает лишь при относительном движении соприкасающихся друг с другом тел и направлена противоположно скорости тела. Именно этим она отличается от других сил.
Если толкнуть тело, которое лежит на горизонтальной поверхности, то оно будет двигаться против силы трения. Кинетическая энергия при этом уменьшается (см. Рис. 3). Пройдя какое-то расстояние, тело остановится и обратно двигаться не будет. Следовательно, кинетическая энергия, уменьшаясь, в потенциальную не переходит.
Рис. 3. Движение тела, под действием силы трения
Можно сделать вывод: если тело движется под действием силы трения, даже в присутствии других сил, то закон сохранения полной механической энергии не выполняется. Полная механическая энергия уменьшается вместе с кинетической энергией.
Рассмотрим пример с падением тела (см. Рис. 4). Учтём, что тело падает не в пустоте, а в воздухе. При этом потенциальная энергия также уменьшается на mgh, как при падении в вакууме, но скорость тела при достижении земли будет меньше той скорости, которое приобрело бы тело в случае отсутствия воздуха, следовательно, меньше будет и кинетическая энергия тела. Таким образом, увеличение кинетической энергии не будет равно уменьшению потенциальной. Уменьшение полной механической энергии произошло из-за работы силы сопротивления, а сила сопротивления во многом аналогична силе трения.
Рис. 4. Падение тела в воздухе и вакууме
Обобщающие выводы относительно трёх основных разновидностей сил в природе
Силы тяжести и упругости
Работа силы тяжести и силы упругости равна взятому с обратным знаком изменению потенциальной энергии. Данная работа не зависит от формы траектории, а определяется только начальным и конечным положением тела, именно этот факт позволяет для этих сил ввести понятие потенциальной энергии, поэтому данные силы называют потенциальными или консервативными. Если в замкнутой системе действуют только такие силы, то полная механическая энергия такой системы сохраняется.
Силы трения
Работа силы трения зависит от формы траектории. Для этой силы работу нельзя выразить через изменение какой-то величины, которую можно назвать потенциальной энергией. Силы, для которых не имеет смысла вводить понятие потенциальной энергии, называются диссипативными.
Трение двух тел друг о друга приводит к их нагреванию. Увеличение температуры приводит к увеличению внутренней энергии тела. Следовательно, при движении тела под действием силы трения кинетическая энергия переходит в его внутреннюю энергию, то есть происходит переход механической энергии в немеханические формы энергии. Измерения показывают: несмотря на несохранение механической энергии при наличии трения, сохраняется полная энергия, которая учитывает и немеханические формы, в частности внутреннюю энергию тел системы. Следовательно, закон сохранения энергии имеет фундаментальный характер, если под энергией понимать полную энергию тел системы, то есть сумму всех видов энергий.
Итоги урока
На этом уроке мы установили, что для замкнутой системы тел, в которой действуют только консервативные силы, выполняется закон сохранения механической энергии. Если в замкнутой системе действуют также и диссипативные силы, то закон сохранения механической энергии нарушается, но тем не менее остаётся справедливым закон сохранения полной энергии замкнутой системы тел.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- Касьянов В.А. Физика. 10 кл.: Учебн. для общеобразоват. учеб. заведений. – М.: Дрофа, 2000.
Домашнее задание
- Вопросы в конце параграфа 50 и 51 (стр. 130 и 132); – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы) (Источник)
- Камень массой 1 кг брошен вертикально вверх с начальной скоростью 4 м/с. На сколько увеличится потенциальная энергия камня от начала движения к тому времени, когда скорость камня уменьшится до 2 м/с?
- Мальчик столкнул санки с вершины горки. Высота горки – 10 м, у ее подножия скорость санок равнялась 15 м/с. Трение санок о снег пренебрежимо мало. Какой была скорость санок сразу после толчка?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Its-physics.org (Источник).
- Интернет-портал Sch119comp2.narod.ru (Источник).
- Интернет-портал Fizportal.ru (Источник).
Источник
Мякишев Г.Я., Кондрашева Л., Крюков С. Работа сил трения //Квант. — 1991. — № 5. — С. 37-39.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Сила трения, как и любая другая сила, совершает работу и соответственно изменяет кинетическую энергию тела при условии, если точка приложения силы перемещается в выбранной системе отсчета. Однако сила трения существенно отличается от других, так называемых консервативных, сил (тяготения и упругости), так как ее работа зависит от формы траектории. Вот почему работу сил трения ни при каких обстоятельствах нельзя представить в виде изменения потенциальной энергии системы. Кроме того, дополнительные сложности при вычислении работы создает специфика силы трения покоя. Здесь существует ряд стереотипов физического мышления, которые хотя и лишены смысла, но очень устойчивы.
Мы рассмотрим несколько вопросов, связанных с не вполне правильным пониманием роли силы трения в изменении энергии системы тел.
О силе трения скольжения
Нередко говорят, что сила трения скольжения всегда совершает отрицательную работу и это приводит к увеличению внутренней (тепловой) энергии системы.
Такое утверждение нуждается в важном уточнении — оно справедливо только в том случае, если речь идет не о работе одной отдельно взятой силы трения скольжения, а о суммарной работе всех таких сил, действующих в системе. Дело в том, что работа любой силы зависит от выбора системы отсчета и может быть отрицательной в одной системе, но положительной в другой. Суммарная же работа всех сил трения, действующих в системе, не зависит от выбора системы отсчета и всегда отрицательна. Вот конкретный пример.
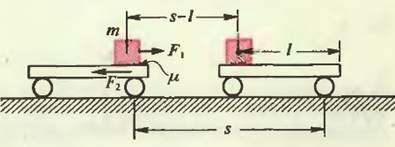
Рис. 1
Положим кирпич на движущуюся тележку так, чтобы он начал по ней скользить (рис. 1). В системе отсчета, связанной с землей, сила трения F1, действующая на кирпич до, прекращения скольжения, совершает положительную работу A1. Одновременно сила трения F2, действующая на тележку (и равная по модулю первой силе), совершает отрицательную работу A2, по модулю большую, чем работа A1, так как путь тележки s больше пути кирпича s — l (l — путь кирпича относительно тележки). Таким образом, получаем
(~A_1 = mu mg(s — l), A_2 = -mu mgs) ,
и полная работа сил трения
(~A_{tr} = A_1 + A_2 = -mu mgl < 0) .
Поэтому кинетическая энергия системы убывает (переходит в тепло):
(~Delta E_k = -mu mgl) .
Этот вывод имеет общее значение. Действительно, работа двух сил (не только сил трения), осуществляющих взаимодействие между телами, не зависит от выбора системы отсчета (докажите это самостоятельно). Всегда можно перейти к системе отсчета, относительно которой одно из тел покоится. В ней работа силы трения, действующей на движущееся тело, всегда отрицательна, так как сила трения направлена против относительной скорости. Но она отрицательна и в любой другой системе отсчета. Следовательно, всегда, при любом количестве тел в системе, Atr < 0. Эта работа и уменьшает механическую энергию системы.
О силе трения покоя
При действии между соприкасающимися телами силы трения покоя ни механическая, ни внутренняя (тепловая) энергия этих тел не изменяется. Значит ли это, что работа силы трения покоя равна нулю? Как и в первом случае, такое утверждение правильно только по отношению к полной работе сил трения покоя над всеми взаимодействующими телами. Одна же отдельно взятая сила трения покоя может совершать работу, причем как отрицательную, так и положительную.
Рассмотрим, например, книгу, лежащую на столе в набирающем скорость поезде. Именно сила трения покоя сообщает книге такую же скорость, как у поезда, т. е. увеличивает ее кинетическую энергию, совершая определенную работу при этом. Другое дело, что такая же по модулю, но противоположная по направлению сила действует со стороны книги на стол, а значит, и на поезд в целом. Эта сила совершает точно такую же работу, но только отрицательную. В результате получается, что полная работа двух сил трения покоя равна нулю, и механическая энергия системы тел не меняется.
О движении автомобиля без проскальзывания колес
Самое устойчивое заблуждение связано именно с этим вопросом.

Рис. 2
Пусть автомобиль вначале покоится, а затем начинает разгоняться (рис. 2). Единственной внешней силой, сообщающей автомобилю ускорение, является сила трения покоя Ftr действующая на ведущие колеса (мы пренебрегаем силой сопротивления воздуха и силой трения качения). Согласно теореме о движении центра масс, импульс силы трения равен изменению импульса автомобиля:
(~F_{tr} Delta t = Delta(M upsilon_c) = M upsilon_c) ,
если скорость центра масс в начале движения равнялась нулю, а в конце υc. Приобретая импульс, т. е. увеличивая свою скорость, автомобиль одновременно получает и определенную порцию кинетической энергии. А поскольку импульс сообщается силой трения, естественно считать, что и увеличение кинетической энергии определяется работой этой же силы. Вот это-то утверждение оказывается совершенно неверным. Сила трения ускоряет автомобиль, но работы при этом не совершает. Как же так?

Рис. 3
Вообще говоря, ничего парадоксального в этой ситуации нет. В качестве примера достаточно рассмотреть совсем простую модель — гладкий кубик с прикрепленной сбоку пружинкой (рис. 3). Кубик, придвигают к стене, сжимая пружинку, а затем отпускают. «Отталкиваясь» от стены, наша система (кубик с пружинкой) приобретает определенные импульс и кинетическую энергию. Единственной внешней силой, действующей по горизонтали на систему, является, очевидно, сила реакции стены Fp. Именно она и сообщает системе ускорение. Однако никакой работы при этом, конечно, не совершается — ведь точка приложения этой силы неподвижна (в системе координат, связанной с землей), хотя сила действует некоторое конечное время Δt.
Аналогичная ситуация возникает и при разгоне автомобиля без проскальзывания. Точка приложения силы трения, действующей на ведущее колесо автомобиля, т. е. точка соприкосновения колеса с дорогой, в любой момент покоится относительно дороги (в системе отсчета, связанной с дорогой). При движении автомобиля она исчезает в одной точке и сразу же появляется в соседней.
Не противоречит ли сказанное закону сохранения механической энергии? Конечно же, нет. В нашем случае с автомобилем изменение кинетической энергии системы происходит за счет ее внутренней энергии, выделяющейся при сгорании топлива.
Для простоты рассмотрим чисто механическую систему: игрушечный автомобиль с пружинным заводом. Двигатель такого автомобиля использует не внутреннюю энергию топлива, а потенциальную энергию сжатой пружины. Вначале пружина заведена, и ее потенциальная энергия Ep1 отлична от нуля. Если двигатель игрушки — просто растянутая пружина, то (~E_{p1} = frac{k (Delta l)^2}{2}). Кинетическая энергия равна нулю, и полная начальная энергия автомобиля E1 = Ep1. В конечном состоянии, когда деформация пружины исчезнет, потенциальная энергия равна нулю, а кинетическая энергия (~E_{k2} = frac{M upsilon_c^2}{2}). Полная энергия E2 = Ek2. Согласно закону сохранения энергии (трением мы пренебрегаем),
(~frac{M upsilon_c^2}{2} = frac{k (Delta l)^2}{2}) .
В случае реального автомобиля
(~frac{M upsilon_c^2}{2} = Delta U) ,
где ΔU — энергия, полученная при сгорании топлива.
Если колеса автомобиля проскальзывают, то Atr<0, так как точка соприкосновения колес с дорогой движется против направления силы трения. Следовательно,
(~frac{M upsilon_c^2}{2} = frac{k (Delta l)^2}{2} + A_{tr}) .
Видно, что кинетическая энергия автомобиля в конечном состоянии оказывается меньше, чем в отсутствие проскальзывания.
Источник

