Огэ по математике полезные материалы и шпаргалки

Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.

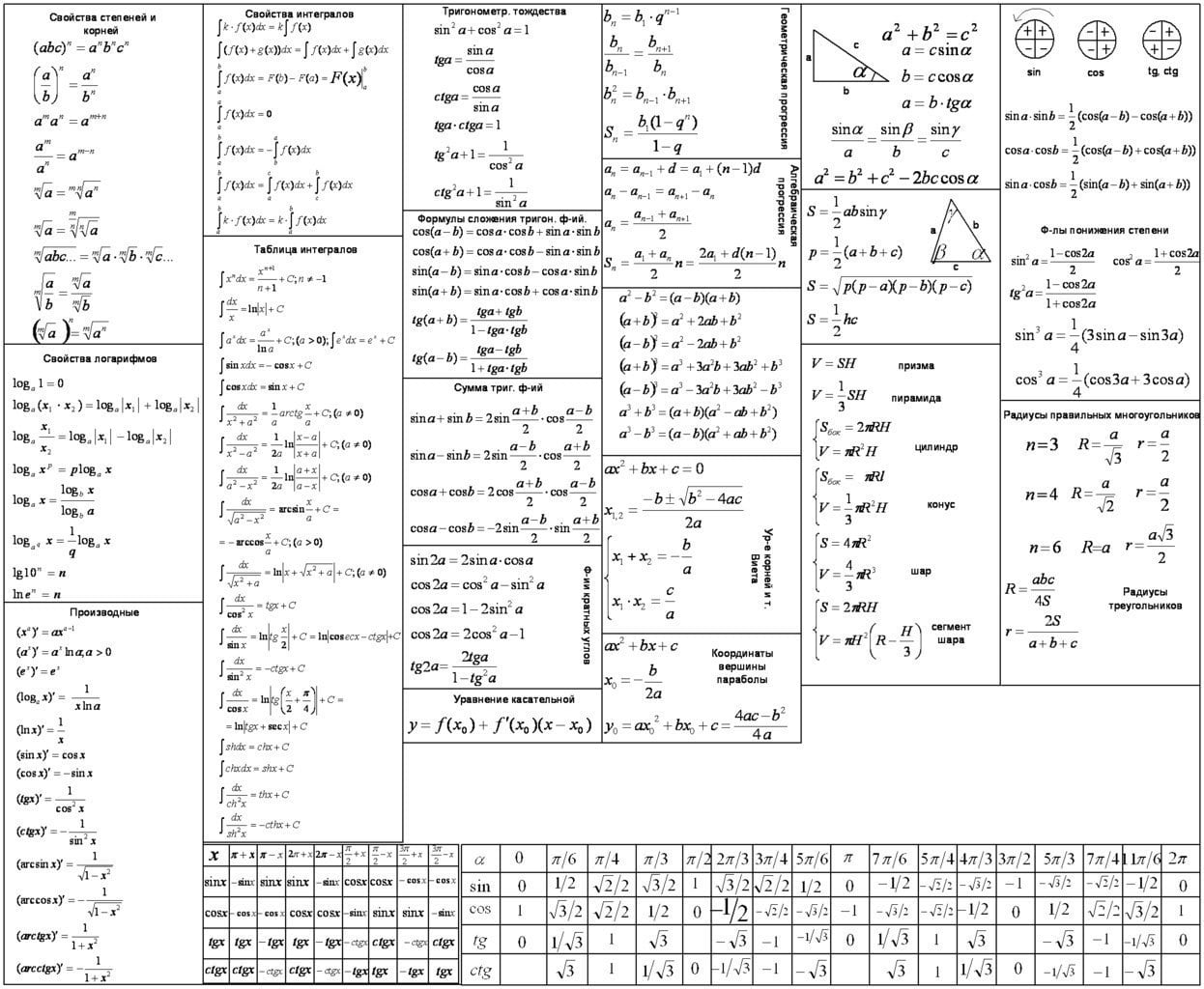
Для начала шпаргалка в компактном виде:

шпаргалки по математике

Формулы сокращенного умножения

(а+b)2 = a2 + 2ab + b2

(а-b)2 = a2 – 2ab + b2

a2 – b2 = (a-b)(a+b)

a3 – b3 = (a-b)( a2 + ab + b2)

a3 + b3 = (a+b)( a2 – ab + b2)

(a + b)3 = a3 + 3a2b+ 3ab2+ b3

(a – b)3 = a3 – 3a2b+ 3ab2- b3

Свойства степеней

a0 = 1 (a≠0)

am/n = (a≥0, n ε N, m ε N)

a- r = 1/ a r (a>0, r ε Q)

a m · a n = a m + n

a m : a n = a m – n (a≠0)

(a m) n = a mn

(ab) n = a n b n

(a/b) n = a n/ b n

Первообразная

Если F’(x) = f(x), то F(x) – первообразная

для f(x)

Функция f(x) = Первообразная F(x)

k = kx + C

xn = xn+1/n+1 + C

1/x = ln |x| + C

ex = ex + C

ax = ax/ ln a + C

1/√x = 2√x + C

cos x = sin x + C

1/ sin2 x = – ctg x + C

1/ cos2 x = tg x + C

sin x = – cos x + C

1/ x2 = – 1/x

Геометрическая прогрессия

bn+1 = bn · q, где n ε N

q – знаменатель прогрессии

bn = b1 · qn – 1 – n-ый член прогрессии

Сумма n-ыхчленов

Sn = (b n q – b 1 )/q-1

Sn = b 1 (q n – 1 )/q-1

Модуль

|a| = a, если a≥0

-a, если a<0

Формулы cos и sin

sin (-x) = -sin x

cos (-x) = cos x

sin (x + π) = -sin x

cos (x + π) = -cos x

sin (x + 2πk) = sin x

cos (x + 2πk) = cos x

sin (x + π/2) = cos x

Объемы и поверхности тел

1. Призма, прямая или наклонная, параллелепипед V = S·h

2. Прямая призмаSБОК = p·h, p – периметр или длина окружности

3. Параллелепипед прямоугольный

V = a·b·c; P = 2(a·b + b·c + c·a)

P – полная поверхность

4. Куб: V = a3 ; P = 6 a2

5. Пирамида, правильная и неправ.

S = 1/3 S·h; S – площадь основания

6. Пирамида правильная S =1/2 p·A

A – апофема правильной пирамиды

7. Цилиндр круговой V = S·h = πr2h

8. Цилиндр круговой: SБОК = 2 πrh

9. Конус круговой: V=1/3 Sh = 1/3 πr2h

10. Конус круговой: SБОК = 1/2 pL= πrL

Тригонометрические уравнения

sin x = 0, x = πn

sin x = 1, x = π/2 + 2 πn

sin x = -1, x = – π/2 + 2 πn

cos x = 0, x = π/2 + 2 πn

cos x = 1, x = 2πn

cos x = -1, x = π + 2 πn

Теоремы сложения

cos (x +y) = cosx ·cosy – sinx ·siny

cos (x -y) = cosx ·cosy + sinx ·siny

sin (x +y) = sinx ·cosy + cosx ·siny

sin (x -y) = sinx ·cosy – cosx ·siny

tg (x ±y) = tg x ± tg y/ 1 -+ tg x ·tg y

ctg (x ±y) = tg x -+ tg y/ 1± tg x ·tg y

sin x ± sin y = 2 cos (x±y/2)· cos (x-+y/2)

cos x ± cosy = -2 sin (x±y/2)· sin (x-+y/2)

1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2

1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2

6. Трапеция

a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h

7. Квадрат

а – сторона, d – диагональ S = a2 = d2/2

8. Ромб

a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα

9. Правильный шестиугольник

a – сторона S = (3√3/2)a2

10. Круг

S = (L/2) r = πr2 = πd2/4

11. Сектор

S = (πr2/360) α

Правила дифференцирования

( f (x) + g (x) )’ = f ’(x) + g’(x)

(k(f(x))’ = kf ’ (x)

(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)

(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)

(xn)’ = nx n-1

(tg x)’ = 1/ cos2 x

(ctg x)’ = – 1/ sin2 x

(f (kx + m))’ = kf ’(kx + m)

Уравнение касательной к графику функции

y = f ’(a) (x-a) + f(a)

Площадь S фигуры, ограниченной прямыми x=a, x=b

S = ∫( f(x) – g(x)) dx

Формула Ньютона-Лебница

∫ab f(x) dx = F(b) – F (a)

t	π/4	π/2	3π/4	π
cos	√2/2		-√2/2	1
sin	√2/2	1	√2/2
t	5π/4	3π/2	7π/4	2π
cos	-√2/2		√2/2	1
sin	-√2/2	-1	-√2/2
t		π/6	π/4	π/3
tg		√3/3	1	√3
ctg	—	√3	1	√3/3

sin x = b x = (-1)n arcsin b + πn

https://5-ege.ru/shpargalki-po-matematike/

cos x = b x = ± arcos b + 2 πn

tg x = b x = arctg b + πn

ctg x = b x = arcctg b + πn

Теоремасинусов: a/sin α = b/sin β = c/sin γ = 2R

Теорема косинусов: с2=a2+b2-2ab cos y

Неопределенные интегралы

∫ dx = x + C

∫ xn dx = (xn+1/n+1) + C

∫ dx/x2 = -1/x + C

∫ dx/√x = 2√x + C

∫ (kx+b) = 1/k F(kx + b)

∫ sin x dx = – cos x + C

∫ cos x dx = sin x + C

∫ dx/sin2 x = -ctg + C

∫ dx/cos2 x = tg + C

∫ x r dx = x r+1/r+1 + C

Логарифмы

1. loga a = 1

2. loga 1 = 0

3. loga (bn) = n loga b

4. log An b = 1/n loga b

5. loga b = log c b/ log c a

6. loga b = 1/ log b a

Градус		30	45	60
sin		1/2	√2/2	√3/2
cos	1	√3/2	√2/2	1/2
tg		√3/3	1	√3
t	π/6	π/3	2π/3	5π/6
cos	√3/2	1/2	-1/2	-√3/2
sin	1/2	√3/2	√3/2	1/2
90	*120*	*135*	*150*	*180*
1	√3/2	√2/2	1/2
	-1/2	-√2/2	-√3/2	-1
—	-√3	-1	√3/3
t	7π/6	4π/3	5π/3	11π/6
cos	-√3/2	-1/2	1/2	√3/2
sin	-1/2	-√3/2	-√3/2	-1/2

Формулы двойного аргумента

cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x

sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x

tg 2x = 2 tg x/ 1 – tg2 x

ctg 2x = ctg 2 x – 1/ 2 ctg x

sin 3x = 3 sin x – 4 sin3 x

cos 3x = 4 cos3 x – 3 cos x

tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x

sin s cos t = (sin (s+t) + sin (s+t))/2

sin s sin t = (cos (s-t) – cos (s+t))/2

cos s cos t = (cos (s+t) + cos (s-t))/2

Формулы дифференцирования

c’ = 0 ()’ = 1/ 2

x’ = 1 (sin x)’ = cos x

(kx + m)’ = k (cos x)’ = – sin x

(1/x)’ = – (1/x2) ( ln x)’ = 1/x

(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a

Площади плоских фигур

1. Прямоугольный треугольник

S = 1/2 a·b (a, b – катеты)

2. Равнобедренный треугольник

S = (a/2)·√ b2 – a2/4

3. Равносторонний треугольник

S = (a2/4)·√3 (a – сторона)

4. Произвольный треугольник

a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2

S = 1/2 a·h = 1/2 a2b sin C =

a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)

5. Параллелограмм

a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α

cos (x + π/2) = -sin x

Формулы tg и ctg

tg x = sin x/ cos x; ctg x = cos x/sin x

tg(-x) = – tg x

ctg(-x) = – ctg x

tg (x + πk) = tg x

ctg (x + πk) = ctg x

tg (x ± π) = ± tg x

ctg (x ± π) = ± ctg x

tg (x + π/2) = – ctg x

ctg (x + π/2) = – tg x

sin2 x + cos2 x =1

tg x · ctg x = 1

1 + tg2 x = 1/ cos2 x

1 + ctg2 x = 1/ sin2 x

tg2 (x/2) = 1 – cos x/ 1 + cos x

cos2 (x/2) = 1 + cos x/ 2

sin2 (x/2) = 1 – cos x/ 2

11. Шар: V=4/3 πR3 = 1/6 πD3

P = 4 πR2 = πD2

12. Шаровой сегмент

V = πh2 (R-1/3h) = πh/6(h2 + 3r2)

SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)

13. Шаровой слой

V = 1/6 πh3 + 1/2 π(r2 + h2)· h;

SБОК = 2 π·R·h

14. Шаровой сектор:

V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе

Формула корней квадратного уравнения

(a≥0, b≥0)

(a≥0)

ax2 + bx + c = 0 (a≠0)

Если D=0, то x = -b/2a (D = b2-4ac)

Если D>0, то x1,2 = -b± /2a

Теорема Виета

x1 + x2 = -b/a

x1 · x2 = c/a

Арифметическая прогрессия

a n+1 = an + d, где n – натуральное число

d – разность прогрессии;

a n= a 1 + (n – 1)·d – формула n-го члена

Сумма n членов

Sn = ((a 1 + a n )/2) · n

Sn = ((2a 1 + (n-1)d)/2) · n

Радиус описанной окружности около многоугольника

R = a/ 2 sin 180/n

Радиус вписанной окружности

r = a/ 2 tg 180/n

Окружность

L = 2 πR S = πR2

Площадь конуса

S БОК = πRL

S КОН= πR(L+R)

Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.

Скачать шпаргалки по математике

Скачать всё это в компактном виде: matematika-shpory.doc.

Рекомендуем:

Источник

какие шпаргалки можно сделать на огэ по математике

Шпаргалки, конечно, могут помочь сдать экзамены. Вот несколько советов по их изготовке.

1) «Обычная шпаргалка»
Берётся обычный лист бумаги, на котором мелким текстом пишутся формулы и ответы на вопросы. Лучше всего разделить лист бумаги на несколько частей, чтобы каждая часть свободно входила в карман.
Списать с такой шпаргалки бывает довольно сложно, т. к. её легко могут заметить учителя. Лучше всего садиться в середине или в конце класса.
2) «Шпаргалка-невидимка»
Берётся два листа бумаги. Один лист подкладываем под второй лист. На верхнем листе ручкой пишите нужные формулы и ответы. На ручку надо нажимать посильнее. Верхний исписанный лист можно выкинуть. На нижнем листе бумаги осталось всё, что вы написали, достаточно лишь поймать лучший угол обзора и списать всё написанное.
3) «На резинке»
Ответ пишется на небольшом листе бумаги, на обратную сторону которого скотчем крепится конец тонкой резинки, другой конец привязывается к руке. При опасном приближении преподавателя бумажка отпускается, на что резинка немедленно реагирует и прячет шпаргалку в рукав.
4) «Калькулятор»
В электронную записную книгу, похожую на калькулятор, заносится нужная информация. На экзаменах, где необходим калькулятор, такая записная книжка особых подозрений не вызывает.
5) «Дискетная»
У дискеты 1.44 необходимо отодвинуть металлическую створку и написать на внутреннем диске нужную информацию ручкой или фломастером. Потом собрать дискету обратно и шпаргалка готова. На экзамене дискета кладется на стол и, когда надо, отодвигается металлическая створка и снизу вращается диск. Дополнительно можно на дискету сверху что-нибудь наклеить, а сбоку сделать разметку, как на линейке, чтобы на вопрос: «Что это такое?» , — можно было уверено сказать: «Новая линейка» .
6) Hands free
К мобильному телефону подключается система Hands free, проводная или Bluetooth. На экзамене делается звонок напарнику, который будет диктовать ответ. Этот способ наиболее удобно использовать девушкам с длинными волосами — волосы закрывают наушник.
7) «Рулонная»
Представляет собой распечатку на туалетной бумаге. Для этого надо набрать мелким шрифтом текст, затем распечатать его на плотной туалетной бумаге. Преимущество способа в том, что на маленьком кусочке можно разместить все вопросы. Если преподаватель заметит списывание, необходимо быстро смотать туалетную бумагу в рулон, показать ее и попроситься выйти. В туалете минут за 5 можно выучить или повторить вопрос. Лучшее место для такой шпаргалки — внутренний карман пиджака или карман брюк.
8) «Плеер»
На плеер записывается нужная информация. На экзамене плеер включается и с помощью плей-листа находится нужный ответ. Но любой плеер и любые наушники на экзаменах вызывают подозрение. Чтобы списать с такой шпаргалки, нужно выбрать позицию ближе к концу класса и рядом с окном. На последнюю парту садиться не рекомендуется. Можно облокотиться на окно, зажать наушники руками и делать вид, что думаешь.
9) «Линейка»
На линейке записываются все нужные вам формулы и ответы. Желательно замаскировать их рисунками или надписями, чтобы проходящий мимо учитель не запалил вас.
10) «Под юбкой»
Вам понадобиться: чулочки, желательно не сильно темные, ручка, бумажка.
Пишем на бумажке шпаргалку и засовываем под чулочки. Во время экзамена скромненько приподнимаем юбку и смотрим.
Шпаргалку рекомендуется класть ближе к гениталиям, т. к. учитель не посмеет смотреть у вас под юбкой.
11) «Шпаргалка для девушек»
Можно написать гелиевой ручкой на ногтях, а затем покрыть ногти прозрачным лаком. Будет смотреться так, как будто ногти просто накрашены синеньким симпатичным цветом.
12) «Калькулятор»
Шпаргалку пишем на задней стороне калькулятора простым карандашом. На экзамене ставим калькулятор на стол и спокойно списываем с него.
13) «Язычок»
В язычок ботинка засовываем шпаргалку. На экзамене специально роняем ручку и нагибаясь за ней смотрим за язычок.

Шпаргалки на ОГЭ и ЕГЭ по математике

Самые необходимые формулы по математике на 1 листе

Самые необходимые формулы на 1 листе

Скачать лист

Источник

Необходимый теоретический материал для сдачи ОГЭ по математике.

Ð£Ð³Ð»Ñ Ð¿ÑÐ¸ Ð¿Ð°ÑÐ°Ð»Ð»ÐµÐ»ÑÐ½ÑÑ Ð¿ÑÑÐ¼ÑÑ Ð¸ ÑÐµÐºÑÑÐµÐ¹ Автор: Чудинова Алена Сергеевна

1.Углы:

Вертикальные углы равны (на рис 1и3; 6и8 и др)

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис 4и6; 1 и 7)

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚(на рис 4 и 7; 1 и6)

Соответственные углы при параллельных прямых и секущей равны. (на рис 3 и 7; 1 и 5 и др)

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника — перпендикуляр опущенный из вершины угла на противоположную сторону

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке

3.Треугольник:

Сумма углов в любом треугольнике 180˚

Средняя линия треугольника — прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны

C:UsersАдминистраторDesktop1.gif Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚)

Равнобедренный треугольник — треугольник
у которого равны две стороны.

Свойства равнобедренного треугольника:
в равнобедренном треугольнике углы при основании равны;

в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

C:UsersАдминистраторDesktop2.gif Равносторонний треугольник — треугольник у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак: по двум равным углам

II признак: по двум пропорциональным сторонам и углу между ними

III признак: по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др. катеты)

Свойства прямоугольного треугольника:

Сумма острых углов прямоугольного треугольника равна 90 градусов $90^{circ}$

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a2+b2=c2

Пифагоровы тройки:

3,4,5

6,8,10

5,12,13

9,12,15

Признаки равенства прямоугольных треугольников

По двум катетам:

По гипотенузе и катету:

По катету и прилежащему острому углу:

По катету и противолежащему острому углу

По гипотенузе и острому углу

Признаки подобия прямоугольных треугольников:

По острому углу

По пропорциональности двух катетов

По пропорциональности катета и гипотенузы

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному:

Высота прямоугольного треугольника: h=ab/c или h= ( где АВ гипотенуза, СЕ высота опущенная на гипотенузу)

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=с/2=mc)

3. Четырехугольники:

Сумма углов в любом четырехугольнике 360 ˚

C:UsersАдминистраторDesktopch012.png Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:

У параллелограмма противолежащие стороны равны и противолежащие углы равны:

Сумма любых двух соседних углов параллелограмма равна 180°:

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:

Каждая диагональ делит параллелограмм на два равных треугольника:

Две диагонали параллелограмма делят его на четыре равновеликих треугольника:

C:UsersАдминистраторDesktopch016.png Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон

Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:

Прямоугольник.

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: d=a

C:UsersАдминистраторDesktopch025.png Трапеция.

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полу сумме.

Равнобокой называется трапеция, у которой боковые стороны равны:

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением:

d² = ab+c².

C:UsersАдминистраторDesktoppic968.png Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность:

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности

Отрезок , соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус, проведенный в точку касания, пересекаются под прямым углом

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

Теорема синусов:

5. Формулы площадей

Треугольник :

S = ½(a ⋅ ha)

S = ½(ab ⋅ sinC)

S = √p(p — a)(p — b)(p — c) (р- полупериметр) Формула Герона:

S=1/2(a⋅b) (прямоугольный треугольник, а,b – катеты)

S= ( равносторонний треугольник)

S= ( R- радиус описанной окружности)

S= (r – радиус вписанной окружности, P – периметр)

Квадрат: S = a ⋅ a = a2

ПрямоугольникS = a ⋅ b

Параллелограмм:

S = a ⋅ ha

S =ab ⋅ sinC

S=1/2 d1·d2· sinC

Ромб : S= 1/2d1·d2

Трапеция :S=1/2(a+b)⋅h(а, b основания трапеции)

Круг: S=π⋅r2

Теория вероятности.

Основная формула для вычисления вероятности события

Огэ по математике полезные материалы и шпаргалки

Ответ не может быть больше 1

Формулы сокращенного умножения:

Признаки делимости (необходимо для сокращения дробей и подбора нового знаменателя)

Признак делимости на 2

Последняя цифра числа должна быть четной — 0,2,4,6,8

Признак делимости на 3

Сумма цифр в данном числе должна быть кратна 3

Признаки делимости на 5

Последняя цифра должна быть 0 или 5

Признак делимости на 9

Сумма цифр в данном числе должна быть кратна 9

Признак делимости на 10

Последняя цифра должна быть 0

Разделить на 10, 100, 1000 и т.д, значит перенести запятую на столько знаков влево, сколько нулей в делителе (пример 256:10000=0,0256; 3,7:10=0,37)

Свойства степеней

an • ak = an+k

= an−k или an : ak = an−k

a =1

(an)k = ank

am × bm = (ab)m
am ÷ bm= Огэ по математике полезные материалы и шпаргалки

Стандартный вид числа: записать число цифрами, поставить запятую после первого числа, сосчитать количество цифр после запятой и записать 10 в той степени сколько цифр после запятой.

Пример: 173 тыс= 173000=1,73·105

Любое квадратное уравнение (степень у икса 2) можно решить через дискриминант (D= b2-4ac, x1,2= Огэ по математике полезные материалы и шпаргалки )

Теорема Виета (применяется когда коэффициент а =1): Огэ по математике полезные материалы и шпаргалки

Неполные квадратные уравнения:

1 вид:

ax2+bx=0 – неполное квадратное уравнение (с=0).

Решение: x (ax+b)=0

x1=0 или ax+b=0

x2=-b/a.

Ответ: 0; -b/a.

2 вид:

ax2-c=0 – неполное квадратное уравнение (b=0);

Решение: ax2=c

x2=c/a.

Если (c/a)<0, то действительных корней нет.

Если (с/а)>0, то имеем два действительных корня: x1= x2= —

Неравенства:

Линейные неравенства решение:

1.переносим слагаемые с неизвестным в одну сторону, числа в другую сторону, знак неравенства сохраняется. Делим обе части неравенства на множитель стоящий возле х. Знак неравенства меняется, если делим обе части неравенства на отрицательное число. И сохраняется, если делим на положительное число

2.чертим координатную прямую, отмечаем точки в порядке возрастания. Точки пустые если знак неравенства , точки жирные если знак неравенства, заштриховываем нужные ответ по знаку неравенства.

3.Записываем ответ. Если точка пустая или бесконечность — скобки круглые, точка жирная — скобка квадратная.

Квадратные неравенства:

Переписываем уравнение, заменяя знак неравенства на знак равно.
Решаем квадратное уравнение любым известным способом.
На координатной прямой расставляем точки в порядке возрастания (пустые или жирные, зависит от знака неравенства в изначальном неравенстве)
В любом из полученных интервалов берем любую удобную для счета точку, подставляем в уравнение, в правой части которого 0,
Определяем знак на промежутке. Расставляем знаки на оставшихся интервалах, чередуя знаки, если не было корней четной степени.
Выбираем нужный интервал соответствовав знаку неравенства
Записываем ответ. Если точка пустая или бесконечность — скобки круглые, точка жирная — скобка квадратная.

Решение системы неравенств:

Решаем отдельно первое неравенство из системы.
Решаем отдельно второе неравенство из системы.
На одной координатной прямой отмечаем получившиеся точки из первого и второго решения в порядке возрастания.

4. Согласна знаку неравенства сверху штрихуем решение первого неравенства, снизу решение второго неравенства.

5. Там где штриховка совпала (снизу и сверху) есть решение всей системы неравенств. Если совпадений нет, то решений системы нет)

Источник