Определить полезная мощность при подъеме груза
§ 1 Повторение формул по теме урока
В этом уроке мы рассмотрим решение задач на расчет механической работы и мощности, коэффициент полезного действия простых механизмов.
Для решения задач нужно знать формулы:
· Механическая работа равна произведению модуля силы на пройденный путь: A = F · s. Мощность равна отношению работы ко времени ее выполнения: N = A / t.
· Потенциальная энергия тела, поднятого над землей, вычисляется по формуле:
Еп = mgh.
· Кинетическая энергия – это энергия движения тела, зависит от скорости движения и массы тела: Ек = m υ2/2.
· Коэффициент полезного действия равен отношению полезной работы ко всей полной совершенной работе: η = Апоез/ Аполн.
· Простые механизмы, используемые для выполнения работы, позволяют получить выигрыш в силе, например, подвижный блок дает выигрыш в силе в 2 раза: Pгруза = 2 · Fприл, но при этом проигрываем в пути также в 2 раза.
§ 2 Решение задач
С помощью рычага груз массой 100 кг был поднят равномерно на высоту 80 см. При этом длинное плечо рычага, к которому приложена сила 600 Н, опустилось на 2 м. Определите коэффициент полезного действия рычага.
Запишем условие задачи: масса груза m = 100 кг, сила F = 600 Н, путь, пройденный грузом s1 = h = 80 см = 0,8 м, путь, пройденный длинным плечом рычага s2 = 2 м. Найти кпд η.
Решение: Чтобы найти кпд, определим полезную и полную работу. Полезная работа – это работа по поднятию груза весом mgна 80 см: Аполез = P · s1 = mgh = 100 кг · 10Н/кг · 0,8 м = 800 Дж. Полная работа – это работа, совершенная силой, приложенной к длинному плечу рычага, Аполн = F · s2 = 600 Н · 2 м = 1200 Дж.
Тогда кпд механизма равен: η = Аполез/ Аполн = 800 Дж / 1200 Дж = 0, 67 = 67%
Какая сила потребуется для равномерного поднятия груза массой 200 кг по наклонной плоскости, имеющей кпд 60%? Высота наклонной плоскости –1,5 м, длина – 10 м.
Запишем условие задачи: масса m = 200 кг, высота наклонной плоскости h= 1,5 м, длина l = 10 м, кпд установки η = 60% = 0,6 в системе СИ. Найти приложенную силу F.
Решение: При помощи наклонной плоскости поднимают груз, то есть совершают работу. Полезная работа равна произведению веса груза mg на высоту h. Полная работа совершается приложенной силой на пути, равном длине наклонной плоскости: Аполн = F · s2 = F · l.
Подставим записанные формулы в формулу коэффициента полезного действия и выразим неизвестную величину – приложенную силу: F равно mgh делим на кпд и l. Вычислим, подставив числовые значения известных величин. Ответ: для подъема груза требуется сила 500 Н.
Водяной насос подает 300 л воды в минуту на высоту 20 м. Определить мощность двигателя насоса, если его кпд равен 80%.
Запишем условие задачи: объем воды V = 300 л = 0,3 м3, время работы t = 1 мин = 60 с, путь, пройденный водой, равен высоте s1 = h = 20 м, плотность воды ρ = 1000 кг/м3, кпд насоса η = 80% = 0,8. Найти мощность двигателя N.
Решение: При помощи насоса совершают работу по поднятию воды. Полезная работа равна произведению веса воды на высоту: Аполез = P · s1 = mgh, массу воды найдем по формуле плотности m = ρ · V = 1000 кг/м3 · 0,3 м3 = 300 кг. Тогда полезная работа составит 60 000 Дж.
Полную работу, совершенную двигателем насоса, можно найти по формуле мощности: Аполн = N · t. Подставим в формулу кпд формулу полной работы и выразим неизвестную мощность: N= Аполез/ кпд и время. Вычислим. Ответ: мощность двигателя насоса 1250 Вт.
Итак, при решении задач на расчет коэффициента полезного действия нужно правильно определить, что является полезной работой и что является полной работой. Для этого можно поставить вопрос: с какой целью применяют тот или иной механизм? Ответ на него позволяет определить полезную работу. Полной работой является работа, совершенная самим механизмом.
§ 3 Важно запоминить
Коэффициент полезного действия – это величина, показывающая долю полезной работы от всей полной совершенной работы. КПД выражают в процентах. При решении задач на расчет коэффициента полезного действия нужно определить полезную работу и полную совершенную работу. КПД механизмов всегда меньше 100%.
Источник
Решение
1.Определяем полезную мощность
Р F
Груз движется поступательно. 2.Определяем скорость подъема груза
3.Необходимое усилие равно весу груза (равномерный подъем)
N=G=3000 H 4.Определяем полезную мощность
P=N∙v=3000∙4=12000 Вт
5.Определяем полную мощность, затрачиваемую мотором
Вт=16 кВт
Ответ: 
16 кВт.
Задача 1.2.2.
Для определения мощности электродвигателя через его шкив перекинута тормозная лента. Один конец ленты удерживается динамометром, а к другому концу прикреплена двухкилограммовая гиря. После запуска двигателя при установившейся угловой скорости п=1850 об/мин динамометр показывает усилие 5 кг. Определить мощность двигателя.
Рисунок 1.2.2
14
Решение
1. Рассмотрим, какие силы действуют на шкив при установившемся равномерном вращении.
Шкив приводится во вращательное движение вращающим моментом Мвр ,
создаваемым двигателем. Кроме того, на шкив действует сила натяжения правой ветви ленты, создаваемая динамометром
Т2=5∙9,81=49 Н
и сила Т1 натяжения левой ветви ленты, создаваемая двухкилограммовой гирей
Т1=2∙9,81=19,6 Н.
2. Определим вращающий момент двигателя. Так как шкив вращается равномерно, то алгебраическая сумма моментов всех сил относительно оси вращения шкива равна нулю:
где 
240 мм=0,24 м – диаметр шкива
3.Переведя угловую скорость 
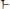
в рад/сек:
4.Определим мощность двигателя:
Ответ: 
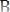
Задача 1.2.3.
Какой мощности электродвигатель необходимо поставить на лебедку, чтобы она могла поднимать клеть со строительными материалами общей массой m=1200кг на высоту 20 м за 30 секунд. Коэффициент полезного действия лебедки равен 0,72.
Решение
1.Полезная мощность, развиваемая лебедкой при подъеме:
2.Мощность двигателя N найдем из выражения к коэффициенту полезного действия
15
3. Таким образом, мощность двигателя, необходимая для лебедки
Ответ: 
.
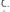
Задача 1.2.4.
Найти усилие натяжения каната, наматываемого на барабан лебедки 3, и определить мощность на приводном валу этого барабана. Канат через неподвижный блок 2 связан с телом 1 (клеть), которое перемещается по направляющим 4 и с ускорением опускается. При этом трением в блоках пренебречь, коэффициент трения скольжения принять f=0,2, удельное сопротивление движению клети ω0=0,01, а угол наклона 
Дано: F=35 кН; v=3,6 м/с; a=2,6 м/с2.
a
Рисунок 1.2.4.
Решение
1.Определяем массу груза:
2.Определяем силу инерции 
, которая направлена противоположно ускорению. А так как ускорение направлено вниз, то груз опускается и сила инерции направлена вверх.
16
Раздел 2. Сопротивление материалов
2.1. Определение нормальных напряжений, построение продольных сил, определение продольных перемещений.
Задача 2.1.1.
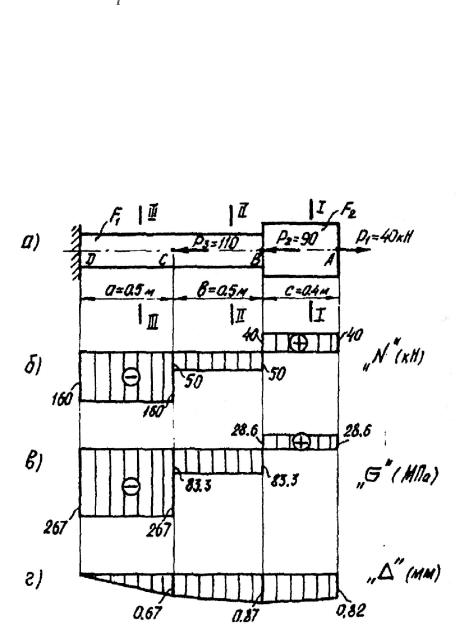
Ступенчатый брус нагружен силами P1, P2, P3 (рис. 2.1.1,а).
Требуется построить эпюры продольных сил N, нормальных напряжений 
, продольных перемещений 
и проверить, выполняется ли условие прочности.
Дано: P1 =40 кН, P2=90 кН, P3 =110 кН, a=0,5 м, b=0,5 м, c=0,4 м, F1=6 см2, F2=14 см2, E=2∙105 МПа, 
240 МПа, nT=1,5.
Решение
1.Построение эпюры N.
На брус действуют три силы, следовательно, продольная сила по его длине будет изменяться. Разбиваем брус на участки, в пределах которых продольная сила будет постоянной. В данном случае границами участков являются сечения, в которых приложены силы. Обозначим сечения буквами A,B,C,D, начиная со свободного конца, в данном случае правого.
Рисунок 2.1.1. Расчетная схема бруса и эпюры:
а– расчетная схема; б – эпюра продольных сил;
в– эпюра напряжений; г – эпюра продольных перемещений
18
Для определения продольной силы на каждом участке рассматриваем произвольное поперечное сечение, начинаем расчеты со свободного конца бруса
А.
Участок АВ, сечение 1-1. Справа от сечения действует растягивающая сила (рис. 2.1.1,а). В соответствии с упомянутым ранее правилом, получаем
Участок ВС, сечение 2-2. Справа от него расположены две силы, направленные в разные стороны. С учетом правила знаков, получим
Участок CD, сечение 3-3: аналогично получаем
По найденным значениям N в выбранном масштабе строим эпюру, учитывая, что в пределах каждого участка продольная сила постоянна (рис. 2.1.1,
б).
Положительные значения N откладываем вверх от оси эпюры, отрицательные – вниз.
2. Построение эпюры напряжений 
.
По формуле вычисляем напряжения в поперечном сечении для каждого участка бруса:
При вычислении нормальных напряжений значения продольных сил N берутся по эпюре с учетом их знаков. Знак плюс соответствует растяжению, минус – сжатию. Эпюра напряжений показана на рис. 2.1.1, в.
3. Построение эпюры продольных перемещений.
Для построения эпюры перемещений вычисляем абсолютные удлинения отдельных участков бруса, используя закон Гука:
19
Определяем перемещение сечений, начиная с неподвижного закрепленного конца. Сечение D расположено в заделке, оно не может смещаться и его перемещение равно нулю:
Сечение C переместится в результате изменения длины участка CD. Перемещение сечения C определяется по формуле
При отрицательной (сжимающей) силе точка C сместится влево. Перемещение сечения В является результатом изменения длин DC и CB.
Складывая их удлинения, получаем
Рассуждая аналогично, вычисляем перемещение сечения А:
В выбранном масштабе откладываем от исходной оси значения вычисленных перемещений. Соединив полученные точки прямыми линиями, строим эпюру перемещений (рис. 2.1.1, г).
4. Проверка прочности бруса.
Условие прочности записывается в следующем виде:
Максимальное напряжение 
находим по эпюре напряжений, выбирая максимальное по абсолютной величине:
Это напряжение действует на участке DC, все сечения которого являются опасными. Допускаемое напряжение вычисляем по формуле:
Сравнивая 
, видим, что условие прочности не выполняется, так как максимальное напряжение превышает допускаемое.
Задача 2.1.2.
Стальной стержень круглого поперечного сечения находится под действием продольной силы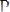 
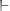
и равномерно распределенной нагрузки 
(рис. 2.1.2). Требуется построить эпюру продольных усилий 
, подобрать сечение
из условия прочности 
и построить эпюру перемещений 
.
Решение
1. В данной задаче необходимо разбить стержень на два участка (рис. 2.1.2). Начиная со свободного конца стержня, мысленно разрезаем каждый участок в
20
Источник
Сборник задач по физике, Лукашик В.И.
785. Какая система, состоящая из двух блоков (см. рис. 222), имеет больший КПД при подъеме грузов одинаковой массы? Ответ объясните.
В системе №2 КПД больше, поскольку в системе №1 производится дополнительная работа по подъему подвижного блока.
786. Используя стальной лом в качестве рычага, на одну и ту же высоту поднимают груз Р двумя способами (рис. 235, а и б). Плечи, на которые действует груз, и трение в точках опоры О одинаковы. Одинаковым ли будет КПД рычагов? Ответ объясните.
В случае «а» КПД больший, так как в случае «б» производится дополнительная работа по подъему лома.
787. Для подъема одного и того же груза на одну и ту же высоту в качестве рычага можно использовать стальной стержень (рис. 236, а) или такого же диаметра и длины, как стержень, стальную трубу (рис. 236, б). Одинаковым ли в этих случаях будет КПД рычагов? Ответ обоснуйте.
Масса стальной трубы меньше, следовательно, работа по ее подъему меньше. Поэтому в случае «б» КПД больше.
788. К короткому плечу рычага (см. рис. 235, б) подвешен груз весом 1200 Н. При равномерном поднятии его на 0,12 м к длинному плечу приложили силу 360 Н, при этом точка приложения силы переместилась на 0,5 м. Вычислите КПД рычага.
789. Вычислите КПД рычага, с помощью которого груз массой 245 кг равномерно подняли на высоту 6 см, при этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения этой силы опустилась на 0,3 м.
790. У какой системы неподвижных блоков (см. рис. 218) при подъеме равных грузов КПД больше, если силы трения в каждом блоке одинаковые? Ответ обоснуйте.
КПД больше у второй системы, поскольку в первой системе больше блоков и больше дополнительная работа против сил трения.
791. Используя одинаковые блоки, можно поднять груз Р на одну и ту же высоту (рис. 237). Одинаковы ли КПД установок? Ответ обоснуйте.
КПД второго блока меньше, поскольку, используя его, необходимо поднимать блок.
792. Ведро, в которое насыпан песок массой 24,5 кг, поднимают при помощи неподвижного блока на высоту 10 м, действуя на веревку силой 250 Н. Вычислите КПД установки.
793. С помощью неподвижного блока груз массой 100 кг поднят на высоту 5 м. Определите совершенную при этом работу, если коэффициент полезного действия равен 70%.
794. У каждого неподвижного блока (рис. 238) КПД равен 0,9. Определите КПД всей установки.
795. Ящик с гвоздями, масса которого 54 кг, поднимают на пятый этаж строящегося дома при помощи подвижного блока, действуя на трос силой 360 Н. Вычислите КПД установки.
796. С помощью блоков равномерно поднимают груз (рис. 239). Используя данные рисунка, вычислите КПД установки.
797. Груз, масса которого 1,2 кг, ученик равномерно переместил к вершине наклонной плоскости длиной 0,8 м и высотой 0,2 м. При этом перемещении сила, направленная параллельно линии наклона плоскости, была равна 5,4 Н. Какой результат должен получить ученик при вычислении КПД установки?
798. При равномерном перемещении груза массой 15 кг по наклонной плоскости динамометр, привязанный к грузу, показывал силу, равную 40 Н. Вычислите КПД наклонной плоскости, если длина ее 1,8 м, высота 30 см.
799. По наклонной плоскости длиной 5 м и высотой 1,5 м поднимается груз массой 180 кг. Чему равны полезная работа и КПД, если коэффициент трений равен 0,3?
800. Двигатель подъемного крана мощностью 6 кВт поднимает груз массой 6 т на высоту 8 м. Определите время подъема груза, если КПД установки равен 80%.
801. Электродвигатель мощностью 10 кВт соединен ременной передачей с насосом, который за 30 мин подает воду в объеме 58,75 м3 на высоту 25 м в резервуар. Определите КПД всей установки.
802. Сколько воды можно поднять из колодца глубиной 36 м в течение 1 ч, если мощность электродвигателя насоса равна 4,9 кВт, а КПД установки равен 70%?
Источник
Рабочая тетрадь по физике 7 класс Т.А. Ханнанова (к учебнику А.В. Перышкина)
Задание 55.1 Заполните пропуски в тексте, используя слова: тело; сила; работа.
Задание 55.2 Штангист совершает различные действия. Поставьте знак «+», если в описанной ситуации штангист совершает над штангой положительную работу, знак «–» – если отрицательную, и число «0», если работа над штангой не совершается.
Задание 55.3 При помощи механизма равномерно поднимают груз вертикально вверх на высоту 2 м, прикладывая силу 500 Н. какую работу при этом совершает приложенная к грузу сила?
Задание 55.4 Мраморную плиту объёмом 2 м3 равномерно поднимают вверх на высоту 4 м с помощью троса. Какую работу при этом совершает сила тяжести, действующая на плиту?
Задание 55.5 Запишите значения работы в указанных единицах.
Задание 55.6 Какую работу совершит мальчик, равномерно переместив санки на расстояние 5 м, прикладывая в горизонтальном направлении силу 3 Н? какую работу при этом совершит сила трения, действующая на санки?
Задание 56.1 Какова средняя мощность силы, если:
Задание 56.2 Выберите правильное утверждение.
Задание 56.3. Сравните мощности двух механизмов, выразив вначале их значения в единицах СИ, а затем поставив между ними подходящие по смыслу знаки.
Задание 56.4. Мощность ракетного двигателя 15 000 кВт. Какую работу он совершает за 10 с полёта?
Задание 56.5. Какую мощность развивает сила при равномерном поднятии груза массой 100 кг на высоту 0,5 м за 0,4 с?
Задание 56.6. Рабочие равномерно тянут тележки разной массы, прикладывая к ним разные силы тяги F1 и F2. На рисунке изображены в масштабе силы, действующие на тележки со стороны рабочих, и скорости тележек. Сравните мощности сил F1 и F2. Ответ поясните.
Задание 56.7. Докажите, что если направление приложенной к телу силы совпадает с направлением скорости этого тела при равномерном движении, мощность этой силы равна
Задание 57.1. Заполните пропуски в тексте.
В быту, строительстве и других видах своей деятельности человек использует различные приспособления, которые позволяют получить выигрыш в силе или просто изменить направление действия силы. Приспособления, служащие для преобразования силы, называются механизмами.
Задание 57.2. Перечислите три простых механизма и приведите примеры их использования.
Задание 58.1. а)Отметьте на рисунках точкой О неподвижную точку рычага (точку опоры). б) Изобразите силы, действующие на рычаг со стороны человека и груза.
Задание 58.2. На каждом рисунке точкой О обозначена точка опоры. покажите плечо каждой силы, действующей на рычаг, и обозначьте его соответственно l1 или l2.
Задание 58.3. На рычаг, находящийся в равновесии, действуют две силы F1 и F2, имеющие плечи l1 и l2 соответственно. Зачеркните все ошибочные алгебраические выражения.
Задание 58.4. В точке А к рычагу подвешено два груза массой по 102 г. Груз какой массы надо подвесить в точке В для того, чтобы рычаг сохранил равновесие?
Задание 58.5. Какую силу показывает динамометр в каждом случае, если рычаг находится в равновесии? Масса каждого груза 102 г.
Задание 59.1. Выберите правильное окончание определения момента силы. Момент силы – это…
произведение модуля силы на плечо этой силы
Задание 59.2. На рисунке показаны рычаги, к которым приложены силы.
Задание 59.3. Выберите правильное утверждение.
Единицей момента силы в СИ является … .
Задание 59.4. Определите момент силы, равной по модулю 40 Н, плечо которой 4 см.
Задание 59.5. На рычаг действуют две силы: 10 Н и 6 Н. плечо каждой силы соответственно равно 24 см и 40 см. первая силы вращает рычаг по ходу часовой стрелки, вторая – против хода часовой стрелки. Находится ли рычаг в равновесии? Ответ обоснуйте.
Задание 60.1. Рабочий удерживает рычаг малой массы в равновесии, прикладывая силу F. На рисунке схематично показаны силы, действующие на рычаг со стороны руки, опоры и груза. Силу тяжести, действующую на рычаг, не учитываем, так как его масса мала. Выполните задания.
Задание 60.2. Человек удерживает на палке груз массой 5 кг. Определите силу давления F палки на плечо. Массой палки пренебречь.
Задание 60.3. Рабочий поднимает груз одинаковой массы с помощью веревки (рис. а) и рычага малой массы (рис. б). Оцените по рисунку, во сколько раз меньшую силу прикладывает рабочий во втором случае, чем в первом.
Задание 60.4. Легкий рычаг находится в равновесии под действием веса груза массой 500 г и силы давления штока АВ поршня, с помощью которого газ удерживается в закрытом сосуде.
Задание 61.1. Заполните пропуски в тексте.
Задание 61.2. Груз какой максимальной массы можно поднять с помощью подвижного лёгкого блока, прикладывая к верёвке силу 200 Н? массой блока пренебречь. Ответ обоснуйте.
Задание 61.3. На рисунке показан подвижный блок, с помощью которого равномерно поднимают груз.
а) На рисунке отметьте точку опоры рычага, соответствующего этому блоку, изобразите действующие на него силы и покажите плечи этих сил.
б) Определите массу груза. Массой блока пренебречь. Ответ обоснуйте.
Задание 61.4. На рисунке показана система из двух блоков, которая часто используется на практике.
Задание 62.1. Рабочий использует неподвижный блок для подъема груза массой 12 кг на высоту 2 м, держа веревку так, что она образует с вертикалью угол 0 0С (рис. а), 45 0С (рис. б) и 60 0С (рис. в). Какую работу совершает рабочий в каждом случае? Ответ поясните.
Задание 62.2. Груз массой 204 г поднимают на высоту 50 см вначале только с помощью нити, а затем с помощью нити и подвижного блока.
Задание 62.3. Двое рабочих равномерно поднимают ведра с раствором, массой 14 кг каждое, с земли на высоту 4 м: первый – стоя на земле, при помощи системы блоков, второй – высунувшись из окна и подтягивая ведро только с помощью веревки.
Задание 63.1. Заполните пропуски в тексте.
Задание 63.2. На рисунке отметьте центр тяжести каждой плоской фигуры, находящийся в точке пересечения диагоналей (рис. а, б), диаметров ( рис. в) или медиан (рис. г).
Задание 63.3.
Проделайте опыт по определению положения центра тяжести треугольника, вырезанного из картона. Подвесьте треугольник на нити за одну из вершин и прикрепите к той же вершине отвес. Проведите вдоль отвеса вертикальную линию на треугольнике. Затем подвесьте фигуру вместе с отвесом за другую вершину, проведите ещё вертикальную линию и обозначьте точку пересечения этих линий (см. рис.). Точка С является центром тяжести картонного треугольника.
Ответьте на вопросы.
Задание 63.4. На рисунках изображены плоские металлические фигуры и отмечены силы тяжести, действующие на их отдельные части.
а) отметьте положение центра тяжести всей фигуры;
б) нарисуйте равнодействующую указанных на рисунке сил — силу тяжести, действующую на всю фигуру, в масштабных единицах.
Задание 63.5. а) Заполните пропуски в тексте.
Задание 64.1. Заполните пропуски в тексте.
Задание 64.2. Обозначьте на каждом рисунке положение центра тяжести тела (точка С) и ось вращения этого тела (точка О). Напишите вид равновесия, в котором находится каждое тело.
Задание 64.3. На рисунке изображён металлический брусок в форме параллелепипеда в двух различных положениях.
а) Определите положение центра тяжести бруска в каждом случае.
б) Нарисуйте положение бруска и его центра тяжести, если брусок привести в неустойчивое равновесие.
в) С помощью транспортира измерьте величину угла поворота, необходимого для приведения бруска в неустойчивое равновесие, и результат запишите около рисунка.
Какое положение бруска является наиболее устойчивым? Ответ объясните.
Задание 64.4.1
Компьютерная модель «Устойчивость тел на плоскости» (см. раздел «Механика» в электронном пособии) позволяет изучить условия устойчивости составного тела из двух поставленных друг на друга кубиков разной плотности.
Проведите два виртуальных эксперимента. В первом опыте сверху расположите кубик плотностью 1 ед. (высотой 30 ед.), а снизу — кубик плотностью 5 ед. (высотой 30 ед.). Во втором опыте кубики разной плотности поменяйте местами. В каждом эксперименте выполните следующие действия.
1. Определите положение центра тяжести составного тела. На рисунке в тетради в масштабе изобразите силы тяжести, действующие на отдельные кубики, и равнодействующую этих сил.
2. На экране монитора постепенно увеличивайте угол наклона плоскости, на которой стоят кубики, до тех пор, пока прямая, вдоль которой направлена равнодействующая сил тяжести, не выйдет за пределы площади опоры и тело не упадёт.
3. Запишите в тетради величину угла поворота, необходимого для приведения составного тела в неустойчивое равновесие, и изобразите это положение тела на рисунке.
Сделайте вывод, в каком случае составное тело из двух кубиков находится в более устойчивом положении.
Задание 64.5. На машине нужно перевезти деревянные и железные бруски одних и тех же размеров. Как следует эти бруски расположить в кузове, чтобы устойчивость машины была наибольшей? Ответ обоснуйте.
Задание 64.6. Какая из приведённых на рисунке конструкций детских ходунков более устойчива? Ответ обоснуйте.
Задание 65.1. Рабочий закатывает тележку массой т = 50 кг на платформу высотой h = 80 см, прикладывая силу F = 125 Н. Длина наклонной плоскости I = 4 м. Определите КПД механизма.
Задание 65.2. По наклонной плоскости длиной I = 80 см поднимают равномерно брусок массой 102 г. При этом измеряют силу F, приложенную к бруску вдоль наклонной плоскости, и меняют высоту h наклонной плоскости. Полученные результаты измерений занесены в таблицу.
Задание 65.3. Допишите текст.
Задание 66.1. Заполните пропуски в тексте.
Задание 66.2. Выразите значения энергии в указанных единицах.
Зада?