Полезная работа идеального газа за цикл
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа 
численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу 
, абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл 
была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
|
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
| (15.1) |
где 
— работа, совершаемая газом в течение цикла, 
— количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты 
(эта величина по своему смыслу положительна), то для работы газа справедливо соотношение 
. Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя
| (15.2) |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой 
в качестве нагревателя, и некоторое другое тело с температурой 
( 
) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя 
и холодильника 
) и двух адиабат (см. рисунок).
|
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя 
) и 3-4 (при температуре холодильника 
), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
| (15.3) |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (задача 15.1.2), то изменение внутренней энергии газа в этом процессе равно нулю (ответ 2).
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что 
(ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна 
(ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу 
(ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому 
(ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу (задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя 
и отданного холодильнику 
: 
. Поэтому КПД цикла есть
|
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15.1.9
|
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна 
, температура холодильника 
(задача 15.1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
|
Отсюда находим 
. Поэтому для КПД нового цикла Карно получаем
|
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя 
в задаче 15.2.2
|
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15.2.3
|
где 
— количество теплоты, полученное от нагревателя, 
— количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
|
где 
— работа газа, 
— количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу 
(задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно 
( 
— количество теплоты, отданное холодильнику), и работа 
составляет 20 % от этой величины, то для работы справедливо соотношение 
= 0,2 ( + 100). Отсюда находим 
= 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике 
. Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике 
проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл 
к количеству теплоты 
, полученному от нагревателя 
. Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 
вдвое меньше коэффициента полезного действия процесса 1-2-3-1 
(ответ 1).
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
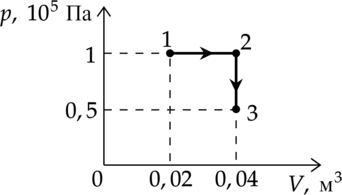
Работа газа – площадь под графиком: [A=p_1cdot(V_2-V_1)=10^5text{ Па}cdot(0,04text{ м$^3$}-0,02text{ м$^3$})=2000text{ Дж}=2text{ кДж}]
Ответ: 2
Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=300text{ Дж}-100text{ Дж}=200 text{ Дж}]
Ответ: 200
Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=100text{ Дж}-(-100text{ Дж})=200 text{ Дж}]
Ответ: 200
На pV-диаграмме изображены циклические процессы, совершаемые идеальным газом в количестве 1 моль. Определите отношение работы газа в циклическом процессе ВСDВ к работе газа в циклическом процессе АВDFА.
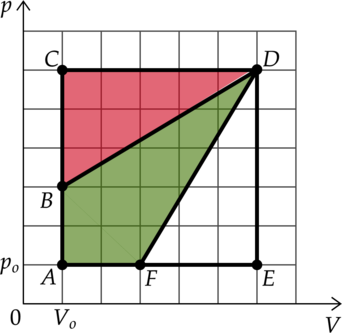[frac{A_{BCDB}}{A_{ABDFA}}=frac{0,5cdot3cdot5}{5cdot5-2cdot0,5cdot3cdot5}=0,75]
Ответ: 0,75
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразите в кДж.
Первое начало термодинамики: [Q=Delta U+A_{text{г}}] [A_{text{г}}=Q-Delta U]
Подставим исходные значения: [A_{text{г}}=Q-Delta U=-10text{ кДж}-30text{ кДж}=-40 text{ кДж}] [A_{text{вн.с.}}=-A_{text{г}}=40 text{ кДж}]
Ответ: 40
В цилиндр с подвижным поршнем накачали (nu = 2) моля идеального одноатомного газа при температуре (t_1 = 50) (^{circ}C). Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры (t_2 = 20) (^{circ}C). Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна. Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ дайте в кДж округлите до целых.
В первом процессе газ расширяется при постоянном давлении. От объема 0 до (V_1) [A_{1-2}=p(V_1-0)=pV_1=nu RT_1]
Без теплообмена с окружающей средой означает, что процесс – адиабатический [Q=Delta U+A_{2-3}=0] [A_{2-3}=-Delta U_{2-3}]
Подставим исходные значения: [A=A_{1-2}+A_{2-3}=nu RT_1+frac{3}{2}nu R(T_1-T_2)=] [=2text{ моль}cdot8,3text{ Дж/моль·К}cdot323text{ K}+frac{3}{2}cdot2text{ моль}cdot8,3text{ Дж/моль·К}cdot30{ K}approx 6000text{ Дж}approx 6 text{ кДж}]
Ответ: 6
С массой (m = 80) г идеального газа, молярная масса которого (M = 28) г/моль, совершается циклический процесс, изображенный на рисунке. Какую работу (A) совершает такой двигатель за один цикл, если (T_1 = 300) К, (T_2 = 1000) К, а при нагревании на участке 4 – 1 давление газа увеличивается в 2 раза? Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ округлите до целых.
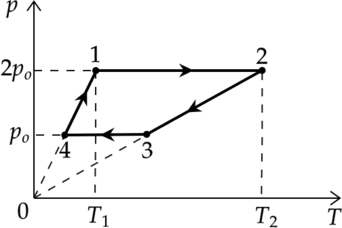
1-2 и 3-4 – изобарные процессы
2-3 и 4-1 – изохорные процессы
Перерисуем график в координатах (pV)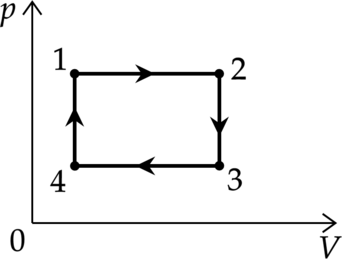 
Так как 2-3 и 4-1 – изохорные процессы, то (Tsim p). Давление увеличивается в 2 раза, то температура увеличивается в 2 раза. Следовательно: [T_4=frac{T_1}{2}=150 text{ К}] [T_3=frac{T_2}{2}=500 text{ К}]
Работа газа цикл – площадь внутри графика в координатах (pV) [A=(p_1-p_4)cdot(V_2-V_1)=(2p_4-p_4)cdot(V_2-V_1)=p_4cdot(V_2-V_1)=p_4V_2-p_4V_1]
Подставим исходные значения,переведя все единицы в систему СИ: [A=p_4V_2-p_4V_1=nu RT_3-nu RT_4=nu R(T_3-T_4)=frac{m}{M}R(T_3-T_4)=] [=frac{0,08text{ кг}}{0,028text{ кг/моль}}cdot8,31text{ Дж/(моль$cdot$ К)}cdot(500 text{ К} — 150 text{ К})= 8310 text{ Дж}]
Ответ: 8310
Источник
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1; объем газа в конечном состоянии V 2). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
Рис. 6.1
Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:
A = p?V, или A = νR?T,
где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V 2 − V 1; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T 2 − T 1; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе (V = const) не совершается:
A = 0.
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.
Рис. 6.2
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
· положительной (прямой цикл);
· отрицательной (обратный цикл).
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м3; 75,0 кПа), (0,0750 м3; 125 кПа), (0,0750 м3; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:
A = p?V = p(V 2 − V 1),
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
p = p 1 + p 2,
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
· парциальное давление водорода
p1=m1M1RT1V1,
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
· парциальное давление гелия
p2=m2M2RT1V1,
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
A=(p1+p2)(V2−V1)=(m1M1RT1V1+m2M2RT1V1)(V2−V1).
Преобразование данного уравнения к виду
A=(m1M1+m2M2)RT1V1(V2−V1)=(m1M1+m2M2)RT1(V2V1−1)
позволяет выразить искомое отношение объемов
V2V1=A(m1M1+m2M2)RT1+1.
Вычислим:
V2V1=46⋅103(2,0⋅10−32,0⋅10−3+4,2⋅10−34,0⋅10−3)⋅8,31⋅300+1=10.
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
Источник