Полезные формулы для егэ по математике

Формулы для профильного ЕГЭ-2020 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c«a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)^2alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` | `kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Источник
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
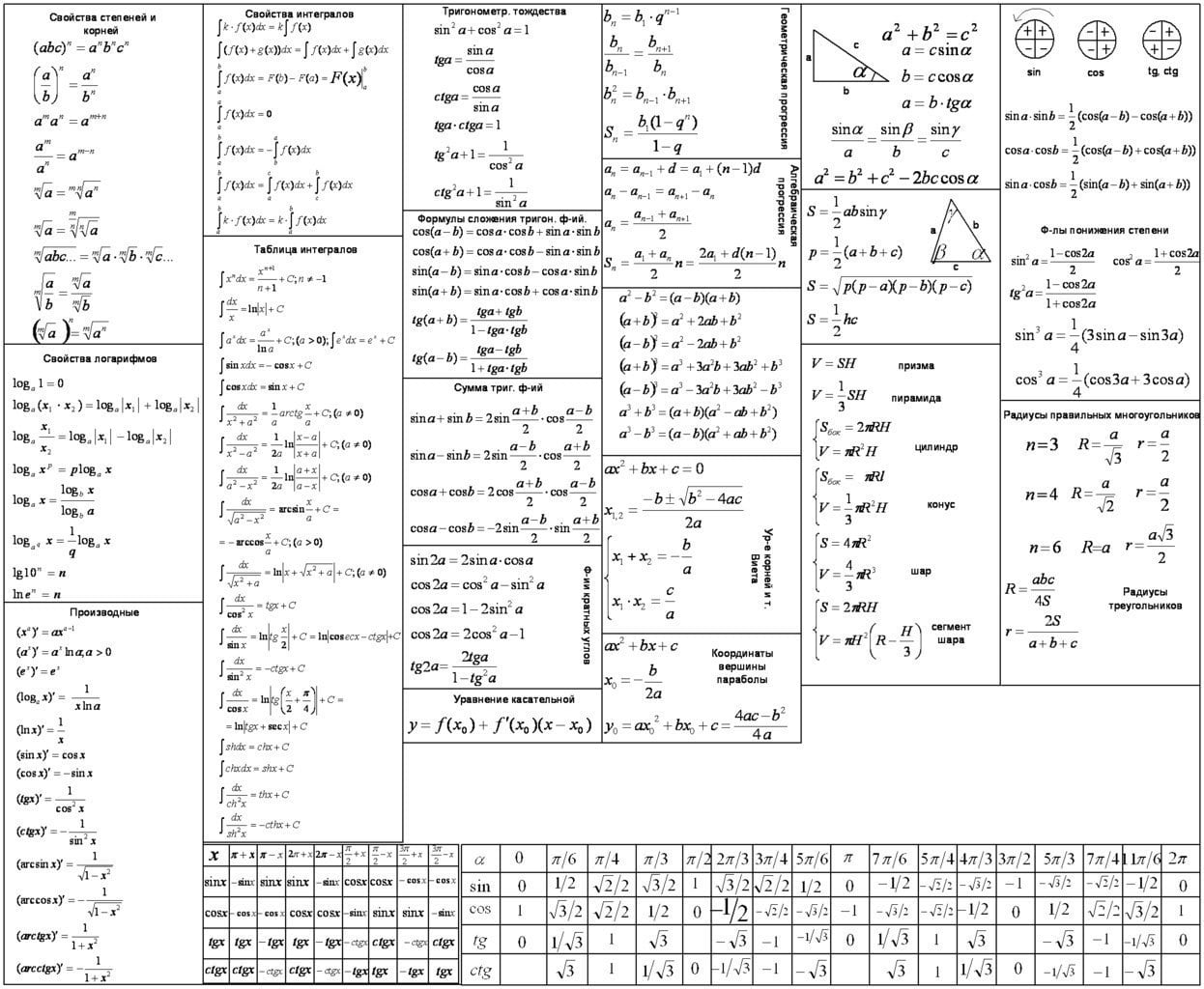
Формулы сокращенного умножения
(а+b)2 = a2 + 2ab + b2
(а-b)2 = a2 – 2ab + b2
a2 – b2 = (a-b)(a+b)
a3 – b3 = (a-b)( a2 + ab + b2)
a3 + b3 = (a+b)( a2 – ab + b2)
(a + b)3 = a3 + 3a2b+ 3ab2+ b3
(a – b)3 = a3 – 3a2b+ 3ab2- b3
Свойства степеней
a0 = 1 (a≠0)
am/n = (a≥0, n ε N, m ε N)
a- r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
(a m) n = a mn
(ab) n = a n b n
(a/b) n = a n/ b n
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
для f(x)
Функция f(x) = Первообразная F(x)
k = kx + C
xn = xn+1/n+1 + C
1/x = ln |x| + C
ex = ex + C
ax = ax/ ln a + C
1/√x = 2√x + C
cos x = sin x + C
1/ sin2 x = – ctg x + C
1/ cos2 x = tg x + C
sin x = – cos x + C
1/ x2 = – 1/x
Геометрическая прогрессия
bn+1 = bn · q, где n ε N
q – знаменатель прогрессии
bn = b1 · qn – 1 – n-ый член прогрессии
Сумма n-ыхчленов
Sn = (b n q – b 1 )/q-1
Sn = b 1 (q n – 1 )/q-1
Модуль
|a| = a, если a≥0
-a, если a<0
Формулы cos и sin
sin (-x) = -sin x
cos (-x) = cos x
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призмаSБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a3 ; P = 6 a2
5. Пирамида, правильная и неправ.
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr2h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr2h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 0, x = πn
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 -+ tg x ·tg y
ctg (x ±y) = tg x -+ tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x-+y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x-+y/2)
1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2
1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2
6. Трапеция
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
7. Квадрат
а – сторона, d – диагональ S = a2 = d2/2
8. Ромб
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a2
10. Круг
S = (L/2) r = πr2 = πd2/4
11. Сектор
S = (πr2/360) α
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(k(f(x))’ = kf ’ (x)
(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)
(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)
(xn)’ = nx n-1
(tg x)’ = 1/ cos2 x
(ctg x)’ = – 1/ sin2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
y = f ’(a) (x-a) + f(a)
Площадь S фигуры, ограниченной прямыми x=a, x=b
S = ∫( f(x) – g(x)) dx
Формула Ньютона-Лебница
∫ab f(x) dx = F(b) – F (a)
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | -√2/2 | 1 | |
| sin | √2/2 | 1 | √2/2 | |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | √2/2 | 1 | |
| sin | -√2/2 | -1 | -√2/2 | |
| t | π/6 | π/4 | π/3 | |
| tg | √3/3 | 1 | √3 | |
| ctg | — | √3 | 1 | √3/3 |
sin x = b x = (-1)n arcsin b + πn
https://5-ege.ru/shpargalki-po-matematike/
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теоремасинусов: a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов: с2=a2+b2-2ab cos y
Неопределенные интегралы
∫ dx = x + C
∫ xn dx = (xn+1/n+1) + C
∫ dx/x2 = -1/x + C
∫ dx/√x = 2√x + C
∫ (kx+b) = 1/k F(kx + b)
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin2 x = -ctg + C
∫ dx/cos2 x = tg + C
∫ x r dx = x r+1/r+1 + C
Логарифмы
1. loga a = 1
2. loga 1 = 0
3. loga (bn) = n loga b
4. log An b = 1/n loga b
5. loga b = log c b/ log c a
6. loga b = 1/ log b a
| Градус | 30 | 45 | 60 | |
| sin | 1/2 | √2/2 | √3/2 | |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | √3/3 | 1 | √3 | |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | |
| -1/2 | -√2/2 | -√3/2 | -1 | |
| — | -√3 | -1 | √3/3 | |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x
tg 2x = 2 tg x/ 1 – tg2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin3 x
cos 3x = 4 cos3 x – 3 cos x
tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
c’ = 0 ()’ = 1/ 2
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x2) ( ln x)’ = 1/x
(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b2 – a2/4
3. Равносторонний треугольник
S = (a2/4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a2b sin C =
a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
5. Параллелограмм
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
tg(-x) = – tg x
ctg(-x) = – ctg x
tg (x + πk) = tg x
ctg (x + πk) = ctg x
tg (x ± π) = ± tg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin2 x + cos2 x =1
tg x · ctg x = 1
1 + tg2 x = 1/ cos2 x
1 + ctg2 x = 1/ sin2 x
tg2 (x/2) = 1 – cos x/ 1 + cos x
cos2 (x/2) = 1 + cos x/ 2
sin2 (x/2) = 1 – cos x/ 2
11. Шар: V=4/3 πR3 = 1/6 πD3
P = 4 πR2 = πD2
12. Шаровой сегмент
V = πh2 (R-1/3h) = πh/6(h2 + 3r2)
SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)
13. Шаровой слой
V = 1/6 πh3 + 1/2 π(r2 + h2)· h;
SБОК = 2 π·R·h
14. Шаровой сектор:
V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
(a≥0, b≥0)
(a≥0)
ax2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b2-4ac)
Если D>0, то x1,2 = -b± /2a
Теорема Виета
x1 + x2 = -b/a
x1 · x2 = c/a
Арифметическая прогрессия
a n+1 = an + d, где n – натуральное число
d – разность прогрессии;
a n= a 1 + (n – 1)·d – формула n-го члена
Сумма n членов
Sn = ((a 1 + a n )/2) · n
Sn = ((2a 1 + (n-1)d)/2) · n
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
r = a/ 2 tg 180/n
Окружность
L = 2 πR S = πR2
Площадь конуса
S БОК = πRL
S КОН= πR(L+R)
Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем:
Источник
Формулы по базовой математике для ЕГЭ
Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:
- таблица квадратных чисел от 0 до 99;
- свойства арифметического квадратного корня;
- формулы сокращенного умножения;
- корни квадратного уравнения;
- свойства степени и логарифма;
- теорема Пифагора;
- формула расчета длины окружности и площади круга;
- расчет средней линии треугольника и трапеции;
- радиус вписанной и описанной окружности правильного треугольника;
- формулы расчета площади планиметрических фигур;
- вычисление поверхностей и объемов тел;
- основные тригонометрические функции и тождества;
- график линейной функции;
- геометрический смысл производной.
Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.
Основные формулы для профильного ЕГЭ
Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.

Естественно, чтобы сдать профильную математику, для ЕГЭ потребуется запомнить намного больше формул. Выяснить, на какие темы нужно обратить внимание, можно по тому же алгоритму, что и для базы (из КЭС или, решая тренировочные задания).
Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:
- правила сокращенного умножения;
- арифметическая и геометрическая прогрессии;
- основы вероятностной теории;
- свойства степеней и логарифмов;
- азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
- производная (правила дифференцирования, элементарнее функции и уравнение касательной);
- первообразная;
- двухмерная планиметрия;
- правила нахождения площадей геометрических фигур;
- трехмерная стереометрия.
Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:
- ЕГЭ по математике – формулы для алгебры и начал анализа
- Формулы ЕГЭ – математика, раздел геометрия
Материалы для скачивания – в формате pdf.
Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.
Математика
+27
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по математике
Русский язык
+30
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по русскому языку
Обществознание
+25
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по обществознанию
Физика
+31
балл
к ЕГЭ
Курсы подготовки к ЕГЭ по физике
Английский язык
+24
балла
к ЕГЭ
Курсы подготовки к ЕГЭ по английскому языку
Биология
+29
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по биологии
Источник
Анна Малкова
Что проще запомнить с первого раза и пересказать другу – сюжет интересного фильма или большую таблицу с формулами по геометрии?
Мы хорошо запоминаем сюжеты и истории. А однообразная и скучная информация быстро вылетает из головы.
Можно запоминать формулы «как буковки». Долго, трудно и напряженно. Результат – вы сами знаете, какой.
А можно придумать историю. Понять, почему формула именно такая. Как она получилась. На что она похожа.
Например, формулы для площадей геометрических фигур. Они есть в нашем ЕГЭ-Справочнике
Площадь прямоугольника равна произведению его сторон:

Чем больше стороны, тем больше площадь. Проверяйте, чтобы площадь была выражена в квадратных единицах.
Отрежем от нашего прямоугольника треугольник. И переставим этот треугольник, как на рисунке, получим параллелограмм.
Площадь параллелограмма:

Поделим параллелограмм пополам. Получим два равных треугольника и формулу для площади треугольника:

Теперь трапеция. Поделим ее на два треугольника с основаниями и .
Площадь трапеции

В формулы для длины окружности и площади круга входит число .
Длина окружности
.
Число – это отношение длины окружности к ее диаметру.
.
Число известно с глубокой древности. С давних времен – с доисторических – люди плели круглые корзины и лепили из глины круглые тарелки и миски. Во всяком случае, старались сделать их круглыми.
Нарисуйте древнего человека, который плетет корзинку. Он смотрит на небо и видит на нем круглое солнце. Он старается, чтобы его корзина получилась круглой, как солнце. Измерив диаметр своего изделия, наш первобытный труженик осознает, что диаметр укладывается на окружности корзины три раза, и еще немного остается! Причем это справедливо и для маленькой корзины, и для большой. Удивительное открытие!
Во сколько же раз длина окружности больше, чем ее диаметр? В раз.

площадь выражается в квадратных единицах, значит, в формуле должен быть квадрат радиуса.
Площадь круга
Формулу для площади сектора запомнить легко. Кусочки, на которые вы нарезаете круглую пиццу, – это секторы.

Вспомним, что 1 градус – это часть полного круга. Тогда площадь сектора в 1 градус равна части полного круга. А площадь сектора в градусов равна части полного круга.
Точно так же для длины дуги:
Есть отличная «запоминалка», и ее все знают.
Биссектриса – это крыса, которая бегает по углам и делит угол пополам.
Нарисуем угол, который крыса делит пополам, и эта крыса тащит за собой (на хвосте) круглый сыр. Центр окружности, вписанной в угол, лежит на биссектрисе угла.

Прогоним крысу, оставим вписанную в угол окружность. Отрезки касательных, проведенных из одной точки к окружности, равны.

А поскольку прямоугольные треугольники АОВ и СОВ на рисунке равны – значит, равны расстояния от точки до точек и . Биссектриса угла треугольника – это множество точек, равноудаленных от сторон угла.
Впишем в треугольник окружность. Окружность касается всех сторон треугольника – значит, ее центр одинаково удален от сторон АВ, ВС и АС. Центр окружности, вписанной в треугольник, – это точка пересечения его биссектрис.

А где же находится центр окружности, описанной вокруг треугольника? Очевидно, что расстояние от этой точки до всех вершин треугольника одинаково и равно радиусу описанной окружности.
Где находятся точки, равноудаленные от концов отрезка, вы знаете. На серединном перпендикуляре к отрезку.

Вот и нарисуем три серединных перпендикуляра к сторонам треугольника. А в точке, где все они пересекаются, уселась киса, чтобы быть на одинаковом расстоянии от вершин треугольника. А что делает киса? – правильно, писает! Хочет до всех вершин треугольника достать. И получается окружность, описанная вокруг треугольника.

Чтобы легко запоминать формулы, придумывайте истории. Глупые, смешные, даже неприличные. И картинки к ним рисуйте!
Теперь стереометрия. Будем искать логические связи. Ассоциации. Придумываеть себе «запоминалки».
Посмотрим на таблицу с формулами для объемов и площадей поверхности многогранников и тел вращения.
С призмой и цилиндром все просто – их объем равен произведению площади основания на высоту.
Чем больше площадь основания, тем больше объем.
Чем больше высота, тем больше объем.
Объем призмы

Объем цилиндра

С объемами пирамиды и конуса тоже просто: умножаем на площадь основания и на высоту. Как вы думаете, почему у пирамиды и у конуса похожие формулы для объема?
Объем пирамиды
Объем конуса

Площадь боковой поверхности многогранника равна сумме площадей всех его граней. Сложные формулы здесь не нужны.
Теперь цилиндр. В его основаниях – два круга. Как запомнить, чему равна площадь поверхности цилиндра? Развернем боковую поверхность цилиндра и получим прямоугольник, одна сторона которого равна , а другая равна .

Площадь боковой поверхности цилиндра
Как запомнить формулу для площади боковой поверхности конуса?*
Нарисуем ракушку в форме конуса. Вот у него какая красивая боковая поверхность.

А в ракушке что бывает? – жемчужинка! По-английски жемчужина: pearl. Вот и запомним формулу для площади боковой поверхности конуса:
Остались объем шара и площадь поверхности сферы .
Что же, две формулы можно и просто выучить.
Хорошо, а как выучить формулы тригонометрии?
Есть отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!
И конечно, чем больше решаете задач, тем лучше запоминаются формулы.
*Лайфхак преподавателя ЕГЭ-Студии А.В. Фомичевой
Источник
Формулы сокращенного умножения
(а+b)2 = a2 + 2ab + b2
(а-b)2 = a2 – 2ab + b2
a2 – b2 = (a-b)(a+b)
a3 – b3 = (a-b)( a2 + ab + b2)
a3 + b3 = (a+b)( a2 – ab + b2)
(a + b)3 = a3 + 3a2b+ 3ab2+ b3
(a – b)3 = a3 – 3a2b+ 3ab2- b3
Свойства степеней
a0 = 1 (a≠0)
am/n = (a≥0, n ε N, m ε N)
a- r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
(a m) n = a mn
(ab) n = a n b n
(a/b) n = a n/ b n
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
для f(x)
Функция f(x) = Первообразная F(x)
k = kx + C
xn = xn+1/n+1 + C
1/x = ln |x| + C
ex = ex + C
ax = ax/ ln a + C
1/√x = 2√x + C
cos x = sin x + C
1/ sin2 x = – ctg x + C
1/ cos2 x = tg x + C
sin x = – cos x + C
1/ x2 = – 1/x
Геометрическая прогрессия
b n+1 = bn · q, где n ε N
q – знаменатель прогрессии
b n = b1 · q n – 1 – n-ый член прогрессии
Сумма n-ых членов
S n = (b n q – b 1 )/q-1
S n = b 1 (q n – 1 )/q-1
Модуль
|a| = a, если a≥0
-a, если a<0
Формулы cos и sin
sin (-x) = -sin x
cos (-x) = cos x
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призма SБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a3 ; P = 6 a2
5. Пирамида, правильная и неправ.
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr2h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr2h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 0, x = πn
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 -+ tg x ·tg y
ctg (x ±y) = tg x -+ tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x-+y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x-+y/2)
1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2
1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2
6. Трапеция
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
7. Квадрат
а – сторона, d – диагональ S = a2 = d2/2
8. Ромб
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a2
10. Круг
S = (L/2) r = πr2 = πd2/4
11. Сектор
S = (πr2/360) α
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(k(f(x))’ = kf ’ (x)
(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)
(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)
(xn)’ = nx n-1
(tg x)’ = 1/ cos2 x
(ctg x)’ = – 1/ sin2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
y = f ’(a) (x-a) + f(a)
Площадь S фигуры, ограниченной прямыми x=a, x=b
S = ∫( f(x) – g(x)) dx
Формула Ньютона-Лебница
∫ab f(x) dx = F(b) – F (a)
t
π/4
π/2
3π/4
π
cos
√2/2
0
-√2/2
1
sin
√2/2
1
√2/2
0
t
5π/4
3π/2
7π/4
2π
cos
-√2/2
0
√2/2
1
sin
-√2/2
-1
-√2/2
0
t
π/6
π/4
π/3
tg
0
√3/3
1
√3
ctg
—
√3
1
√3/3
in x = b x = (-1)n arcsin b + πn
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теорема синусов: a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов: с2=a2+b2-2ab cos y
Неопределенные интегралы
∫ dx = x + C
∫ xn dx = (x n +1/n+1) + C
∫ dx/x2 = -1/x + C
∫ dx/√x = 2√x + C
∫ (kx+b) = 1/k F(kx + b)
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin2 x = -ctg + C
∫ dx/cos2 x = tg + C
∫ x r dx = x r+1/r+1 + C
Логарифмы
1. loga a = 1
2. loga 1 = 0
3. loga (bn) = n loga b
4. log An b = 1/n loga b
5. loga b = log c b/ log c a
6. loga b = 1/ log b a
Градус
30
45
60
sin
0
1/2
√2/2
√3/2
cos
1
√3/2
√2/2
1/2
tg
0
√3/3
1
√3
t
π/6
π/3
2π/3
5π/6
cos
√3/2
1/2
-1/2
-√3/2
sin
1/2
√3/2
√3/2
1/2
90
120
135
150
180
1
√3/2
√2/2
1/2
0
0
-1/2
-√2/2
-√3/2
-1
—
-√3
-1
√3/3
0
t
7π/6
4π/3
5π/3
11π/6
cos
-√3/2
-1/2
1/2
√3/2
sin
-1/2
-√3/2
-√3/2
-1/2
Формулы двойного аргумента
cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x
tg 2x = 2 tg x/ 1 – tg2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin3 x
cos 3x = 4 cos3 x – 3 cos x
tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
c’ = 0 ()’ = 1/ 2
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x2) ( ln x)’ = 1/x
(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b2 – a2/4
3. Равносторонний треугольник
S = (a2/4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a2b sin C =
a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
5. Параллелограмм
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
tg(-x) = – tg x
ctg(-x) = – ctg x
tg (x + πk) = tg x
ctg (x + πk) = ctg x
tg (x ± π) = ± tg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin2 x + cos2 x =1
tg x · ctg x = 1
1 + tg2 x = 1/ cos2 x
1 + ctg2 x = 1/ sin2 x
tg2 (x/2) = 1 – cos x/ 1 + cos x
cos2 (x/2) = 1 + cos x/ 2
sin2 (x/2) = 1 – cos x/ 2
11. Шар: V=4/3 πR3 = 1/6 πD3
P = 4 πR2 = πD2
12. Шаровой сегмент
V = πh2 (R-1/3h) = πh/6(h2 + 3r2)
SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)
13. Шаровой слой
V = 1/6 πh3 + 1/2 π(r2 + h2)· h;
SБОК = 2 π·R·h
14. Шаровой сектор:
V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
(a≥0, b≥0)
(a≥0)
ax2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b2-4ac)
Если D>0, то x1,2 = -b± /2a
Теорема Виета
x1 + x2 = -b/a
x1 · x2 = c/a
Арифметическая прогрессия
a n+1 = a n + d, где n – натуральное число
d – разность прогрессии;
a n = a 1 + (n – 1)·d – формула n-го члена
Сумма n членов
S n = ((a 1 + a n )/2) · n
S n = ((2a 1 + (n-1)d)/2) · n
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
r = a/ 2 tg 180/n
Окружность
L = 2 πR S = πR2
Площадь конуса
S БОК = πRL
S КОН = πR(L+R)
Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Источник

