Полезные формулы по геометрии для егэ
Формулы для профильного ЕГЭ-2020 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c«a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)^2alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` | `kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
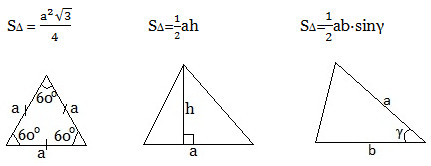
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Источник
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны и сантиметров соответственно. Постройте треугольник с помощью циркуля и линейки.
б) В треугольнике угол равен градусов, сторона равна двум, равна . Постройте треугольник .
в) В треугольнике сторона равна , угол равен , угол равен . Постройте треугольник .
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) три биссектрисы.
в) три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса
— для острого угла прямоугольного треугольника
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и .
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте
а) окружность, вписанную в данный треугольник
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Источник

СПРАВОЧНЫЙ МАТЕРИАЛ ПО ГЕОМЕТРИИ ДЛЯ 7-11 КЛАССОВ.

Уважаемые родители! Если Вы ищите репетитора по математике для Вашего ребёнка, то это объявление для Вас. Предлагаю скайп-репетиторство: подготовка к ОГЭ, ЕГЭ, ликвидация пробелов в знаниях. Ваши выгоды очевидны:
1) Ваш ребенок находится дома, и Вы можете быть за него спокойны;
2) Занятия проходят в удобное для ребенка время, и Вы даже можете присутствовать на этих занятиях. Объясняю я просто и доступно на всем привычной школьной доске.
3) Другие важные преимущества скайп-занятий додумаете сами!
Напишите мне по адресу: a@tayak.ru или сразу добавляйтесь ко мне в скайп, и мы обо всём договоримся. Цены доступные.
P.S. Возможны занятия в группах по 2-4 учащихся.
С уважением Татьяна Яковлевна Андрющенко.
 Друзья! Весь справочный материал (и по алгебре, и по геометрии) в виде сборника 431 формул и правил вы можете получить здесь. Распечатаете, и получится удобная книжечка! Инструкцию по распечатке смотрите здесь.
Друзья! Весь справочный материал (и по алгебре, и по геометрии) в виде сборника 431 формул и правил вы можете получить здесь. Распечатаете, и получится удобная книжечка! Инструкцию по распечатке смотрите здесь.
P.S. Друзья, конечно, это бесплатно!
Дорогие друзья! Готовитесь к ОГЭ или ЕГЭ?
Вам в помощь «Справочник по геометрии 7-9». Подробнее здесь.
Определение параллелограмма.
 Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны: AB||CD, AD||DC.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны: AB||CD, AD||DC.
Cвойства параллелограмма.
 Противоположные стороны параллелограмма равны: AB=CD, AD=DC.
Противоположные стороны параллелограмма равны: AB=CD, AD=DC.
 Противоположные углы параллелограмма равны:
Противоположные углы параллелограмма равны:
∠A=∠C, ∠B=∠D.
Сумма углов параллелограмма, прилежащих к одной его стороне составляет 180°.Например, ∠A+∠B=180°.
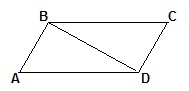
Любая диагональ параллелограмма делит его на два равных треугольника. Δ ABD=Δ BCD.
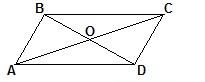
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD. Пусть АС=d1 и BD=d2 , ∠COD=α. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
(d1)2+(d2)2=2 (a2+b2).
Признаки параллелограмма.
- Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.
- Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
- Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Площадь параллелограмма.
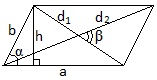 1) S=ah;
1) S=ah;
2) S=ab∙sinα;
3) S=(½) d1∙d2∙sinβ.
Прямоугольник.
 Прямоугольник — это параллелограмм, у которого все углы прямые. ABCD — прямоугольник. Прямоугольник обладает всеми свойствами параллелограмма.
Прямоугольник — это параллелограмм, у которого все углы прямые. ABCD — прямоугольник. Прямоугольник обладает всеми свойствами параллелограмма.
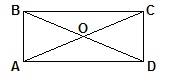 Диагонали прямоугольника равны.
Диагонали прямоугольника равны.
AC=BD. Пусть АС=d1 и BD=d2 , ∠COD=α.
d1=d2 – диагонали прямоугольника равны. α – угол между диагоналями.
Квадрат диагонали прямоугольника равен сумме квадратов сторон прямоугольника:
(d1)2=(d2)2=a2+b2.
Площадь прямоугольника можно найти по формулам:
1) S=ab; 2) S=(½)· d²∙sinα; (d- диагональ прямоугольника).
Около любого прямоугольника можно описать окружность, центр которой – точка пересечения диагоналей; диагонали являются диаметрами окружности.
Ромб.
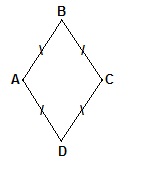 Ромб — это параллелограмм, у которого все стороны равны.
Ромб — это параллелограмм, у которого все стороны равны.
ABCD — ромб.
Ромб обладает всеми свойствами параллелограмма.
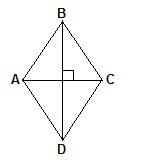
Диагонали ромба взаимно перпендикулярны.
AC | BD.
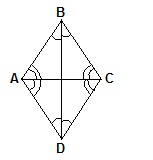
Диагонали ромба являются биссектрисами его углов.
Площадь ромба.
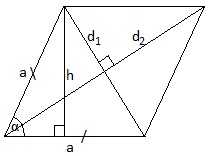 1) S=ah;
1) S=ah;
2) S=a2∙sinα;
3) S=(½) d1∙d2;
4) S= P∙r, где P – периметр ромба, r – радиус вписанной окружности.
Квадрат.
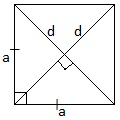 Все стороны квадрата равны, диагонали квадрата равны и пересекаются под прямым углом.
Все стороны квадрата равны, диагонали квадрата равны и пересекаются под прямым углом.
Диагональ квадрата d=a√2.
Площадь квадрата. 1) S=a2; 2) S=(½) d2.
Трапеция.
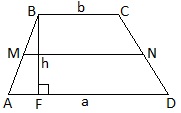 Основания трапеции AD||BC, MN-средняя линия
Основания трапеции AD||BC, MN-средняя линия
MN=(AD+BC)/2.
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
S=(AD+BC)∙BF/2 или S=(a+b)∙h/2.
В равнобедренной (равнобокой) трапеции длины боковых сторон равны; углы при основании равны.
Площадь любого четырехугольника.
- Площадь любого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
S=(½) d1∙d2∙sinβ.
- Площадь любого четырехугольника равна половине произведения его периметра на радиус вписанной окружности:
S=(½) P∙r.
Вписанные и описанные четырехугольники.
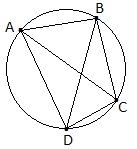 В выпуклом четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).
В выпуклом четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).
AC∙BD=AB∙DC+AD∙BC.
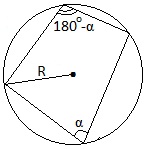
Если суммы противолежащих углов четырехугольника равны по 180°, то около четырехугольника можно описать окружность. Обратное утверждение также верно.
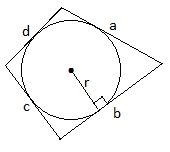
Если суммы противолежащих сторон четырехугольника равны (a+c=b+d), то в этот четырехугольник можно вписать окружность. Обратное утверждение также верно.
Окружность, круг.
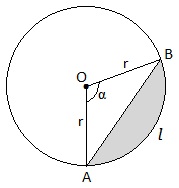 1) Длина окружности С=2πr;
1) Длина окружности С=2πr;
2) Площадь круга S=πr2;
3) Длина дуги АВ:
![]()
4) Площадь сектора АОВ:
![]()
5) Площадь сегмента (выделенная область):
![]()
(«-» берут, если α<180°; «+» берут, если α>180°), ∠AOB=α – центральный угол. Дуга l видна из центра O под углом α.
Теорема Пифагора.
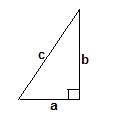
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b².
Площадь прямоугольного треугольника.
SΔ=(½) a∙b, где a и b — катеты или SΔ=(½) c∙h, где с — гипотенуза, h –высота, проведенная к гипотенузе.
Радиус вписанной в прямоугольный треугольник окружности.
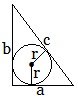 2r=a+b-c
2r=a+b-c
Пропорциональные отрезки в прямоугольном треугольнике.
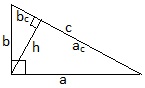 Высота, проведенная из вершины прямого угла к гипотенузе есть средняя пропорциональная величина между проекциями катетов на гипотенузу: h2=ac∙bc;
Высота, проведенная из вершины прямого угла к гипотенузе есть средняя пропорциональная величина между проекциями катетов на гипотенузу: h2=ac∙bc;
а каждый катет есть средняя пропорциональная величина между всей гипотенузой и проекцией данного катета на гипотенузу: a2=c∙ac и b2=c∙bc (произведение средних членов пропорции равно произведению ее крайних членов: h, a, b — средние члены соответствующих пропорций).
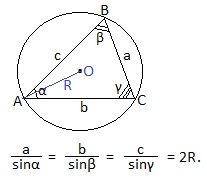
Теорема синусов.
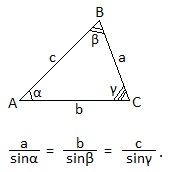
В любом треугольнике стороны пропорциональны синусам противолежащих углов.
Следствие из теоремы синусов.
 Каждое из отношений стороны к синусу противолежащего угла равно 2R, где R — радиус окружности, описанной около треугольника.
Каждое из отношений стороны к синусу противолежащего угла равно 2R, где R — радиус окружности, описанной около треугольника.
Теорема косинусов.
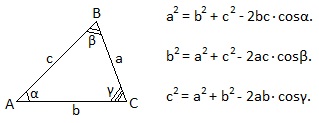
Квадрат любой стороны треугольника равен сумме квадратов двух других ее сторон без удвоенного произведения этих сторон на косинус угла между ними.
Свойства равнобедренного треугольника.
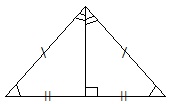 В равнобедренном треугольнике (длины боковых сторон равны) высота, проведенная к основанию, является медианой и биссектрисой. Углы при основании равнобедренного треугольника равны.
В равнобедренном треугольнике (длины боковых сторон равны) высота, проведенная к основанию, является медианой и биссектрисой. Углы при основании равнобедренного треугольника равны.
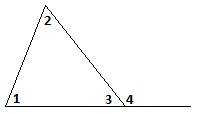 Сумма внутренних углов любого треугольника составляет 180°, т. е. ∠1+∠2+∠3=180°.
Сумма внутренних углов любого треугольника составляет 180°, т. е. ∠1+∠2+∠3=180°.
Внешний угол треугольника (∠4) равен сумме двух внутренних, не смежных с ним, т. е. ∠4=∠1+∠2.
Средняя линия треугольника соединяет середины боковых сторон треугольника.
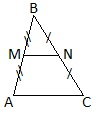 Средняя линия треугольника параллельна основанию и равна его половине: MN=AC/2.
Средняя линия треугольника параллельна основанию и равна его половине: MN=AC/2.
Площадь треугольника.
Формула Герона.
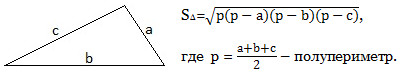
Центр тяжести треугольника.
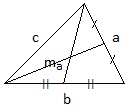 Центр тяжести треугольника — точка пересечения медиан, которая делит каждую медиану в отношении 2:1, считая от вершины.
Центр тяжести треугольника — точка пересечения медиан, которая делит каждую медиану в отношении 2:1, считая от вершины.
Длина медианы, проведенной к стороне а:
![]()
Медиана делит треугольник на два равновеликих треугольника, площадь каждого из этих двух треугольников равна половине площади данного треугольника.
Биссектриса угла треугольника.
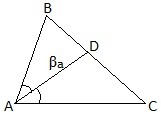 1) Биссектриса угла любого треугольника делит противоположную сторону на части, соответственно пропорциональные боковым сторонам треугольника:
1) Биссектриса угла любого треугольника делит противоположную сторону на части, соответственно пропорциональные боковым сторонам треугольника:
![]()
2) если AD=βa, то длина биссектрисы:
![]()
3) Все три биссектрисы треугольника пересекаются в одной точке.
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис углов треугольника.
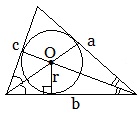 Площадь треугольника SΔ=(½) P∙r, где P=a+b+c, r-радиус вписанной окружности.
Площадь треугольника SΔ=(½) P∙r, где P=a+b+c, r-радиус вписанной окружности.
Радиус вписанной окружности можно найти по формуле:
![]()
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к 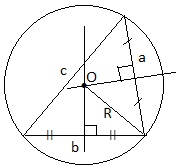 сторонам треугольника.
сторонам треугольника.
Радиус окружности, описанной около любого треугольника:
![]()
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы: R=АВ/2;
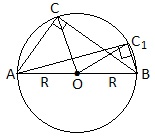 Медианы прямоугольных треугольников, проведенных к гипотенузе, равны половине гипотенузы (это радиусы описанной окружности) OC=OC1=R.
Медианы прямоугольных треугольников, проведенных к гипотенузе, равны половине гипотенузы (это радиусы описанной окружности) OC=OC1=R.
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.
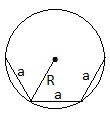 Окружность, описанная около правильного n-угольника.
Окружность, описанная около правильного n-угольника.
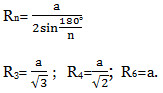
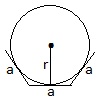 Окружность, вписанная в правильный n-угольник.
Окружность, вписанная в правильный n-угольник.
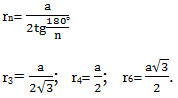
 Сумма внутренних углов любого выпуклого n-угольника равна 180°(n-2).
Сумма внутренних углов любого выпуклого n-угольника равна 180°(n-2).
Сумма внешних углов любого выпуклог0 n-угольника равна 360°.
Прямоугольный параллелепипед.
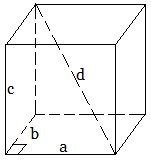 Все грани прямоугольного параллелепипеда — прямоугольники. a, b, c – линейные размеры прямоугольного параллелепипеда (длина, ширина, высота).
Все грани прямоугольного параллелепипеда — прямоугольники. a, b, c – линейные размеры прямоугольного параллелепипеда (длина, ширина, высота).
1) Диагональ прямоугольного параллелепипеда d2=a2+b2+c2;
2) Боковая поверхность Sбок.=Pосн.∙Н или Sбок.=2 (a+b)·c;
3) Полная поверхность Sполн.=2Sосн.+Sбок. или
Sполн.=2 (ab+ac+bc);
4) Объем прямоугольного параллелепипеда V=Sосн.∙Н илиV=abc.
Куб.
1) Все грани куба – квадраты со стороной а.
2) Диагональ куба d=a√3.
3) Боковая поверхность куба Sбок.=4а2;
4) Полная поверхность куба Sполн.=6а2;
5) Объем куба V=a3.
Прямой параллелепипед (в основании лежит параллелограмм или ромб, боковое ребро перпендикулярно основанию).
1) Боковая поверхность Sбок.=Pосн.∙Н.
2) Полная поверхность Sполн.=2Sосн.+Sбок.
3) Объем прямого параллелепипеда V=Sосн.∙Н.
Наклонный параллелепипед.
 В основании параллелограмм или прямоугольник или ромб или квадрат, а боковые ребра НЕ перпендикулярны плоскости основания.
В основании параллелограмм или прямоугольник или ромб или квадрат, а боковые ребра НЕ перпендикулярны плоскости основания.
1) Объем V=Sосн.∙Н;
2) Объем V=Sсеч.∙l, гдеl— боковое ребро, Sсеч.-площадь сечения наклонного параллелепипеда, проведенного перпендикулярно боковому ребру l.
Прямая призма.
 Боковая поверхность Sбок.=Pосн.∙Н;
Боковая поверхность Sбок.=Pосн.∙Н;
Полная поверхность Sполн.=2Sосн.+Sбок.;
Объем прямой призмы V=Sосн.∙Н.
Наклонная призма.
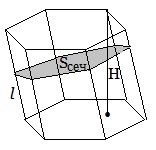 Боковая и полная поверхности, а также объем можно находить по тем же формулам, что и в случае прямой призмы. Если известна площадь сечения призмы, перпендикулярного ее боковому ребру, то объем V=Sсеч.∙l, гдеl- боковое ребро, Sсеч.-площадь сечения, перпендикулярного боковому ребру l.
Боковая и полная поверхности, а также объем можно находить по тем же формулам, что и в случае прямой призмы. Если известна площадь сечения призмы, перпендикулярного ее боковому ребру, то объем V=Sсеч.∙l, гдеl- боковое ребро, Sсеч.-площадь сечения, перпендикулярного боковому ребру l.
Пирамида.
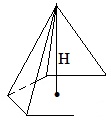 1) боковая поверхность Sбок. равна сумме площадей боковых граней пирамиды;
1) боковая поверхность Sбок. равна сумме площадей боковых граней пирамиды;
2) полная поверхность Sполн.=Sосн.+Sбок.;
3) объем V=(1/3) Sосн.∙Н.
4) У правильной пирамиды в основании лежит правильный многоугольник, а вершина пирамиды проектируется в центр этого многоугольника, т. е. в центр описанной и вписанной окружностей.
5) Апофема l –это высота боковой грани правильной пирамиды. Боковая поверхность правильной пирамиды Sбок.=(½) Pосн.∙l.
Теорема о трех перпендикулярах.
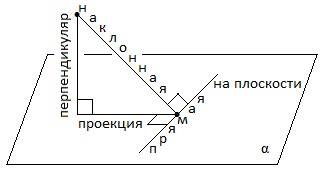 Прямая, проведенная на плоскости через основание наклонной, перпендикулярно ее проекции, перпендикулярна и самой наклонной.
Прямая, проведенная на плоскости через основание наклонной, перпендикулярно ее проекции, перпендикулярна и самой наклонной.
Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной.
Усеченная пирамида.
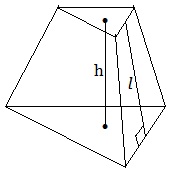 Если S и s соответственно площади оснований усеченной пирамиды, то объем любой усеченной пирамиды
Если S и s соответственно площади оснований усеченной пирамиды, то объем любой усеченной пирамиды
![]()
где h-высота усеченной пирамиды.
Боковая поверхность правильной усеченной пирамиды
![]()
где P и p соответственно периметры оснований правильной усеченной пирамиды,
l-апофема (высота боковой грани правильной усеченной пирамиды).
Цилиндр.
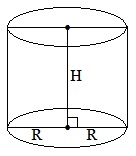 Боковая поверхность Sбок.=2πRH;
Боковая поверхность Sбок.=2πRH;
Полная поверхность Sполн.=2πRH+2πR2 или Sполн.=2πR (H+R);
Объем цилиндра V=πR2H.
Конус.
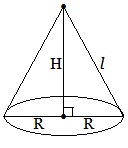 Боковая поверхность Sбок.= πRl;
Боковая поверхность Sбок.= πRl;
Полная поверхность Sполн.=πRl+πR2 или Sполн.=πR (l+R);
Объем пирамиды V=(1/3)πR2H. Здесь l – образующая, R — радиус основания, H – высота.
Шар и сфера.
Площадь сферы S=4πR2; Объем шара V=(4/3)πR3.
R – радиус сферы (шара).
Источник

