Полезные формулы по математике для огэ
Violet a 3 года назад Для у спешной сдачи математики ОГЭ нужно знать основные формулы, которые школьники изучают на уроках. Все формулы, которые пригодятся на экзамене размещены здесь, их можно скачать и распечатать. Обязательно нужно знать формулы сокращенного умножения, не помешает знание формул степеней, ещё пригодится знание формул последовательностей и прогрессий, с таблицей квадратов и степеней так же не помешает ознакомиться. Так же нужно будет знать формулы нахождения площадей различных фигур. автор вопроса выбрал этот ответ лучшим 88SkyWalker88 3 года назад Подготовка к экзамену по математике в девятом классе включает в себя повторение материала за седьмой, восьмой, девятый классы. В том числе и формулы. Помимо уже упомянутых, могут также встретиться формулы арифметической и геометрической прогрессии, определение модуля, которые ученики скорее всего знают, но повторить не мешало бы. Единый гос. экзамен по математике надо сдавать в обязательном порядке всем учащимся в 9-м классе, впрочем как дальше и в 11-м, но этот предмет не сдать если не знать базовых и нужных формул по которым можно решить задачи по геометрии и алгебре. Ниже представлю нужные формулы чтобы экзамен была возможно сдать. Перед экзаменом обязательно повторите все эти формулы. Скачать их полностью все можно с этого сайта источника. Основные — это сокращенное умножение, степени, прогрессии, геометрические и т.п. Для тех у кого гуманитарный склад ума знание формул это уже 50% успешной сдачи экзамена ОГЭ, к сожалению без него никуда. hufrcw43bkr 2 года назад Экзамены не за горами, многие ученики сейчас очень тщательно готовятся и вспоминают всю школьную программу, чтобы успешно сдать все экзамены. Такой предмет как математика один из самых сложных, но он считается обязательным, поэтому к нему готовится очень хорошо, чтобы получить хорошие отметки (баллы). Вот хорошая шпаргалка для экзамена по математике, тут и формулы степени, и формулы сокращенного умножения (как ни странно, но такое задание часто попадается на экзаменах), и логарифмы и квадратное уравнение, и производная. Из геометрии важно помнить формулы тригонометрии, это формулы косинусов и синусов, тангенсов и котангенсов. Еще больше формул можно посмотреть на этом сайте. 127771 2 года назад ОГЭ является основным государственным экзаменом для учеников девятого класса. Математика является обязательным экзаменом, поэтому ее сдают все ученики Для многих ОГЭ по математике является самым сложным экзаменов среди всех и не зря. Для экзамена необходимо не только выучить формулы, но и знать как их применять. На самом каждому необходимо составить свою шпаргалку, так кто точно эту формулу забудет, кто-то другую формулу. Ниже представлены основные формулы, которые необходимо знать успешной сдачи экзамена по математике: Также удалась найти еще один вариант формул, которые могут пригодится для подготовки к экзамену: VeneraD 2 года назад Вот и пришла пора ОГЭ, теперь все ученики пытаются наверстать все пробелы в учебе и подготовится. Чтобы сдать математику, конечно нужно знать ряд формул. В принципе все эти формулы изучают на уроках. Начинают с легкого, и в 9 классах уже конечно все сложнее. Если все темы запоминать и понимать сразу, то и на ОГЭ будет легче. Особо на шпаргалки рассчитывать не стоит, так как с каждым годом сдача ОГЭ все строже контролируется. Ниже добавлю ряд формул, есть там и степени, и квадратные корни. А еще больше формул тут. Jean Montibus-Citri 2 года назад ОГЭ — основной государственный экзамен. Его должны в обязательном порядке сдавать ученики по окончанию 9 класса, не зависимо продолжат ли они обучение в школе, или выберут профессиональное образование. ОГЭ является аналогом ЕГЭ, так что во многом задачи экзаменов перекликаются и запоминать информацию стоит всерьез и надолго. Математика и русский язык являются обязательными дисциплинами ОГЭ. Формулы, которые ученик должен знать, что бы сдать экзамен, выглядят так: Так же можно подсказать девятиклассникам вот этот сайт. Здесь представлена та же информация, но в более расширенном варианте. Те, кто запомнить все эти сочетания значков не в силах, смогут просто распечатать формулы и смастерить шпаргалку. Мурочка полосатая 2 года назад Экзамены уже совсем скоро, поэтому школьникам стоит подготовиться, особенно это касается такого предмета, как математика. Ведь это один из основных предметов, по которому обязательно сдают экзамены. Итак, начнем с формул, которые нужно знать в первую очередь, это формула сокращенного умножения, такие формулы часто встречаются в различных задачах. По геометрии нам нужно знать формулы площади различных геометрических фигур. Также необходимо помнить и знать тригонометрические функции, все что касается косинусов, синусов, тангенсов и котангенсов. Не помешает знать и и такие формулы прогрессии. Все формулы и шпаргалки смотрим на этом сайте. дольфаника 3 года назад Для успешной сдачи ОГЭ 9-классники должны знать определения и формулы по следующим темам степень и корни, преобразование многочленов, квадраты и кубы чисел, св-ва обратной пропорциональности, свойства прогрессии, свойства функции обязательно и другие. Весь список формул для ОГЭ можно посмотреть здесь. Все, что учили с первого по 9 класс по математике и геометрии, нужно знать. На основе одного правила и формулы вытекает решение задач. Незнание одной формулы ставит под угрозу сдачу всего экзамена. Поэтому перед экзаменом нужно повторить слабые места в математике, особенно проценты, в которых многие путаются. Ниже приведены все основные формулы, которые необходимо знать учащемуся общеобразовательной школы, желающему быть уверенным в своих знаниях при сдаче Основного Государственного экзамена (ОГЭ) Эти формулы — все они известны нам из курса математики пройденных девяти классов. Остается только повторить их и освежить память. Удачи на экзамене! Знаете ответ? |
Источник
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
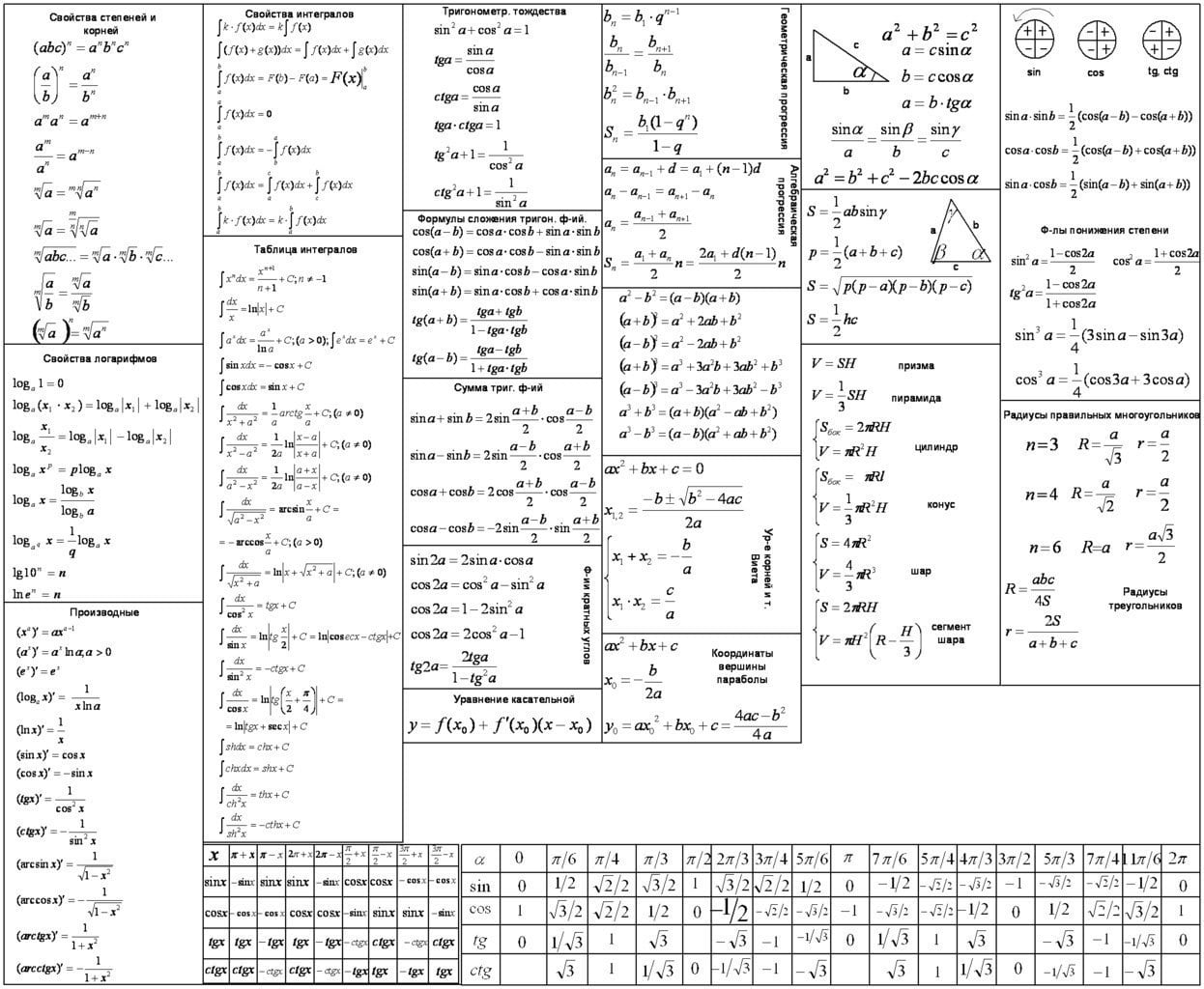
Формулы сокращенного умножения
(а+b)2 = a2 + 2ab + b2
(а-b)2 = a2 – 2ab + b2
a2 – b2 = (a-b)(a+b)
a3 – b3 = (a-b)( a2 + ab + b2)
a3 + b3 = (a+b)( a2 – ab + b2)
(a + b)3 = a3 + 3a2b+ 3ab2+ b3
(a – b)3 = a3 – 3a2b+ 3ab2- b3
Свойства степеней
a0 = 1 (a≠0)
am/n = (a≥0, n ε N, m ε N)
a- r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
(a m) n = a mn
(ab) n = a n b n
(a/b) n = a n/ b n
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
для f(x)
Функция f(x) = Первообразная F(x)
k = kx + C
xn = xn+1/n+1 + C
1/x = ln |x| + C
ex = ex + C
ax = ax/ ln a + C
1/√x = 2√x + C
cos x = sin x + C
1/ sin2 x = – ctg x + C
1/ cos2 x = tg x + C
sin x = – cos x + C
1/ x2 = – 1/x
Геометрическая прогрессия
bn+1 = bn · q, где n ε N
q – знаменатель прогрессии
bn = b1 · qn – 1 – n-ый член прогрессии
Сумма n-ыхчленов
Sn = (b n q – b 1 )/q-1
Sn = b 1 (q n – 1 )/q-1
Модуль
|a| = a, если a≥0
-a, если a<0
Формулы cos и sin
sin (-x) = -sin x
cos (-x) = cos x
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призмаSБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a3 ; P = 6 a2
5. Пирамида, правильная и неправ.
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr2h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr2h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 0, x = πn
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 -+ tg x ·tg y
ctg (x ±y) = tg x -+ tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x-+y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x-+y/2)
1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2
1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2
6. Трапеция
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
7. Квадрат
а – сторона, d – диагональ S = a2 = d2/2
8. Ромб
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a2
10. Круг
S = (L/2) r = πr2 = πd2/4
11. Сектор
S = (πr2/360) α
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(k(f(x))’ = kf ’ (x)
(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)
(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)
(xn)’ = nx n-1
(tg x)’ = 1/ cos2 x
(ctg x)’ = – 1/ sin2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
y = f ’(a) (x-a) + f(a)
Площадь S фигуры, ограниченной прямыми x=a, x=b
S = ∫( f(x) – g(x)) dx
Формула Ньютона-Лебница
∫ab f(x) dx = F(b) – F (a)
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | -√2/2 | 1 | |
| sin | √2/2 | 1 | √2/2 | |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | √2/2 | 1 | |
| sin | -√2/2 | -1 | -√2/2 | |
| t | π/6 | π/4 | π/3 | |
| tg | √3/3 | 1 | √3 | |
| ctg | — | √3 | 1 | √3/3 |
sin x = b x = (-1)n arcsin b + πn
https://5-ege.ru/shpargalki-po-matematike/
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теоремасинусов: a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов: с2=a2+b2-2ab cos y
Неопределенные интегралы
∫ dx = x + C
∫ xn dx = (xn+1/n+1) + C
∫ dx/x2 = -1/x + C
∫ dx/√x = 2√x + C
∫ (kx+b) = 1/k F(kx + b)
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin2 x = -ctg + C
∫ dx/cos2 x = tg + C
∫ x r dx = x r+1/r+1 + C
Логарифмы
1. loga a = 1
2. loga 1 = 0
3. loga (bn) = n loga b
4. log An b = 1/n loga b
5. loga b = log c b/ log c a
6. loga b = 1/ log b a
| Градус | 30 | 45 | 60 | |
| sin | 1/2 | √2/2 | √3/2 | |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | √3/3 | 1 | √3 | |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | |
| -1/2 | -√2/2 | -√3/2 | -1 | |
| — | -√3 | -1 | √3/3 | |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x
tg 2x = 2 tg x/ 1 – tg2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin3 x
cos 3x = 4 cos3 x – 3 cos x
tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
c’ = 0 ()’ = 1/ 2
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x2) ( ln x)’ = 1/x
(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b2 – a2/4
3. Равносторонний треугольник
S = (a2/4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a2b sin C =
a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
5. Параллелограмм
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
tg(-x) = – tg x
ctg(-x) = – ctg x
tg (x + πk) = tg x
ctg (x + πk) = ctg x
tg (x ± π) = ± tg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin2 x + cos2 x =1
tg x · ctg x = 1
1 + tg2 x = 1/ cos2 x
1 + ctg2 x = 1/ sin2 x
tg2 (x/2) = 1 – cos x/ 1 + cos x
cos2 (x/2) = 1 + cos x/ 2
sin2 (x/2) = 1 – cos x/ 2
11. Шар: V=4/3 πR3 = 1/6 πD3
P = 4 πR2 = πD2
12. Шаровой сегмент
V = πh2 (R-1/3h) = πh/6(h2 + 3r2)
SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)
13. Шаровой слой
V = 1/6 πh3 + 1/2 π(r2 + h2)· h;
SБОК = 2 π·R·h
14. Шаровой сектор:
V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
(a≥0, b≥0)
(a≥0)
ax2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b2-4ac)
Если D>0, то x1,2 = -b± /2a
Теорема Виета
x1 + x2 = -b/a
x1 · x2 = c/a
Арифметическая прогрессия
a n+1 = an + d, где n – натуральное число
d – разность прогрессии;
a n= a 1 + (n – 1)·d – формула n-го члена
Сумма n членов
Sn = ((a 1 + a n )/2) · n
Sn = ((2a 1 + (n-1)d)/2) · n
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
r = a/ 2 tg 180/n
Окружность
L = 2 πR S = πR2
Площадь конуса
S БОК = πRL
S КОН= πR(L+R)
Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем:
Источник
Оглавление:
Таблица умножения
Таблица квадратов двухзначных чисел
Формулы сокращенного умножения
Квадратное уравнение и формула разложения квадратного трехчлена на множители
Свойства степеней и корней
Арифметическая прогрессия
Геометрическая прогрессия
Геометрия на плоскости (планиметрия)
Формулы с логарифмами
Тригонометрия
Тригонометрические уравнения
Геометрия в пространстве (стереометрия)
Координаты
Скачать расширенную версию «Все главные формулы по школьной математике»
Весь курс алгебры для ОГЭ в схемах и таблицах >>>
Весь курс геометрии для ОГЭ в схемах и таблицах >>>
Весь курс по реальной математике для ОГЭ >>>
Все графики функций >>>
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…

Формулы сокращенного умножения
К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:


#Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней.
В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

#Свойства степеней и корней
К оглавлению…
Основные свойства степеней:







Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:




Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:


Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
bn = b1 · q n-1
bn+1 =bn · q, где bn ≠ 0, q ≠ 0
q – знаменатель прогрессии

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:


