Полезные материалы для егэ по математике

Полный спектр материалов для подготовки к ЕГЭ по математике + решение задач по всем темам ЕГЭ. В каждой теме и каждой задаче есть свои секреты. О них вам может рассказать только очень хороший учитель или репетитор. Такой, как мы. Читайте, изучайте, скачивайте то, чего не найдёте в учебниках! Вы можете скачать весь курс бесплатно сразу или найти то, что ищете, на этой странице.

Актуальные видео по математике

Полный курс для подготовки к ЕГЭ по математике

New
Досрочный ЕГЭ 2020 года, Профильная математика.

New
Тренировочная работа 18 декабря 2019 года. Задача 19.
Учителю и репетитору: Методика, программы подготовки к ЕГЭ, поурочные планы.
Тесты и варианты ЕГЭ с решениями и ответами.
Алгебра – основные понятия и формулы.
Теория вероятностей.
Текстовые задачи.
Решение уравнений.
Решение неравенств.
Тригонометрия.
Планиметрия.
Стереометрия.
Функции и графики. Производная и первообразная.
«Экономические» задачи на ЕГЭ по математике.
Задачи с параметрами.
Нестандартные задачи на числа и их свойства.
Советы и рекомендации для подготовки к ЕГЭ по математике.

Профильный ЕГЭ по математике. Все задачи.

Задание 1. Простейшие текстовые задачи.
Задание 2. Чтение графиков и диаграмм.
Задание 3. Задачи на клетчатой бумаге или координатной плоскости.
Задание 4. Теория вероятностей. Основные понятия.
Задание 5. Простейшие уравнения.
Задание 6. Планиметрия.
Задание 7. Производная и первообразная.
Задание 8. Стереометрия.
Задание 9. Вычисления и преобразования.
Задание 10. Задачи с прикладным содержанием.
Задание 11. Текстовые задачи.
Задание 12. Исследование функций.
Задание 13. Уравнения на ЕГЭ по математике.
Задание 14. Стереометрия на ЕГЭ по математике.
Задание 15. Неравенства на ЕГЭ по математике.
Задание 16. Планиметрия на ЕГЭ по математике.
Задание 17. «Экономические» задачи на ЕГЭ по математике.
Задание 18. Задачи с параметрами на ЕГЭ по математике.
Задание 19. Задачи на числа и их свойства на ЕГЭ по математике Нестандартные задачи.
Таблица перевода баллов ЕГЭ, Профильный уровень.

ВАЖНО!

Как решалась задача №17 на ЕГЭ-2018?

Новая задача 19 Профильного ЕГЭ по математике (числа и их свойства), январь, восток

Новая задача 18 Профильного ЕГЭ по математике, Параметры, 24 января 2019, запад

Новая задача 16 Профильного ЕГЭ по математике, Геометрия, январь, запад

Задачи из сборника И. В. Ященко, 2020 год.

Вариант 6, задача 14
Вариант 8, задача 15
Вариант 32, задача 15
Вариант 36, задача 15
Вариант 2, задача 16
Вариант 4, задача 16
Вариант 6, задача 16
Вариант 8, задача 16
Вариант 12, задача 16
Вариант 1, задача 18
Вариант 5, задача 18
Вариант 11, задача 18
Вариант 26, задача 18
Вариант 36, задача 18
Вариант 27, задача 19

Новые варианты для подготовки к ЕГЭ и ОГЭ с ответами и решениями:

Выберите раздел:

Необходимый минимум

- Задача 1. Решается всегда!
- Задача 2. Чтение графика функции

Теория вероятностей. Основные понятия.
Видео бесплатно!
Теория вероятностей на ЕГЭ по математике. Полный курс..
Текстовые задачи. Движение и работа
Текстовые задачи. Проценты, сплавы, растворы…
ЕГЭ без ошибок. Вычисляем без калькулятора

Планиметрия

Геометрия. Формулы площадей фигур.
Программа по геометрии. Список необходимых фактов и теорем.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Тригонометрический круг: вся тригонометрия на одном рисунке
Внешний угол треугольника. Синус и косинус внешнего угла
Высота в прямоугольном треугольнике
Сумма углов треугольника
Углы при параллельных прямых и секущей
Высоты, медианы, биссектрисы треугольника
Четырёхугольники
Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция
Окружность. Центральный и вписанный угол
Касательная к окружности
Вписанные и описанные треугольники. Теорема синусов
Вписанные и описанные четырёхугольники
Правильный треугольник
Правильный шестиугольник
Векторы и операции над ними
Геометрия в школе: засада для абитуриента
Геометрический парадокс: Прямой угол равен тупому
Геометрический парадокс: Катет равен гипотенузе

Алгебра

Числовые множества
Степени и корни.
Что такое функция?
Чтение графика функции
Парабола и квадратные неравенства.
Степенная функция
Показательная функция
Показательные уравнения
Логарифмы
Логарифмическая функция
Элементарные функции и их графики
Показательные и логарифмические неравенства. 1
Показательные и логарифмические неравенства. 2
Число e
Видео бесплатно!
Производная функции. Геометрический смысл производной
Таблица производных и правила дифференцирования
Модуль числа
Уравнения и неравенства с модулем
Метод интервалов

Тригонометрия

Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрические формулы. Необходимый минимум
Видео бесплатно!
Формулы приведения
Тригонометрические формулы. Сводка для части 1
Тригонометрические формулы. Сводка для части 2
Тригонометрические функции
Простейшие тригонометрические уравнения, 1
Простейшие тригонометрические уравнения, 2
Тригонометрические уравнения

Стереометрия

Многогранники: формулы объема и площади поверхности
Тела вращения: формулы объема и площади поверхности
Задачи по стереометрии часть 1: Просто применяем формулы
Задачи по стереометрии часть 2: Приемы и секреты
Задача 14 (часть 2 ЕГЭ по математике). Программа по стереометрии
Плоскость в пространстве. Взаимное расположение плоскостей
Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые
Параллельность прямой и плоскости
Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости
Параллельность плоскостей
Угол между плоскостями. Перпендикулярность плоскостей
Угол и расстояние между скрещивающимися прямыми. Расстояние от точки до плоскости
Теорема о трёх перпендикулярах
Параллельное проецирование
Как строить чертежи в задачах по стереометрии
Векторы и метод координат в задаче 14, часть 2 ЕГЭ по математике
В.М. Мамаева. «Перпендикулярность. Книга для учащихся»
В.М. Мамаева. «Перпендикулярность. Книга для учителя»
В.М. Мамаева. «Тела вращения. Книга для учащихся»
В.М. Мамаева. «Тела вращения. Книга для учителя»

Часть 2 (задачи 13 — 19) на ЕГЭ по математике.

Видео

Задача 13: Уравнения на ЕГЭ по математике. Полный курс.

Видео

Задача 14: Стереометрия на ЕГЭ по математике. Полный курс. Оба метода — классика и векторы. Более 3 часов видео.

Видео

Задача 15: Неравенства на ЕГЭ по математике. Полный курс в двух частях.

Видео

Задача 16: Геометрия на ЕГЭ по математике. Полный курс. Более 5 часов видео.

Видео

Задачи по математике с экономическим содержанием. Задача 17 на ЕГЭ по математике и задачи олимпиад по экономике.

Видео бесплатно!

Задача 18: Параметры на ЕГЭ по математике. Графический метод.

Видео

Задача 18: Параметры на ЕГЭ по математике. Полный курс. Более 5 часов видео.
Задача 19 на числа и их свойства на ЕГЭ по математике.

Задача 19 на ЕГЭ по математике 2016 года. Решение.
Задача 19 на ЕГЭ по математике 2017 года. Решение.

Видео

Впервые! Видеокурс «Ключ к С6». Нестандартные задачи на ЕГЭ по математике.

Советы и рекомендации по подготовке к экзамену

Справочники для подготовки к ЕГЭ по математике
Методика подготовки к ЕГЭ по математике Анны Малковой
ЕГЭ по математике – советы и рекомендации
Репетитор по математике
Подготовиться к ЕГЭ самостоятельно и бесплатно
Математика и жизнь. Из воспоминаний бывалого студента.
Книги и учебники для подготовки к ЕГЭ по Математике
Как подготовиться к ЕГЭ по математике?
Как распределить время на ЕГЭ по математике
Подготовка к ЕГЭ по Математике с нуля
Самостоятельная подготовка к ЕГЭ по математике

Об этом сайте:

Каждый год на этом сайте готовятся к ЕГЭ сотни тысяч учащихся. Нас рекомендуют учителя и репетиторы. Автор сайта, на котором вы находитесь — репетитор-профессионал, ведущая курсов подготовки к ЕГЭ на высшие баллы, руководитель Образовательной компании «ЕГЭ-Студия» Анна Георгиевна Малкова.

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Источник

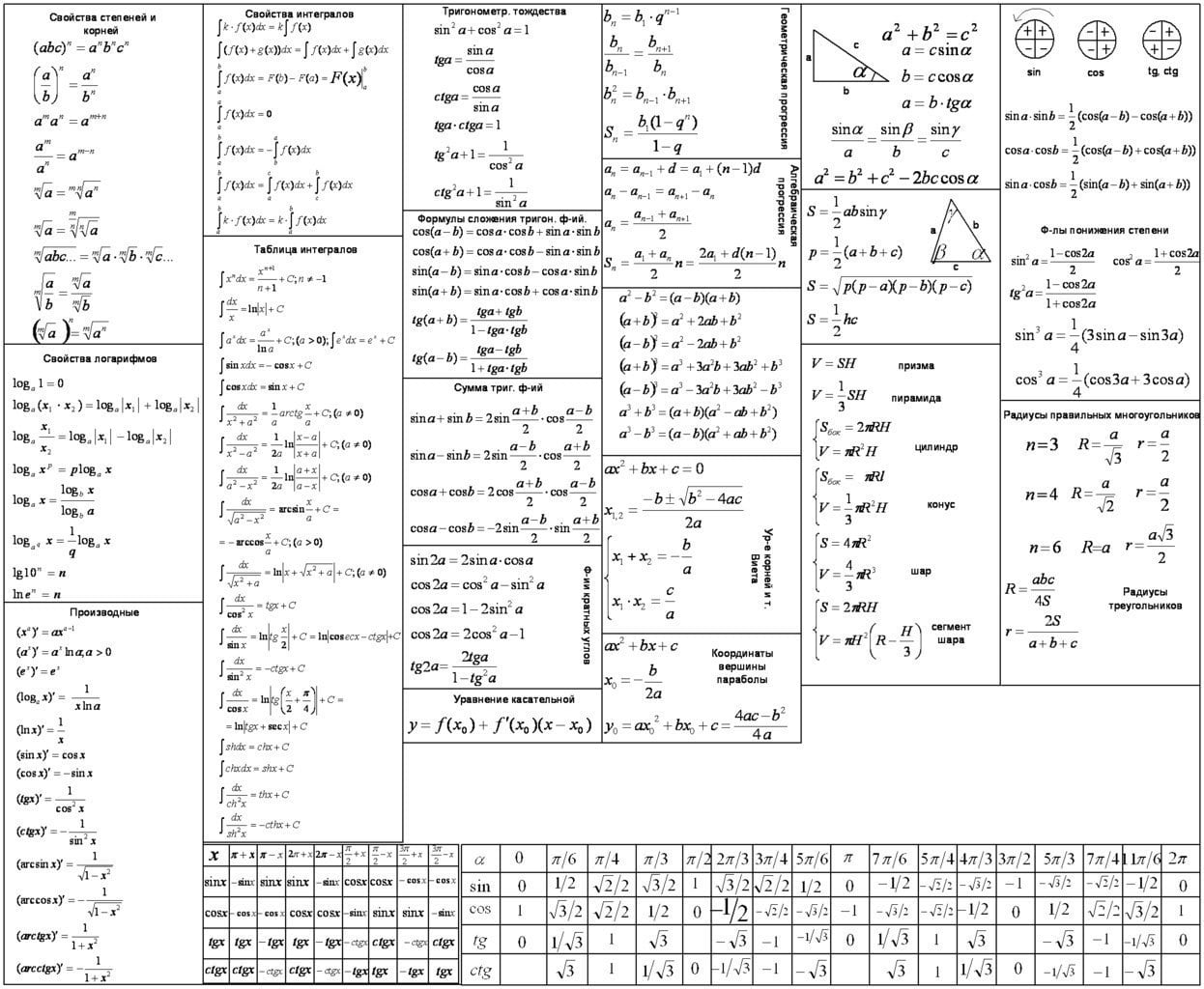
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.

Для начала шпаргалка в компактном виде:

шпаргалки по математике

Формулы сокращенного умножения

(а+b)2 = a2 + 2ab + b2

(а-b)2 = a2 – 2ab + b2

a2 – b2 = (a-b)(a+b)

a3 – b3 = (a-b)( a2 + ab + b2)

a3 + b3 = (a+b)( a2 – ab + b2)

(a + b)3 = a3 + 3a2b+ 3ab2+ b3

(a – b)3 = a3 – 3a2b+ 3ab2- b3

Свойства степеней

a0 = 1 (a≠0)

am/n = (a≥0, n ε N, m ε N)

a- r = 1/ a r (a>0, r ε Q)

a m · a n = a m + n

a m : a n = a m – n (a≠0)

(a m) n = a mn

(ab) n = a n b n

(a/b) n = a n/ b n

Первообразная

Если F’(x) = f(x), то F(x) – первообразная

для f(x)

Функция f(x) = Первообразная F(x)

k = kx + C

xn = xn+1/n+1 + C

1/x = ln |x| + C

ex = ex + C

ax = ax/ ln a + C

1/√x = 2√x + C

cos x = sin x + C

1/ sin2 x = – ctg x + C

1/ cos2 x = tg x + C

sin x = – cos x + C

1/ x2 = – 1/x

Геометрическая прогрессия

bn+1 = bn · q, где n ε N

q – знаменатель прогрессии

bn = b1 · qn – 1 – n-ый член прогрессии

Сумма n-ыхчленов

Sn = (b n q – b 1 )/q-1

Sn = b 1 (q n – 1 )/q-1

Модуль

|a| = a, если a≥0

-a, если a<0

Формулы cos и sin

sin (-x) = -sin x

cos (-x) = cos x

sin (x + π) = -sin x

cos (x + π) = -cos x

sin (x + 2πk) = sin x

cos (x + 2πk) = cos x

sin (x + π/2) = cos x

Объемы и поверхности тел

1. Призма, прямая или наклонная, параллелепипед V = S·h

2. Прямая призмаSБОК = p·h, p – периметр или длина окружности

3. Параллелепипед прямоугольный

V = a·b·c; P = 2(a·b + b·c + c·a)

P – полная поверхность

4. Куб: V = a3 ; P = 6 a2

5. Пирамида, правильная и неправ.

S = 1/3 S·h; S – площадь основания

6. Пирамида правильная S =1/2 p·A

A – апофема правильной пирамиды

7. Цилиндр круговой V = S·h = πr2h

8. Цилиндр круговой: SБОК = 2 πrh

9. Конус круговой: V=1/3 Sh = 1/3 πr2h

10. Конус круговой: SБОК = 1/2 pL= πrL

Тригонометрические уравнения

sin x = 0, x = πn

sin x = 1, x = π/2 + 2 πn

sin x = -1, x = – π/2 + 2 πn

cos x = 0, x = π/2 + 2 πn

cos x = 1, x = 2πn

cos x = -1, x = π + 2 πn

Теоремы сложения

cos (x +y) = cosx ·cosy – sinx ·siny

cos (x -y) = cosx ·cosy + sinx ·siny

sin (x +y) = sinx ·cosy + cosx ·siny

sin (x -y) = sinx ·cosy – cosx ·siny

tg (x ±y) = tg x ± tg y/ 1 -+ tg x ·tg y

ctg (x ±y) = tg x -+ tg y/ 1± tg x ·tg y

sin x ± sin y = 2 cos (x±y/2)· cos (x-+y/2)

cos x ± cosy = -2 sin (x±y/2)· sin (x-+y/2)

1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2

1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2

6. Трапеция

a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h

7. Квадрат

а – сторона, d – диагональ S = a2 = d2/2

8. Ромб

a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα

9. Правильный шестиугольник

a – сторона S = (3√3/2)a2

10. Круг

S = (L/2) r = πr2 = πd2/4

11. Сектор

S = (πr2/360) α

Правила дифференцирования

( f (x) + g (x) )’ = f ’(x) + g’(x)

(k(f(x))’ = kf ’ (x)

(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)

(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)

(xn)’ = nx n-1

(tg x)’ = 1/ cos2 x

(ctg x)’ = – 1/ sin2 x

(f (kx + m))’ = kf ’(kx + m)

Уравнение касательной к графику функции

y = f ’(a) (x-a) + f(a)

Площадь S фигуры, ограниченной прямыми x=a, x=b

S = ∫( f(x) – g(x)) dx

Формула Ньютона-Лебница

∫ab f(x) dx = F(b) – F (a)

t	π/4	π/2	3π/4	π
cos	√2/2		-√2/2	1
sin	√2/2	1	√2/2
t	5π/4	3π/2	7π/4	2π
cos	-√2/2		√2/2	1
sin	-√2/2	-1	-√2/2
t		π/6	π/4	π/3
tg		√3/3	1	√3
ctg	—	√3	1	√3/3

sin x = b x = (-1)n arcsin b + πn

https://5-ege.ru/shpargalki-po-matematike/

cos x = b x = ± arcos b + 2 πn

tg x = b x = arctg b + πn

ctg x = b x = arcctg b + πn

Теоремасинусов: a/sin α = b/sin β = c/sin γ = 2R

Теорема косинусов: с2=a2+b2-2ab cos y

Неопределенные интегралы

∫ dx = x + C

∫ xn dx = (xn+1/n+1) + C

∫ dx/x2 = -1/x + C

∫ dx/√x = 2√x + C

∫ (kx+b) = 1/k F(kx + b)

∫ sin x dx = – cos x + C

∫ cos x dx = sin x + C

∫ dx/sin2 x = -ctg + C

∫ dx/cos2 x = tg + C

∫ x r dx = x r+1/r+1 + C

Логарифмы

1. loga a = 1

2. loga 1 = 0

3. loga (bn) = n loga b

4. log An b = 1/n loga b

5. loga b = log c b/ log c a

6. loga b = 1/ log b a

Градус		30	45	60
sin		1/2	√2/2	√3/2
cos	1	√3/2	√2/2	1/2
tg		√3/3	1	√3
t	π/6	π/3	2π/3	5π/6
cos	√3/2	1/2	-1/2	-√3/2
sin	1/2	√3/2	√3/2	1/2
90	*120*	*135*	*150*	*180*
1	√3/2	√2/2	1/2
	-1/2	-√2/2	-√3/2	-1
—	-√3	-1	√3/3
t	7π/6	4π/3	5π/3	11π/6
cos	-√3/2	-1/2	1/2	√3/2
sin	-1/2	-√3/2	-√3/2	-1/2

Формулы двойного аргумента

cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x

sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x

tg 2x = 2 tg x/ 1 – tg2 x

ctg 2x = ctg 2 x – 1/ 2 ctg x

sin 3x = 3 sin x – 4 sin3 x

cos 3x = 4 cos3 x – 3 cos x

tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x

sin s cos t = (sin (s+t) + sin (s+t))/2

sin s sin t = (cos (s-t) – cos (s+t))/2

cos s cos t = (cos (s+t) + cos (s-t))/2

Формулы дифференцирования

c’ = 0 ()’ = 1/ 2

x’ = 1 (sin x)’ = cos x

(kx + m)’ = k (cos x)’ = – sin x

(1/x)’ = – (1/x2) ( ln x)’ = 1/x

(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a

Площади плоских фигур

1. Прямоугольный треугольник

S = 1/2 a·b (a, b – катеты)

2. Равнобедренный треугольник

S = (a/2)·√ b2 – a2/4

3. Равносторонний треугольник

S = (a2/4)·√3 (a – сторона)

4. Произвольный треугольник

a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2

S = 1/2 a·h = 1/2 a2b sin C =

a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)

5. Параллелограмм

a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α

cos (x + π/2) = -sin x

Формулы tg и ctg

tg x = sin x/ cos x; ctg x = cos x/sin x

tg(-x) = – tg x

ctg(-x) = – ctg x

tg (x + πk) = tg x

ctg (x + πk) = ctg x

tg (x ± π) = ± tg x

ctg (x ± π) = ± ctg x

tg (x + π/2) = – ctg x

ctg (x + π/2) = – tg x

sin2 x + cos2 x =1

tg x · ctg x = 1

1 + tg2 x = 1/ cos2 x

1 + ctg2 x = 1/ sin2 x

tg2 (x/2) = 1 – cos x/ 1 + cos x

cos2 (x/2) = 1 + cos x/ 2

sin2 (x/2) = 1 – cos x/ 2

11. Шар: V=4/3 πR3 = 1/6 πD3

P = 4 πR2 = πD2

12. Шаровой сегмент

V = πh2 (R-1/3h) = πh/6(h2 + 3r2)

SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)

13. Шаровой слой

V = 1/6 πh3 + 1/2 π(r2 + h2)· h;

SБОК = 2 π·R·h

14. Шаровой сектор:

V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе

Формула корней квадратного уравнения

(a≥0, b≥0)

(a≥0)

ax2 + bx + c = 0 (a≠0)

Если D=0, то x = -b/2a (D = b2-4ac)

Если D>0, то x1,2 = -b± /2a

Теорема Виета

x1 + x2 = -b/a

x1 · x2 = c/a

Арифметическая прогрессия

a n+1 = an + d, где n – натуральное число

d – разность прогрессии;

a n= a 1 + (n – 1)·d – формула n-го члена

Сумма n членов

Sn = ((a 1 + a n )/2) · n

Sn = ((2a 1 + (n-1)d)/2) · n

Радиус описанной окружности около многоугольника

R = a/ 2 sin 180/n

Радиус вписанной окружности

r = a/ 2 tg 180/n

Окружность

L = 2 πR S = πR2

Площадь конуса

S БОК = πRL

S КОН= πR(L+R)

Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.

Скачать шпаргалки по математике

Скачать всё это в компактном виде: matematika-shpory.doc.

Рекомендуем:

Источник

Формулы для профильного ЕГЭ-2020 по математике

Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия

Формулы сокращённого умножения

`(a + b)^2=a^2 + 2ab + b^2`
`(a − b)^2=a^2 − 2ab + b^2`
`a^2 − b^2=(a + b)(a − b)`

`a^3 + b^3=(a + b)(a^2 − ab + b^2)`
`a^3 − b^3=(a − b)(a^2 + ab + b^2)`

`(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3`
`(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3`

Прогрессии

Арифметическая прогрессия:

`a_n=a_(n-1)+d`

`a_n=a_1+(n-1)*d`

`S_n=((a_1+a_n)*n)/2`

Геометрическая прогрессия:

`b_n=b_(n-1)*q`

`b_n=b_1*q^(n-1)`

`S_n=((q^n-1)*b_1)/(q-1)`

Бесконечно убывающая: `S=b_1/(1-q)`

Вероятность

Вероятность события A:	`P(A)=m/n`

События происходят A и B происходят одновременно	`A*B`
Независимые события:	`P(AB)=P(A)P(B)`
Зависимые события:	`P(AB)=P(A)P(B\|A)`

Происходит или событие A, или B	`A+B`
Несовместные события:	`P(A+B)=P(A)+P(B)`
Совместные события:	`P(A+B)=P(A)+P(B)-P(A*B)`

Свойства степеней

`a^0=1`	`a^1=a`
`a^(-1)=1/a`	`a^(-n)=1/a^n`
`a^(1/2)=sqrt(a)`	`a^(1/n)=root(n)(a)`
`a^m*a^n=a^(m+n)`	`a^m/a^n=a^(m-n)`
`(ab)^n=a^nb^n`	`(a/b)^n=a^n/b^n`
`(a^m)^n=a^(m*n)`	`a^(m/n)=root(n)(a^m)`

Свойства логарифмов

`log_ab=c«a^c=b`
`log_a1=0`
`log_aa=1`
`log_a(b*c)=log_ab+log_ac`
`log_a(b/c)=log_ab-log_ac`
`log_ab^n=n*log_ab`
`log_(a^m)b=1/m*log_ab`
`log_ab=1/(log_ba)`
`log_ab=(log_cb)/(log_ca)`
`a^(log_cb)=b^(log_ca)`
`a^(log_ab)=b`

Тригонометрия

`alpha`	`0`	`pi/6`	`pi/4`	`pi/3`	`pi/2`	`pi`	`(3pi)/2`	`2pi`
`alpha`	`0^circ`	`30^circ`	`45^circ`	`60^circ`	`90^circ`	`180^circ`	`270^circ`	`360^circ`
`sinalpha`	`0`	`1/2`	`sqrt(2)/2`	`sqrt(3)/2`	`1`	`0`	`-1`	`0`
`cosalpha`	`1`	`sqrt(3)/2`	`sqrt(2)/2`	`1/2`	`0`	`-1`	`0`	`1`
`text(tg)alpha`	`0`	`sqrt(3)/3`	`1`	`sqrt(3)`	`infty`	`0`	`infty`	`0`
`text(ctg)alpha`	`infty`	`sqrt(3)`	`1`	`sqrt(3)/3`	`0`	`infty`	`0`	`infty`

Основные соотношения

`sin^2alpha+cos^2alpha=1`
`text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)^2alpha)`

Формулы двойного угла

`cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}`
`sin2alpha=2sinalphacosalpha`
`text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)`

Формулы суммы и разности аргументов

`sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta`

`cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta`

`text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)`

Преобразование суммы и разности в произведение

`sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)`

`cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)`

`cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)`

Формулы половинного аргумента

`sin(alpha/2)=+-sqrt((1-cosalpha)/2)`
`cos(alpha/2)=+-sqrt((1+cosalpha)/2)`
`text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)`

Обратные тригонометрические функции

`sinx=A`	`x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}`	`kinZZ`
`cosx=A`	`x=±arccosA + 2pik`	`kinZZ`
`tg x=A`	`x=text(arctg) A + pik`	`kinZZ`
`ctg x=A`	`x=text(arcctg) A + pik`	`kinZZ`

Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.

Производные

Основные правила дифференцирования

`(u+-v)’=u’+-v’`
`(uv)’=u’v+u*v’`
`(u/v)^’=(u’v-uv’)/v^2`
`[f(g(x))]’=f'(g(x))*g'(x)`

Уравнение касательной

`y=f(x_0)+f'(x_0)*(x-x_0)`

Производные элементарных функций

`C’=0`	`(C*x)’=C`
`(x^m)’=mx^(m-1)`	`(sqrtx)’=1/(2sqrtx)`
`(1/x)^’=-1/x^2`
`(e^x)’=e^x`	`(lnx)’=1/x`
`(a^x)’=a^x*lna`	`(log_ax)’=1/(xlna)`
`(sinx)’=cosx`	`(cosx)’=-sinx`
`(text(tg)x)’=1/cos^2x`	`(text(ctg)x)’=-1/sin^2x`
`(arcsinx)’=1/sqrt(1-x^2)`	`(arccosx)’=-1/sqrt(1-x^2)`
`(text(arctg))=1/(1+x^2)’`	`(text(arcctg))’=-1/(1+x^2)`

Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).

Первообразные

Первообразная:	`F'(x)=f(x)`
Неопределённый интеграл:	`intf(x)dx=F(x)+C`
Определённый интеграл (формула Ньютона-Лейбница):	`int_a^bf(x)dx=F(b)-F(a)`

Таблица первообразных

`f(x)`	`F(x)`	`F(x)`
`a`	`ax`
`x^n`	`x^(n+1)/(n+1)`	`1/x`	`lnx`
`e^x`	`e^x`	`a^x`	`a^x/lna`
`sinx`	`-cosx`	`cosx`	`sinx`
`1/cos^2x`	`text(tg)x`	`1/sin^2x`	`-text(ctg)x`
`1/(x^2+a^2)`	`1/atext(arctg)x/a`	`1/(x^2-a^2)`	`1/(2a)ln\|(x-a)/(x+a)\|`
`1/sqrt(a^2-x^2)`	`text(arcsin)x/a`	`1/sqrt(x^2+a)`	`ln\|x+sqrt(x^2+a)\|`

Геометрия

Планиметрия (2D)

Площади фигур:

Окружность:	`S=pir^2`
Треугольник:	`S=1/2ah`
Параллелограмм:	`S=ah`
Четырёхугольник:	`S=1/2d_1d_2sinvarphi`
Трапеция:	`S=(a+b)/2*h`

Стереометрия (3D)

Призма:	`V=S_(осн)h`
Пирамида:	`V=1/3S_(осн)h`
Конус:	`V=1/3S_(осн)h`
`S_(бок)=pirl`
Цилиндр:	`V=pir^2h`
	`S_(бок)=2pirh`
Шар:	`V=4/3pir^3`
`S=4pir^2`

Источник

ÐÐ²ÑÐ¾ÑÑ Ð¸ Ð¼ÐµÑÐ¾Ð´Ð¸ÑÑÑ

Источник

Полезные материалы для егэ по математике

Полный курс для подготовки к ЕГЭ по математике

Профильный ЕГЭ по математике. Все задачи.

Задачи из сборника И. В. Ященко, 2020 год.

Новые варианты для подготовки к ЕГЭ и ОГЭ с ответами и решениями:

Выберите раздел:

Необходимый минимум

Планиметрия

Алгебра

Тригонометрия

Стереометрия

Часть 2 (задачи 13 — 19) на ЕГЭ по математике.

Советы и рекомендации по подготовке к экзамену

Об этом сайте:

Скачать шпаргалки по математике

Формулы для профильного ЕГЭ-2020 по математике

Формулы сокращённого умножения

Прогрессии

Арифметическая прогрессия:

Геометрическая прогрессия:

Вероятность

Свойства степеней

Свойства логарифмов

Тригонометрия

Основные соотношения

Формулы двойного угла

Формулы суммы и разности аргументов

Преобразование суммы и разности в произведение

Формулы половинного аргумента

Обратные тригонометрические функции

Производные

Основные правила дифференцирования

Уравнение касательной

Производные элементарных функций

Первообразные

Таблица первообразных

Геометрия

Планиметрия (2D)

Стереометрия (3D)

ÐÐÐ­ Ð¿Ð¾ Ð¼Ð°ÑÐµÐ¼Ð°ÑÐ¸ÐºÐµ. ÐÐ°Ð·Ð¾Ð²ÑÐ¹ ÑÑÐ¾Ð²ÐµÐ½Ñ.

ÐÐÐ­ Ð¿Ð¾ Ð¼Ð°ÑÐµÐ¼Ð°ÑÐ¸ÐºÐµ. ÐÑÐ¾ÑÐ¸Ð»ÑÐ½ÑÐ¹ ÑÑÐ¾Ð²ÐµÐ½Ñ.

ÐÐ²ÑÐ¾ÑÑ Ð¸ Ð¼ÐµÑÐ¾Ð´Ð¸ÑÑÑ

ÐÐÐ Ð¿Ð¾ Ð¼Ð°ÑÐµÐ¼Ð°ÑÐ¸ÐºÐµ. ÐÐ°Ð·Ð¾Ð²ÑÐ¹ ÑÑÐ¾Ð²ÐµÐ½Ñ.

ÐÐÐ Ð¿Ð¾ Ð¼Ð°ÑÐµÐ¼Ð°ÑÐ¸ÐºÐµ. ÐÑÐ¾ÑÐ¸Ð»ÑÐ½ÑÐ¹ ÑÑÐ¾Ð²ÐµÐ½Ñ.

ÐÐ²ÑÐ¾ÑÑ Ð¸ Ð¼ÐµÑÐ¾Ð´Ð¸ÑÑÑ