Полезный момент на валу асинхронного двигателя

Ðàáî÷èå õàðàêòåðèñòèêè àñèíõðîííîãî äâèãàòåëÿ ïðåäñòàâëÿþò ñîáîé ãðàôè÷åñêè âûðàæåííûå çàâèñèìîñòè ÷àñòîòû âðàùåíèÿ n2, ÊÏÄ η, ïîëåçíîãî ìîìåíòà (ìîìåíòà íà âàëó) Ì2, êîýôôèöèåíòà ìîùíîñòè cos φ, è òîêà ñòàòîðà I1 îò ïîëåçíîé ìîùíîñòè Ð2 ïðè U1 = const f1 = const.
Ñêîðîñòíàÿ õàðàêòåðèñòèêà n2 = f(P2). ×àñòîòà âðàùåíèÿ ðîòîðà àñèíõðîííîãî äâèãàòåëÿ n2 = n1(1 — s).
Ñêîëüæåíèå s = Pý2/Pýì, ò. å. ñêîëüæåíèå àñèíõðîííîãî äâèãàòåëÿ, à ñëåäîâàòåëüíî, è åãî ÷àñòîòà âðàùåíèÿ îïðåäåëÿþòñÿ îòíîøåíèåì ýëåêòðè÷åñêèõ ïîòåðü â ðîòîðå ê ýëåêòðîìàãíèòíîé ìîùíîñòè. Ïðåíåáðåãàÿ ýëåêòðè÷åñêèìè ïîòåðÿìè â ðîòîðå â ðåæèìå õîëîñòîãî õîäà, ìîæíî ïðèíÿòü Ðý2 = 0, à ïîýòîìó s ≈ 0 è n20 ≈ n1.
Ïî ìåðå óâåëè÷åíèÿ íàãðóçêè íà âàëó àñèíõðîííîãî äâèãàòåëÿ îòíîøåíèå s = Pý2/Pýì ðàñòåò, äîñòèãàÿ çíà÷åíèé 0,01 — 0,08 ïðè íîìèíàëüíîé íàãðóçêå.  ñîîòâåòñòâèè ñ ýòèì çàâèñèìîñòü n2 = f(P2) ïðåäñòàâëÿåò ñîáîé êðèâóþ, ñëàáî íàêëîíåííóþ ê îñè àáñöèññ. Îäíàêî ïðè óâåëè÷åíèè àêòèâíîãî ñîïðîòèâëåíèÿ ðîòîðà äâèãàòåëÿ r2′ óãîë íàêëîíà ýòîé êðèâîé óâåëè÷èâàåòñÿ.  ýòîì ñëó÷àå èçìåíåíèÿ ÷àñòîòû àñèíõðîííîãî äâèãàòåëÿ n2 ïðè êîëåáàíèÿõ íàãðóçêè Ð2 âîçðàñòàþò. Îáúÿñíÿåòñÿ ýòî òåì, ÷òî ñ óâåëè÷åíèåì r2′ âîçðàñòàþò ýëåêòðè÷åñêèå ïîòåðè â ðîòîðå.
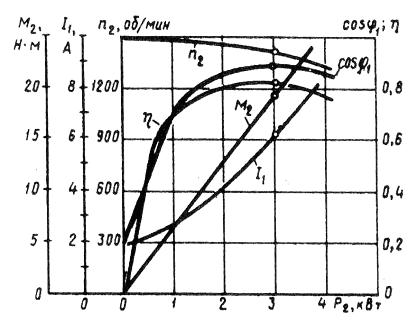
Ðèñ. 1. Ðàáî÷èå õàðàêòåðèñòèêè àñèíõðîííîãî äâèãàòåëÿ äâèãàòåëÿ
Çàâèñèìîñòü Ì2 =f(P2). Çàâèñèìîñòü ïîëåçíîãî ìîìåíòà íà âàëó àñèíõðîííîãî äâèãàòåëÿ Ì2 îò ïîëåçíîé ìîùíîñòè Ð2 îïðåäåëÿåòñÿ âûðàæåíèåì M2 = Ð2/ ω2 = 60 P2/ (2πn2) = 9,55Ð2/ n2,
ãäå Ð2 ïîëåçíàÿ ìîùíîñòü, Âò; ω2 = 2πf 2/ 60 óãëîâàÿ ÷àñòîòà âðàùåíèÿ ðîòîðà.
Èç ýòîãî âûðàæåíèÿ ñëåäóåò, ÷òî åñëè n2 = const, òî ãðàôèê Ì2 =f2(Ð2) ïðåäñòàâëÿåò ñîáîé ïðÿìóþ ëèíèþ. Íî â àñèíõðîííîì äâèãàòåëå ñ óâåëè÷åíèåì íàãðóçêè Ð2 ÷àñòîòà âðàùåíèÿ ðîòîðà óìåíüøàåòñÿ, à ïîýòîìó ïîëåçíûé ìîìåíò íà âàëó Ì2 ñ óâåëè÷åíèåì íàãðóçêè âîçðàñòàåò íå ñêîëüêî áûñòðåå íàãðóçêè, à ñëåäîâàòåëüíî, ãðàôèê Ì2 =f (P2) èìååò êðèâîëèíåéíûé âèä.
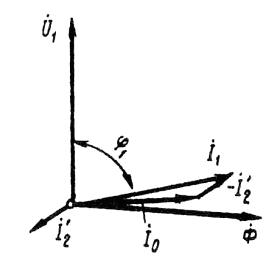
Ðèñ. 2. Âåêòîðíàÿ äèàãðàììà àñèíõðîííîãî äâèãàòåëÿ ïðè íåáîëüøîé íàãðóçêå
Çàâèñèìîñòü cos φ1 = f (P2).  ñâÿçè ñ òåì ÷òî òîê ñòàòîðà àñèíõðîííîãî äâèãàòåëÿ I1 èìååò ðåàêòèâíóþ (èíäóêòèâíóþ) ñîñòàâëÿþùóþ, íåîáõîäèìóþ äëÿ ñîçäàíèÿ ìàãíèòíîãî ïîëÿ â ñòàòîðå, êîýôôèöèåíò ìîùíîñòè àñèíõðîííûõ äâèãàòåëåé ìåíüøå åäèíèöû. Íàèìåíüøåå çíà÷åíèå êîýôôèöèåíòà ìîùíîñòè ñîîòâåòñòâóåò ðåæèìó õîëîñòîãî õîäà. Îáúÿñíÿåòñÿ ýòî òåì, ÷òî òîê õîëîñòîãî õîäà ýëåêòðîäâèãàòåëÿ I0 ïðè ëþáîé íàãðóçêå îñòàåòñÿ ïðàêòè÷åñêè íåèçìåííûì. Ïîýòîìó ïðè ìàëûõ íàãðóçêàõ äâèãàòåëÿ òîê ñòàòîðà íåâåëèê è â çíà÷èòåëüíîé ÷àñòè ÿâëÿåòñÿ ðåàêòèâíûì (I1 ≈ I0).  ðåçóëüòàòå ñäâèã ïî ôàçå òîêà ñòàòîðà îòíîñèòåëüíî íàïðÿæåíèÿ ïîëó÷àåòñÿ çíà÷èòåëüíûì (φ1 ≈ φ0), ëèøü íåìíîãèì ìåíüøå 90° (ðèñ. 2).
Êîýôôèöèåíò ìîùíîñòè àñèíõðîííûõ äâèãàòåëåé â ðåæèìå õîëîñòîãî õîäà îáû÷íî íå ïðåâûøàåò 0,2. Ïðè óâåëè÷åíèè íàãðóçêè íà âàëó äâèãàòåëÿ ðàñòåò àêòèâíàÿ ñîñòàâëÿþùàÿ òîêà I1 è êîýôôèöèåíò ìîùíîñòè âîçðàñòàåò, äîñòèãàÿ íàèáîëüøåãî çíà÷åíèÿ (0,80 — 0,90) ïðè íàãðóçêå, áëèçêîé ê íîìèíàëüíîé. Äàëüíåéøåå óâåëè÷åíèå íàãðóçêè íà âàëó äâèãàòåëÿ ñîïðîâîæäàåòñÿ óìåíüøåíèåì cos φ1 ÷òî îáúÿñíÿåòñÿ âîçðàñòàíèåì èíäóêòèâíîãî ñîïðîòèâëåíèÿ ðîòîðà (x2s) çà ñ÷åò óâåëè÷åíèÿ ñêîëüæåíèÿ, à ñëåäîâàòåëüíî, è ÷àñòîòû òîêà â ðîòîðå.
 öåëÿõ ïîâûøåíèÿ êîýôôèöèåíòà ìîùíîñòè àñèíõðîííûõ äâèãàòåëåé ÷ðåçâû÷àéíî âàæíî, ÷òîáû äâèãàòåëü ðàáîòàë âñåãäà èëè ïî êðàéíåé ìåðå çíà÷èòåëüíóþ ÷àñòü âðåìåíè ñ íàãðóçêîé, áëèçêîé ê íîìèíàëüíîé. Ýòî ìîæíî îáåñïå÷èòü ëèøü ïðè ïðàâèëüíîì âûáîðå ìîùíîñòè äâèãàòåëÿ. Åñëè æå äâèãàòåëü ðàáîòàåò çíà÷èòåëüíóþ ÷àñòü âðåìåíè íåäîãðóæåííûì, òî äëÿ ïîâûøåíèÿ cos φ1, öåëåñîîáðàçíî ïîäâîäèìîå ê äâèãàòåëþ íàïðÿæåíèå U1 óìåíüøèòü. Íàïðèìåð, â äâèãàòåëÿõ, ðàáîòàþùèõ ïðè ñîåäèíåíèè îáìîòêè ñòàòîðà òðåóãîëüíèêîì, ýòî ìîæíî ñäåëàòü ïåðåñîåäèíèâ îáìîòêè ñòàòîðà â çâåçäó, ÷òî âûçîâåò óìåíüøåíèå ôàçíîãî íàïðÿæåíèÿ â ðàç. Ïðè ýòîì ìàãíèòíûé ïîòîê ñòàòîðà, à ñëåäîâàòåëüíî, è íàìàãíè÷èâàþùèé òîê óìåíüøàþòñÿ ïðèìåðíî â ðàç. Êðîìå òîãî, àêòèâíàÿ ñîñòàâëÿþùàÿ òîêà ñòàòîðà íåñêîëüêî óâåëè÷èâàåòñÿ. Âñå ýòî ñïîñîáñòâóåò ïîâûøåíèþ êîýôôèöèåíòà ìîùíîñòè äâèãàòåëÿ.
Íà ðèñ. 3 ïðåäñòàâëåíû ãðàôèêè çàâèñèìîñòè cos φ1, àñèíõðîííîãî äâèãàòåëÿ îò íàãðóçêè ïðè ñîåäèíåíèè îáìîòîê ñòàòîðà çâåçäîé (êðèâàÿ 1) è òðåóãîëüíèêîì (êðèâàÿ 2).
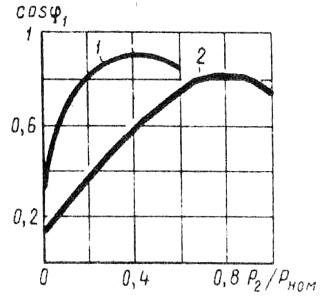
Ðèñ. 3. Çàâèñèìîñòü cos φ1,îò íàãðóçêè ïðè ñîåäèíåíèè îáìîòêè ñòàòîðà äâèãàòåëÿ çâåçäîé (1) è òðåóãîëüíèêîì (2)

Источник
ПРАКТИЧЕСКАЯ РАБОТА №8
«Расчет рабочих характеристик асинхронного двигателя»
ЦЕЛЬ РАБОТЫ: построить упрощенную круговую диаграмму трехфазного асинхронного двигателя и определить параметры, соответствующие его номинальному режиму работы.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Рабочие характеристики асинхронного двигателя (рис. 8.1) представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.
Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 — s).
s = Pэ2/ Pэм, (8.1), т. е. скольжение двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности Рэм. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1.
Рис. 8.1. Рабочие характеристики асинхронного двигателя

По мере увеличения нагрузки на валу двигателя отношение (8.1) растет, достигая значений 0,01—0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора r2′ угол наклона этой кривой увеличивается. В этом случае изменения частоты вращения n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2′ возрастают электрические потери в роторе.
Зависимость М2 =f(P2). Зависимость полезного момента на валу двигателя М2 от полезной мощности Р2 определяется выражением
M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2, (8.2)
где Р2 — полезная мощность, Вт; ω2 = 2πf 2/ 60 — угловая частота вращения ротора.
Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.
Рис. 8.2. Векторная диаграмма асинхронного двигателя при небольшой нагрузке
Зависимость cosφ1 = f (P2). В связи с тем что ток статора I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму х.х. Объясняется это тем, что ток х.х. I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора , относительно напряжения , получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рис. 8.2). Коэффициент мощности асинхронных двигателей в режиме х.х. обычно не превышает 0,2.
Рис. 8.3. Зависимость cos φ1,от нагрузки при соединении обмотки статора звездой (1) и треугольником (2)
При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80—0,90) при нагрузке, близкой к номинальной. Дальнейшее увелиичение нагрузки сопровождается уменьшением cosφ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе. В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cosφ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя. На рис. 8.3 представлены графики зависимости cosφ1, асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
Решить задачу №1. По рабочим характеристикам трехфазных асинхронных двигателей, приведенным в Приложении, и данным табл. 8.1 по каждому из предлагаемых вариантов требуется определить:
а) параметры двигателя в номинальном режиме работы — ток статора I1ном, КПД ηном, коэффициент мощности cos φном, скольжение sном, частоту вращения nном, потребляемую мощность Р1ном;
б) максимальное значение КПД ηmах и соответствующие этому КПД нагрузку Р2, выразив ее в долях от номинальной Рном;
в) отношение переменных потерь Рпер.ном к постоянным потерям Рпост при номинальной нагрузке;
г) активное сопротивление фазы обмотки статора rх.
Таблица 8.1.
Параметр
Варианты
1
2
3
4
5
6
Рисунок (см. приложение 2)
П. 2.1
П. 2.2
П. 2.3
П. 2.4
П. 2.5
П. 2.6
Рном , кВт
250
2,8
7,5
160
4,0
45
Напряжение сети U1л, В
660
220
380
380
220
380
Схема соединения обмотки статора
Y
Δ
Y
Δ
Δ
Y
2 р
4
4
4
4
4
4
Решение:
определить параметры двигателя при номинальном режиме (см. рис. П. 2.1 ): полезную мощность двигателя Рном , ток статора I1ном ,скольжение sном , частоту вращения пном , коэффициент полезного действия ηном , коэффициент мощности cos φ1ном , потребляемая мощность Р1ном= Рном / η;
определить максимальное значение КПД ηmах соответствует нагрузке Р2 = 150 0,6Рном (см. рис. П.2.1).
определить потребляемую двигателем мощность при нагрузке 0,6Рном : Р1/ηmах;
определить сумму потерь при нагрузке 0,6Рном :
 ;
;определить величину постоянных потерь:
 ;
;определить суммарные потери двигателя при номинальной нагрузке:
 ;
;определить переменные потери в режиме номинальной нагрузки:
 ;
;определить отношение переменных потерь к постоянным при номинальной нагрузке:
 ;
;определить добавочные потери при номинальной нагрузке:
 ;
;определить момент холостого хода:
 ;
;определить номинальный момент на валу двигателя:
 ;
;определить электромагнитный момент в номинальном режиме:
 ;
;определить электромагнитную мощность в номинальном режиме:
 ;
;определить величину электрических потерь в обмотке ротора в режиме номинальной нагрузки:
 ;
;определить величину электрических потерь в обмотке статора в режиме номинальной нагрузки:
 ;
;определить активное сопротивление фазы обмотки статора:
 .
.
Решить задачу №2. Построить упрощенную круговую диаграмму трехфазного асинхронного двигателя и определить параметры, соответствующие его номинальному режиму работы. Необходимые для построения диаграммы данные приведены в табл. 8.2: номинальная мощность Рном; напряжение на обмотке статора (фазное) U1ф; номинальный ток статора (фазный) I1ф; число полюсов 2р; активное сопротивление фазной обмотки статора при рабочей температуре rx; ток холостого хода (фазный) I0ф; мощность холостого хода Р0; мощность идеального холостого хода
 механические потери Рмех; коэффициент мощности холостого хода сos φ0; мощность короткого замыкания Рк; напряжение короткого замыкания (фазное) UK; коэффициент мощности короткого замыкания cos φк; частота тока 50 Гц.
механические потери Рмех; коэффициент мощности холостого хода сos φ0; мощность короткого замыкания Рк; напряжение короткого замыкания (фазное) UK; коэффициент мощности короткого замыкания cos φк; частота тока 50 Гц.
Таблица 8.2.
Параметр
Варианты
1
2
3
4
5
6
Рном, кВт
3,0
12
70
22
250
16
U1ф, В
220
220
220
220
1730
220
I1ф, А
6,3
25
190
54
60
40
2 р
4
4
4
8
6
8
r1ф, Ом
1,7
0,32
0,035
0,15
0,68
0,15
I0ф , А
1,83
9,7
55
32,8
17,5
9,6
Р, Вт
300
565
6500
1340
10 750
950
Р’, Вт
283
475
6180
1120
10125
890
Рмех,ВТ
200
250
600
370
1350
270
сos φ0
0,24
0,10
0,20
0,064
0,12
0,15
Рк,Вт
418
1780
9500
2360
12 160
1740
Uк.ф,В
59,5
57,8
58,0
44,0
360
42,0
cos φк
0,37
0,34
0,30
0,33
0,25
0,34
Решение:
определить углы фазового сдвига токов холостого хода
 и короткого замыкания
и короткого замыкания  относительно напряжения
относительно напряжения  (рис. 8.1): φ0=arccos(сos φ0), φк=arccos(сos φк);
(рис. 8.1): φ0=arccos(сos φ0), φк=arccos(сos φк);определить ток короткого замыкания (фазный), приведенный к номинальному напряжению:
 ;
;принять масштаб тока исходя из размеров листа бумаги, на котором предполагается построение диаграммы; например, если применяется лист форматом А4 (210 х 297 мм), то масштаб тока m1=0,1 А/мм;
определить длину векторов тока: холостого хода —
 ; номинального тока статора —
; номинального тока статора —  ; тока короткого замыкания —
; тока короткого замыкания —  ;
;определить масштабы мощности и момента:
 ;
; ;
;на оси ординат из точки О построить вектор напряжения U1ф произвольной длины и под углом φ0 к оси ординат строим вектор тока холостого хода ОН и под углом φк строим вектор тока короткого замыкания ОК;
из точки Н параллельно оси абсцисс провести прямую, на которой отложить отрезок НС, равный диаметру окружности токов
 , где
, где  ;
;из точки O1, лежащей посередине диаметра окружности, радиусом НС/2 провести полуокружность токов. При этом точки Н и К оказываются на этой полуокружности. Соединить точки Н и К и получить линию полезной мощности НК;
на окружности токов отметить точку D1 (точка номинального режима нагрузки двигателя). Для этого из точки О отложить отрезок OD1;
на средней части отрезка О1С отметить точку F, в которой восстановить перпендикуляр к диаметру НС. На этом перпендикуляре отметить отрезок
 ;
;из точки Н через точку Fl провести прямую до пересечения с окружностью токов в точке Т, соответствующей скольжению s— ±. Полученная линия НТ является линией электромагнитной мощности (момента);
из точки O1, опустить перпендикуляр на линию НТ и продолжить его до пересечения с окружностью токов в точке Е. Полученная таким образом точка Е соответствует максимальному моменту, так как отрезок ENв масштабе моментов представляет собой максимальный момент двигателя, а отношение отрезков
 — перегрузочную способность двигателя;
— перегрузочную способность двигателя;точка D1на окружности токов соответствует режиму номинальной нагрузки двигателя. Прямоугольный треугольник OD1aпредставляет собой треугольник токов: сторона OD1 — номинальный ток статора (см. п. 4), сторона D1a — активная составляющая тока статора, сторона Оа — реактивная (индуктивная) составляющая тока статора.
для определения коэффициента мощности двигателя сos φ1 сделать дополнительные построения: на оси ординат радиусом 50 мм провести полуокружность, а линию OD1 продолжить до пересечения с этой полуокружностью в точке h. Отношение отрезка Oh к диаметру полуокружности определяет значение коэффициента мощности в режиме номинальной нагрузки:

 ;
;для определения скольжения и частоты вращения ротора двигателя также необходимы дополнительные построения: из точки Н параллельно оси ординат провести линию HQ, затем из точки Qпараллельно линии электромагнитной мощности НТ провести линию до пересечения с продолжением линии полезной мощности НК в точке L. Полученная таким образом линия QL представляет собой шкалу скольжения: в точке холостого хода Н скольжение s = 0, а в точке короткого замыкания К скольжение s= 1. Продолжив отрезок HD1 до пересечения со шкалой скольжения, получится на шкале скольжения точка s1 которая определит скольжение двигателя в режиме номинальной нагрузки, частота вращения при этом равна
 ;
;проверить значение номинальной мощности двигателя по формуле:
 ;
;определить потребляемую в номинальном режиме мощность:
 ;
;определить КПД двигателя в номинальном режиме:
 ;
;определить электромагнитный момент в номинальном режиме:
 .
.
Решить задачу №3. Используя значения параметров трехфазных асинхронных двигателей, приведенные в таблице 8.3 (см. табл. 8.4), рассчитать параметры и построить рабочие характеристики асинхронного двигателя: I1 М2, n2, сos φ1, η= f(Р2). При этом можно воспользоваться либо упрощенной круговой диаграммой, построенной при решении задачи №2, либо применить аналитический метод расчета рабочих характеристик.
Решение аналитическим методом:
определить активную и реактивную составляющие тока холостого хода:
 ;
;определить сопротивление короткого замыкания:
 ;
;определить активную и реактивную составляющие сопротивления короткого замыкания:
 ;
;определить приведенное значение активного сопротивления обмотки ротора:
 ;
;определить критическое скольжение:
 ;
;определить номинальное скольжение sном:
определить величину магнитных потерь:
 ;
;рассчитать значения параметров, приведенных в таблице 8.5. для ряда значений скольжения s = 0,01; 0,02; 0,03; 0,045; 0,06 и для каждого из них выполняем расчет;
результаты представляем в виде таблицы 8.4;
по полученным данным построить рабочие характеристики двигателя (рис. 8. 5).
Таблица 8.3.

Таблица 8.4.
Расчетные формулы
Значения параметра при скольжении s, равном
0,01
0,02
0,03
0,045
0,06

Рисунок 8.5. Рабочие характеристики АД
Таблица 8.5.

Оформить отчет по практической работе.
Ответить на контрольные вопросы.
Сделать вывод о проделанной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
Что представляют собой рабочие характеристики асинхронного двигателя?
Что такое скоростная характеристика асинхронного двигателя?
Как повысить коэффициент мощности асинхронных двигателей?

ПРИЛОЖЕНИЕ









11
Источник
§ 93. ВРАЩАЮЩИЙ МОМЕНТ АСИНХРОННОГО ДВИГАТЕЛЯ
Вращающий момент асинхронного двигателя создается при взаимодействии вращающегося магнитного поля статора с токами в проводниках обмотки ротора. Поэтому вращающий момент зависит как от магнитного потока статора Фт, так и от силы тока в обмотке ротора I2. Однако в создании вращающего момента участвует только активная мощность, потребляемая машиной из сети. Вследствие этого вращающий момент зависит не от силы тока в обмотке ротора I2, а только от его активной составляющей, т. е. I2 cos ψ2, где ψ2 — фазный угол между э. д. с. и током в обмотке ротора.
Таким образом, вращающий момент асинхронного двигателя определяется следующим выражением:
![]()
где С — конструктивная постоянная машины, зависящая от числа ее полюсов и фаз, числа витков обмотки статора, конструктивного выполнения обмотки и принятой системы единиц. При условии постоянства приложенного напряжения магнитный поток остается также почти постоянным при любом изменении нагрузки двигателя.
Таким образом, в выражении вращающего момента величины С и Фт постоянны и вращающий момент пропорционален только активной составляющей тока в обмотке ротора, т. е. ![]()
Изменение нагрузки или тормозного момента на валу двигателя изменяет и скорость вращения ротора и скольжения.
Изменение скольжения вызывает изменение как силы тока в роторе I2, так и ее активной составляющей I2 cos ψ2/
Можно силу тока в роторе определить отношением э. д. с. к полному сопротивлению, т. е.
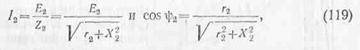
где Z2, r2 и Х2 — полное, активное и реактивное сопротивления фазы обмотки ротора.
Изменение скольжения изменяет частоту тока ротора. При неподвижном роторе (n2=0 и S = 1) вращающееся поле с одинаковой скоростью пересекает проводники обмотки статора и ротора и частота тока в роторе равна частоте тока сети (f2=f1). При уменьшении скольжения обмотка ротора пересекается магнитным полем с меньшей частотой, так что частота тока в роторе уменьшается. Когда ротор вращается синхронно с полем (n2=n1 и S=0), проводники обмотки ротора не пересекаются магнитным полем, так что частота тока в роторе равна нулю f2=0. Таким образом, частота тока в роторе пропорциональна скольжению, т. е. f2=Sf1
Активное сопротивление обмотки ротора почти не зависит от частоты, тогда как э. д.с и реактивное сопротивление пропорциональны частоте, т. е. изменяются с изменением скольжения, и могут быть определены следующими выражениями:
![]()
где Е и X — э. д. с. и индуктивное сопротивление фазы обмотки неподвижного ротора соответственно.
Таким образом, имеем:
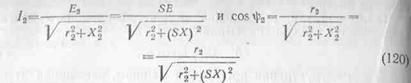
и вращающий момент
![]()
Следовательно, при небольших скольжениях (примерно до 20%), когда SХ мало по сравнению с r2, увеличение скольжения вызывает увеличение вращающего момента, так как при этом воз, растает активная составляющая тока в ротоке (I2соs ψ2). При больших скольжениях (SХ больше, чем r2) увеличение скольжения будет вызывать уменьшение вращающего момента. Таким образом, при больших скольжениях его увеличение хотя и увеличивает силу тока в роторе I2, но ее активная составляющая I2 соs ψ2 и, следовательно, вращающий момент уменьшаются вследствие значительного увеличения реактивного соя противления обмотки ротора.
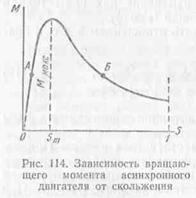
На рис. 114 показана зависимость вращающего момента от скольжения. При некотором скольжении Sт (примерно 20%) двигатель развивает максимальный момент, который определяет перегрузочную способность двигателя и обычно в 2—3 раза превышает номинальный момент.
Устойчивая работа двигателя возможна только на восходящей ветви кривой зависимости момента от скольжения, т. е. при изменении скольжения в пределах от 0 до Sт. Работа двигателя на нисходящей ветви указанной зависимости, т. е. при скольжении S>Sт, невозможна, так как здесь не обеспечивается устойчивое равновесие моментов.
Если предположить, что вращающий момент был равен тормозному (Мвр=Мторм) в точках А и Б, то при случайном нарушении равновесия моментов в одном случае оно восстанавливается, а в другом не восстанавливается. Допустим, что вращающий момент двигателя почему-либо уменьшился (например, при понижений напряжения сети), тогда скольжение начнет увеличиваться. Если равновесие моментов было в точке А, то увеличение скольжения вызовет увеличение вращающего момента двигателя и он станет вновь равным тормозному моменту, т. е. равновесие моментов восстановится. Если же равновесие моментов было в точке Б, то увеличение скольжения вызовет уменьшение вращающего момента, который будет оставаться всегда меньше тормозного, т. е. равновесие моментов не восстановится и скорость вращения ротора будет непрерывно уменьшаться до полной остановки двигателя.
Если приложить к валу двигателя тормозной момент, больший максимального момента, то равновесие моментов не восстановится и ротор двигателя остановится.
 .
.
Вращающий момент двигателя пропорционален квадрату приложенного напряжения, так как пропорциональны напряжению как магнитный поток, так и сила тока в роторе. Поэтому изменение напряжения в сети вызывает значительное изменение вращающего момента.
§ 94. РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ДВИГАТЕЛЯ
Рабочие характеристики асинхронного двигателя представляют собой зависимости скольжения S, числа оборотов ротора n2, развиваемого момента М, потребляемого тока I1, расходуемой мощности Р1, коэффициента мощности соs и к. п. д. η от полезной мощности Р2 на валу машины. Эти характеристики (рис. 115) снимаются три естественных условиях работы двигателя, т. е. двигатель нерегулируемый, частота f1 и напряжение U1 сети остаются постоянными, а изменяется только нагрузка на валу двигателя.
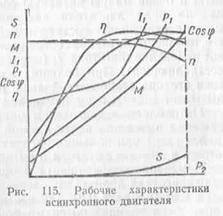
При увеличении нагрузки на валу двигателя скольжение возрастет, причем при больших нагрузках скольжение увеличивается несколько быстрее, чем при малых.
При холостом ходе двигателя п2=n1 или S=0.
При номинальной нагрузке скольжение обычно составляет S = 3-5%.
Скорость вращения ротора
![]()
Так как при увеличении нагрузки на валу двигателя скольжение возрастает, то число оборотов будет уменьшаться. Однако изменение скорости вращения при увеличении нагрузки от 0 до номинальной очень незначительно и не превышает 5%. Поэтому скоростная характеристика асинхронного двигателя является жесткой — она имеет очень малый наклон к горизонтальной оси.
Вращающий момент, развиваемый двигателем М, уравновешен тормозным моментом на валу М2 и моментом, идущим на преодоление механических потерь М0, т. е.
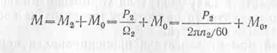
где Р2 — полезная мощность двигателя,
2 — угловая скорость ротора.
При холостом ходе двигателя вращающий момент равен М0; с увеличением нагрузки на валу этот момент также увеличивается, причем за счет некоторого уменьшения скорости ротора увеличение вращающего момента происходит быстрее, чем увеличение полезной мощности на валу.
Источник

