Примеры полезной и не полезной инерции
Каждый день мы сталкиваемся с явлением инерции. Имея различное высокотехнологичное оборудование, человечество так и не научилось преодолевать хотя бы на малую величину, влияние инерции. В данной статье анализируются гипотезы о возможном преодолении, ликвидации инерции, а также о ее природе.
Сначала подберемся к понятию инерции: инерция — это свойство, которое проявляет масса, пытаясь сохранить свое состояние движения при ускорениях и смене направления движения (как в случае с центробежной силой). Причем инерционность тела растет не только при увеличении массы, но и при увеличении протяженности тела в пространстве, вспомним формулы момента инерции:
Из формулы видно, что, к примеру, для диска, инерционность диска будет увеличиваться с увеличением как массы m, так и его радиуса R. Если говорить проще, то цилиндр, массой 10000 кг и радиусом 1 метр, будет трудно раскрутить и остановить так же как диск массой 1 кг и радиусом 100 метров.
Существуют различные мнения об природе инерции, которые местами противоречат друг другу. Известен парадокс Маха, в котором утверждается, что инерция (центробежная сила) никогда не будет проявляться для вращающегося тела, если не будет других тел во Вселенной, кроме как этого вращающегося тела. Реальность такого парадокса поддерживается теорией относительности А. Эйнштейна. Также эта теория утверждает, что инерционность одной массы будет зависеть от расстояния до других масс, и чем это расстояние больше, тем меньше будет инерция тела удаленного от других масс (цитата: «Поэтому если я удалю какую-нибудь массу на достаточно большое расстояние от всех других масс Вселенной, то инерция этой массы должна стремиться к нулю.» стр. 605 «Вопросы космологии и общая теория относительности.» А. Эйнштейн Собрание научных трудов. — М.: Наука, 1965. — Т. 1). Но неизвестны такие опытные данные, которые согласовались бы с этой точкой зрения, также не представляется осуществимым на опыте реализации, парадокса Маха, одиноко вращающегося тела во Вселенной. Существуют точки зрения, что сил инерции вообще не существуют, и это математическая фикция, у нас в стране это известно под спором академиков А.Ю. Ишлинского и Л.И. Седова (на фотографии ниже, как раз они, статьи затрагивающие этот спор: тут и тут).
Споры происходили и в более поздние времена, известна дискуссия на эту тему в советских научно-технических изданиях Л.Г. Ливенсона и Г.К. Суслова в 1936-1937 годах.
Одним из примеров о разном понимании фиктивности или реальности сил инерции могут послужить эти две цитаты известных ученых:
А.Н. Матвеев «Механика и теория относительности» 1976 г.:
«Являются ли силы инерции реальными силами? Они реальны в том же смысле, в каком являются реальными ускорения, для описания которых они введены. Они реальны также и в более глубоком смысле: при рассмотрении физических явлений можно указать конкретные физические последствия действия сил инерции. Например, в вагоне поезда силы инерции могут привести к увечьям пассажиров, т.е. к весьма реальному и осязаемому результату».
Н.В.Гулиа «Инерция» 1982 г.:
«Все силы инерции – силы нереальные, необходимые нам лишь для облегчения тех или иных задач механики. Ни в коем случае нельзя их считать реальными силами и приписывать им свойства и действия физических сил».
Также похожие споры встречаются и в современности, подобное столкновение, двух точек зрения о фиктивности или реальности сил инерции представлены в теме этого физического форума. И тем не менее, даже среди тех кто выступает за реальность силы инерции и толкования её физической причины — нет общего согласия. Однако, есть общие точки соприкосновения, она гласит, что инерция тела вызывается физической средой, которая существует во всем материальном пространстве, которая сопротивляется ускорению и смене направления движущейся массы.
Одна из них утверждает, что такая среда, которая ответственна не только за инерцию, но и из-за распространения света, должна иметь собственную массу, то есть это среда упругая, по типу некоторых эфирных гипотез 19-20 веков, примером такого представления может служить воззрения, известного теоретика массового эфира В.А. Ацюковского, в своей работе (Эфиродинамические основы электромагнетизма, стр. 21) он выводит примерную массу частички элемента эфира «амера» как кг, количество таких частичек-амеров в кубометре пространства выводит . Резюмирую такие рассуждения можно сказать что подход массового эфира не раскрывает причину наблюдения инерции у массы, объявляя саму причину массой, даже если очень маленькой. То есть даже если принять что инерция у нас возникает из-за амеров, то возникает вопрос по каким причинам происходит инерция у самих амеров раз у них тоже есть масса и они могут вращаться (образуя вихри) и соударяться друг о друга? Также это рождает и другие парадоксы и несоответствия опытным данным. К примеру, известный опыт Майкельсона, по обнаружению ветра такой массовой всепроницающей среды, ветер не был обнаружен. Еще в качестве примера одного из них, можно привести формулы моментов для центрифуг при вентиляционных потерях из-за сопротивления упругой среды (статический момент) и при динамическом (инерционном) моменте.
Статический момент, сопротивление движению упругой (массовой) среды+механические потери, вычисляется по формуле:
— коэффициент вентиляционных потерь, зависит от плотности среды
— момент трения в подшипниках
— угловая скорость
Динамический (инерционный) момент рассчитывается по формуле:
где — момент инерции
— угловая скорость
— время разгона
Из формул видим, что природа сопротивления упругой среды, имеет другую природу, нежели чем получаем при ускорениях. Упругая среда сопротивляется квадратично, в зависимости от скорости вращения, то есть чем больше скорость, тем больше сопротивляется «инерция» если брать упруго-эфирную точку зрения, но никакой квадратичной зависимости от скорости вращения не наблюдается для тел где наблюдается инерция. То есть получаем, что гипотеза упругого эфира не способна объяснять такое явление как инерция. Тем не менее В.А. Ацюковский предлагает способы по уменьшению инерции если ускоряющиеся тела «продувать эфиром«, такой продув автор предлагает делать «с помощью аннигиляции эфирных вихрей«, но не встречено объяснение как создать такие вихри.
Другая точка зрения, которая также поддерживает мысль о причине инерции, как проявлении всепроницаемой, но именно безмассовой среды, это структура вакуума А.В. Рыкова (из ОИФЗ РАН). Гипотеза спорная, хоть и не противоречит известному опыту Майкельсона и другим опытам, в которых упругий, массовый эфир вызывает несоответствия опытным данным. Гипотеза получила положительные рецензии, академика РАН д.ф-м.н. В.Н. Страхова (прочитать его рецензию можно тут) и к.ф-м.н. вед. науч. сотрудника РНЦ «Курчатовский институт», одного из разработчиков самой мощной взорванной бомбы в истории человечества Царь-бомбы, Ю.Н. Смирнова (с ним удалось поговорить лично, прочитать его рецензию можно тут). Гипотеза выведена на основании факта рождения пар масс элементарных частиц при гамма-излучении в вакууме вблизи атома ядра или частицы, то есть все массы рождаются из этой среды при определенной энергии от 1,022 МэВ и выше, а также факта токов смещения в вакууме, наличия одного заряда ( Кл) для всех элементарных частиц независимо от массы.
Если коротко, среда состоит из электрических безмассовых зарядов «+» и «-» и магнитного потока между ними. При движении, известные массовые частицы и античастицы двигаются по этим зарядам, приобретая тем самым волнообразное движение, длина волны которых считается по формуле де Бройля:
Магнитный поток сопротивляется ускорению частиц и смене направления движения частиц, не дает сразу перепрыгнуть частицам с одной амплитуды движения в зарядовой решетке на другую или сделать моментально поворот в этой решетке.
Автор теории отрицает кварки (кстати, кварки так и не получены в свободном состоянии) считает нейтрон состоящим из электрона и протона. Нейтрино, считает безмассовым своеобразным магнитоэлектрическим излучением (не электромагнитным) частота которого превышает Гц, высчитывает скорость гравитации выше скорости света в 3576,055 раз, не считает что в черной дыре встает время, а нераспространение в ней света, трактует как отсутствие среды для него, по аналогии как вакуум не имеет среды для распространения звука. За кварки, нейтрино и расчет скорости гравитации с помощью усовершенствованных установок Майкельсона, которая в этих расчетах равна скорости света (достоверность этого опыта вызывает споры в научном сообществе) получены Нобелевские премии.
Гипотеза Рыкова предлагает идеи о преодолении инерции, гипотетически, гамма-излучение деформирует среду отвечающую за инерцию и уменьшает ее величину. Видео представляет упрощенно такой опыт:
Упрощенное видео, является вольной трактовкой идей автора по прочитанному в его книге, видео делалось без согласования с автором, пока писалась статья автор гипотезы умер.
Немного пояснений к видео: вокруг тела, на котором мы наблюдаем в обычных условиях явление инерции, создан «кокон» из гамма-лучей некой энергии, автор указывал на вероятность наблюдения эффекта уменьшения величины инерции от выбора частоты гамма-излучения. Также высказана гипотеза об уменьшении инерции с помощью переменного магнитного поля и вращательных ускорений.
Более подробное описание с формулами у автора таких предположений в его книге «Вакуум и вещество Вселенной», глава «Возможные практические технологии», стр. 136.
Вдобавок по теме
Мной был сделан фильм в котором рассматривается гипотеза Рыкова о строении среды Вселенной и история взглядов на такой вопрос, в 2011 году, на киностудии Леннаучфильм.
О фильме, как вопиющем примере псевдонауки, писала Газета.ру, однако, при этом серьезно переврав об утверждениях сделанных в фильме:
1) Неверно указано представление Анатолия Рыкова о структуре вакуума:
«структура вакуума представляет собой кристаллическую решетку из элементарных частиц, связанных между собой силами электричества».
В фильме говорится что структура вакуума наоборот безмассовая и это очень важная черта этой теории.
2) Неверно представлена информация данная в фильме:
«векторы электрических и магнитных полей («магнитные» потоки) в кристалле вакуума были параллельны, а не перпендикулярны друг другу».
Про это вообще не говорится и не показывается в фильме.
3) «Фильм «Структура вакуума»… вызвавших массу гневных откликов в научном сообществе» — не совсем так, часть научного сообщества одобрительно отозвалась о фильме, а часть научного сообщества была «гневной».
4) Искажена степень наук ученого чья гипотеза рассматривается в фильме: «Этот двадцатиминутный ролик был посвящен гипотезе кандидата наук из Института физики Земли».
Кандидата физико-математических наук правильно.
После резонанса в СМИ, я стал лауреатом молодежной премии правительства Санкт-Петербурга за научно-популярное кино.
Нельзя здесь обойти популярное поле Хиггса. Согласно этой гипотезе, существует всепроницающее вакуумное поле Хиггса, и при ускорениях масс — это поле создает инерцию массы. Более подробно про эту гипотезу можно почитать тут, тут (статьи И.П. Иванова) и тут (статья Э.Э. Бооса и др.). Гипотеза Питера Хиггса, о всепроницающем поле, которое порождает инерцию, напоминает высказывание Анри Пуанкаре: «Инерцией обладает не материя, а эфир; он один оказывает сопротивление движению». Только «эфир» Хиггса не является светоносным. В гипотезе Хиггса, не встречено, как это поле воздействует на массу
при смене направления движения
, когда тоже проявляется инерция. Также не встречено гипотез согласующихся с механизмом Хиггса, о возможности преодоления инерции.
Достаточно широко встречаются также и различные полумистические описания, о летающей тарелке преодолевающей инерционное сопротивление на якобы тайных знаниях Тесла, но в этих писаниях на мой взгляд почти рандомно перебираются различные физические термины, то есть крайне некорректно.
Также встречаются статьи в различных источниках, и даже в серьезных изданиях типа письма в ЖТФ, в которых утверждается, что создана установка (к примеру установки: Дж. Серла, В.С. Гребенникова, В.В. Рощина и С.М. Година) на которой испытатели достигли небывалых эффектов в уменьшении инерции/гравитации/веса, но потом по каким-то причинам установка утрачена, новую, повторяющую достигнутые эффекты, почему-то не удается/не удалось сделать, свидетелей таких небывалых эффектов единицы, а документальные доказательства выглядят малоубедительно, что наводит подозрения о блефе.
Возможность преодоления инерции важна для осуществления старинных мечтаний человечества о межзвездных путешествиях, то что даже если человечество научится получать большие скорости перемещения, то одним из негативных факторов сдерживающий такие перемещения, могут стать очень сильные перегрузки, возникающие по причине инерции, которые воздействуют на материал космического корабля и его пассажиров.
Ресурсы с которых были использованы изображения:
1. Объясните назначение ремней безопасности в автомобиле
2. Момент инерции
3. Александр Юльевич Ишлинский
Источник
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).
В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:
а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:
- внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;
- внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);
б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):
- движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;
- сила сопротивления препятствует движению звена и развивает отрицательную мощность.
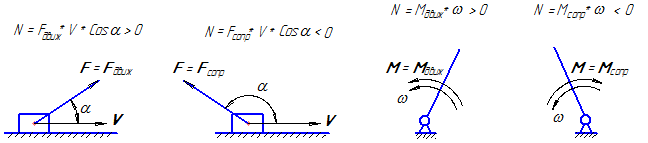
Рисунок 16
В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:
- силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);
- силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений.
Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;
в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;
г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;
д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:
Fин=-m∙as
Mин=-Is∙e
где
Fин – главный вектор сил инерции, приложенный в центре масс звена;
Mин – главный момент сил инерции;
m – масса звена;
Is – момент инерции звена относительно центра масс;
as – ускорение центра масс звена;
e – угловое ускорение звена.
Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.
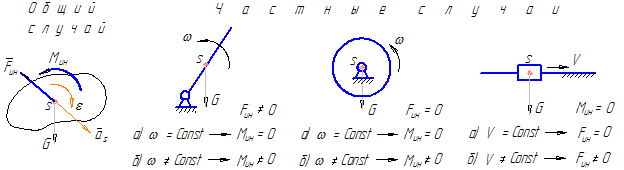
Рисунок 17
При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.
Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.
Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).
Поэтому для решения поставленной задачи применяется метод кинетостатики.
Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.
Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.
Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.
Условие статической определимости плоской кинематической цепи:
Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется «n» подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.
На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.
В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.
При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.
Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).
Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).
Если в кинематической цепи количество пар пятого класса равно Р5, то на определение реакций во всех этих парах надо затратить 2Р5 уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р4.
Таким образом, из 3n независимых уравнений статики 2Р5 уравнений используются для определения реакций в парах пятого класса и Р4 – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.
Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда
X=3n–2Р5–Р4,
но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.
Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы.
Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:
- разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;
- решение начинают с последней присоединенной группы и заканчивают начальным звеном.
При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.
Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.
Кинетостатика групп Ассура второго класса >
Курсовой проект по ТММ >
Источник

