Работа и коэффициент полезного действия цикла
В термодинамике цикл Карно́ или процесс Карно — это идеальный[1]круговой процесс, состоящий из двух адиабатных и двух изотермических процессов[2]. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[3].
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[4][5].
Поскольку идеальные процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности.
Коэффициент полезного действия (КПД) любой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника[6]. По этой причине, позволяя оценить верхний предел КПД тепловой машины, цикл Карно важен для теории тепловых машин. В то же время КПД цикла Карно настолько чувствителен к отклонениям от идеальности (потерям на трение), что данный цикл никогда не применяли в реальных тепловых машинах[K 1][8].
Описание цикла Карно[править | править код]
Рис. 1. Цикл Карно в координатах T—S
Рис. 2. Цикл Карно в координатах p—V
Рис. 3. Цикл Карно на термодинамической поверхности идеального газа
Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах (температура) и (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→B). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты , то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 — процесс B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс C→D). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс D→A). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Обратный цикл Карно[править | править код]
В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[9][10]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс В→Б); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс Б→А); адиабатического расширения (на рис. 1 — процесс А→Г); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс Г→В).
КПД тепловой машины Карно[править | править код]
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Первая и вторая теоремы Карно[править | править код]
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[11]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[12][13]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
Связь между обратимостью цикла и КПД[править | править код]
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[14]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например цикл Эрикссона (англ.)русск., состоящий из двух изобар и двух изотерм[14].
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
См. также[править | править код]
- Термодинамические циклы
- Первое начало термодинамики
- Второе начало термодинамики
- Термодинамическая энтропия
- Термодинамические потенциалы
Комментарии[править | править код]
- ↑ В реальных тепловых машинах цикл Карно не используют, поскольку практически невозможно осуществить процессы изотермического сжатия и расширения. Кроме того, полезная работа цикла, представляющая собой алгебраическую сумму работ во всех четырех составляющих цикл частных процессах, даже в идеальном случае полного отсутствия потерь мала по сравнению с работой в каждом из частных процессов, то есть мы имеем дело с обычной ситуацией, когда итоговый результат представляет собой малую разность больших величин. Применительно к математическим вычислениям это означает высокую отзывчивость результата даже на небольшие вариации значений исходных величин, а в рассматриваемом нами случае соответствует высокой чувствительности полезной работы цикла Карно и его КПД к отклонениям от идеальности (потерям на трение). Эта связь с отклонениями от идеальности настолько велика, что с учетом всех потерь полезная работа цикла Карно приближается к нулю[7].
Примечания[править | править код]
- ↑ То есть без потерь, в первую очередь на трение.
- ↑ Карно цикл // Италия — Кваркуш. — М. : Советская энциклопедия, 1973. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 11).
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 94.
- ↑ Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
- ↑ Второе начало термодинамики. (Работы Сади Карно — В. Томсон — Кельвин — Р. Клаузиус — Л. Больцман — М. Смолуховский) / Под. ред. А. К. Тимирязева. — Москва—Ленинград: Государственное технико-теоретическое издательство, 1934. — С. 17—61.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113—114.
- ↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 112.
- ↑ Кинан Дж., Термодинамика, 1963, с. 93.
- ↑ Николаев Г. П., Лойко А. Э., Техническая термодинамика, 2013, с. 172.
- ↑ Бахшиева Л. Т. и др., Техническая термодинамика и теплотехника, 2008, с. 148.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 95.
- ↑ Сивухин, Т. II. Термодинамика и молекулярная физика, 2005, с. 113.
- ↑ Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 35.
- ↑ 1 2 Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.
Литература[править | править код]
- Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. — Paris: Gauthier-Villars, Imprimeur-Libraire, 1878. — 102 p. (фр.)
- Бахшиева Л. Т., Кондауров Б. П., Захарова А. А., Салтыкова В. С. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М.: Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1.
- Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с. (недоступная ссылка)
- Кинан Дж. Термодинамика / Пер с англ. А. Ф. Котина под ред. М. П. Вукаловича. — М.—Л.: Госэнергоиздат, 1963. — 280 с.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V).
- Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
- Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.
Источник
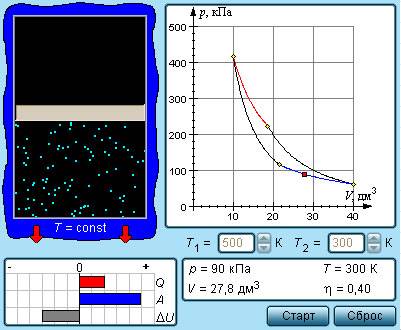
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Определение 1
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0):
A=Q
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.1 в виде диаграммы (p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1, эквивалентную площади под кривой abc. При сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A=A1+A2 на диаграмме (p, V) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.
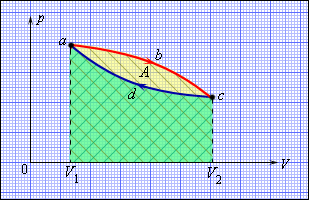
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd.
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Определение 2
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q=Q1+Q2=Q1-Q2.
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0. Основываясь на первом законе термодинамики, запишем:
∆U=Q-A=0.
Из этого следует:
A=Q=Q1-Q2.
Работа A, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q.
Определение 3
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q1, то есть:
η=AQ1=Q1-Q2Q1.
Рисунок 3.11.2. Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1. На рисунке 3.11.3 проиллюстрирована энергетическая схема тепловой машины.
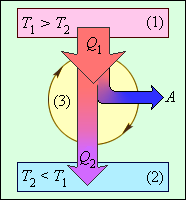
Рисунок 3.11.3. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2.
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4) и две адиабаты (2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4), одну изобару (2–3) и одну изохору (4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %, у дизельного двигателя – приблизительно 40 %.
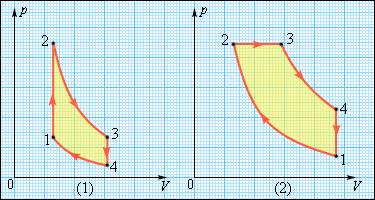
Рисунок 3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2).
Цикл Карно
Круговой процесс, изображенный на рисунке 3.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.
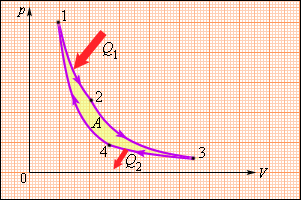
Рисунок 3.11.5. Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12количество теплоты Q1=A12. После этого на участке адиабаты (2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0. Его температура при адиабатическом расширении снижается до величины T2. На идущем следующим участке изотермы (3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0 и отдается тепло Q2<0, эквивалентное произведенной им работе A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1, также совершается работа A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A=A12+A23+A34+A41.
На диаграмме (p, V) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–2 и 3–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔU его внутренней энергии. Для 1 моля газа верно следующее выражение:
A=-∆U=-CV(T2-T1),
в котором T1 и T2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
A23=-A41.
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2и нагревателя T1:
η=T1-T2T1=1-T2T1.
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
ηКарно=ηmax

Рисунок 3.11.6. Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Определение 4
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V) обходятся против часовой стрелки. На рисунке 3.11.7 проиллюстрирована энергетическая схема холодильной машины.
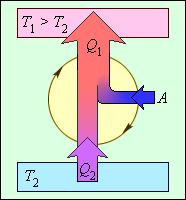
Рисунок 3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2.
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Определение 5
Если полезным эффектом является отбор некоторого количества тепла Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
βx=Q2A.
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. В условиях подобного определения βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
βx=T2T1-T2.
Определение 6
В случае, когда полезным эффектом является передача некоего количества тепла
|Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность βТ теплового насоса может быть определена с помощью отношения:
βт=Q1A.
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
Q1>A.
Следовательно, βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
βт=1η=T1T1-T2.
Источник

