Зависимость полезной мощности от силы тока в цепи
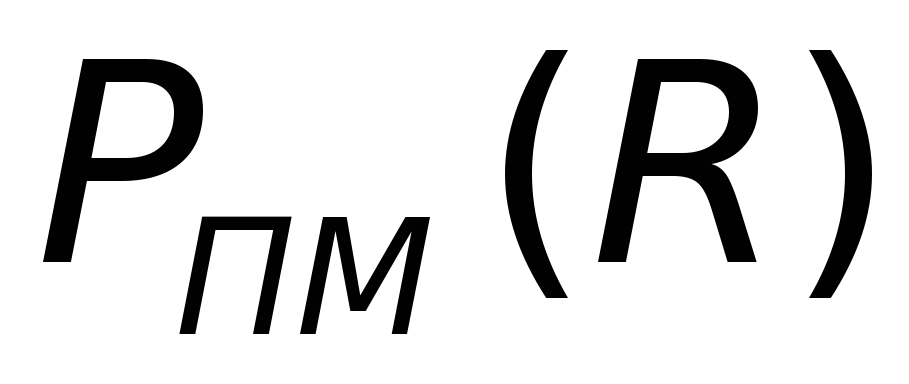
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
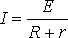, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
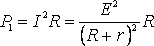. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®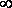
эта мощность равна нулю. При всех других конечных значениях Rмощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
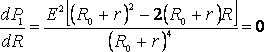. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи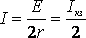 
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
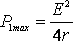. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
. 
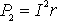(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
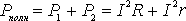= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен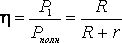 
. (9)
Из формулы (8) следует, что
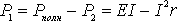, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при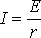 
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
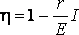(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
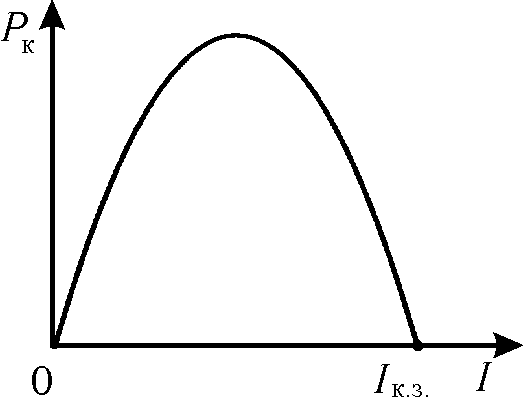
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.
Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ
Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой 
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку 
в нижней части экрана) и амперметр (кнопка 
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр 
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода 
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой 
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Е, В | 10,0 | 9,5 | 9,0 | 8,5 | 8,0 | 8,5 | 9,0 | 9,5 |
r, Ом | 4,8 | 5,7 | 6,6 | 7,5 | 6,4 | 7,3 | 8,2 | 9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
R, Ом | 2,0 | 2,5 | 3,0 | … | 20 |
U, В | |||||
I, А | |||||
P1, Вт | |||||
P2, ВТ | |||||
Pполн, ВТ | |||||
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
Источник
Рассмотрим
электрическую цепь, состоящую из
источника постоянного тока и внешнего
сопротивления R
(рис. 1). При протекании тока через
такую цепь источником ЭДС выполняется
работа и в цепи выделяется мощность.
П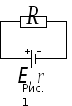
олезной
мощностью называют
мощность, которая выделяется на внешнем
сопротивлении. Из закона Джоуля-Ленца
(10*) полезная
мощность равняется
,
а из закона Ома для участка цепи
.
Тогда полезная мощность будет
| (1) |
, где
– падение напряжения на внешнем
сопротивлении. При протекании тока по
цепи также выделяется „бесполезная”
мощность – разогревается источник ЭДС.
По закону Джоуля-Ленца эта мощность
равняется
.
Полная мощность, которая выделяется во
всей цепи, равняется
.
Используя закон Ома для полной цепи
,
можно найти полную мощность
| (2) |
.И
так,
полная мощность, которая выделяется в
цепи, равняется произведению силы тока
на ЭДС источника тока.
Пусть
в цепи можно менять внешнее сопротивление
.
Проанализируем, как полезная и полная
мощности зависят от силы тока и внешнего
сопротивления.
Полезная
мощность
равняется разности между полной мощностью
и „бесполезной”:
| (3) |
. 
Рис. 2
Из этого
выражения видно, что полезная мощность
является квадратичной функцией силы
тока I.
График этой функции будет представлять
собой параболу (рис. 2).
Из рис. 2
вытекает, что
в двух случаях:
когда
цепь разомкнута (R = ∞),
то сила тока в цепи I = 0;когда
возникло короткое заключение, при этом
R = 0,
а сила тока в цепи будет максимальной
.
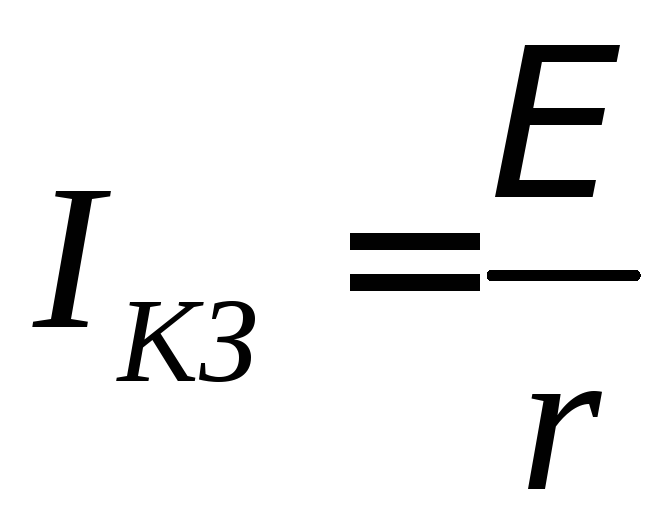Меняя
величину внешнего сопротивления, можно
достичь некоторого значения силы тока
в цепи, при котором полезная мощность
будет максимальной. Найдем этот ток.
Для этого найдем первую производную
и приравняем ее нулю. Из выражения (3)
имеем:
| (4) |
. Отсюда
вытекает
| (5) |
, а ток
,
при котором выделяется максимальная
полезная мощность, равняется
.
С другой стороны, на основании закона
Ома для полной цепи
,
где
– сопротивление, при котором выделяется
максимальная полезная мощность.
Приравнивая два последних выражения
,
находим, что
| (6) |
. Таким
образом, полезная
мощность будет максимальной при условии
равенства внешнего и внутреннего
сопротивлений.
Зависимость
полезной мощности от внешнего сопротивления
можно найти из закона
Джоуля-Ленца
и закона Ома для полной цепи
| (7) |
. График
зависимости
показан на рис. 3 (криваяб).
Максимум функции
можно найти, приравнивая
нулю
| (8) |
.Из
(8) также вытекает ожидаемое равенство
.
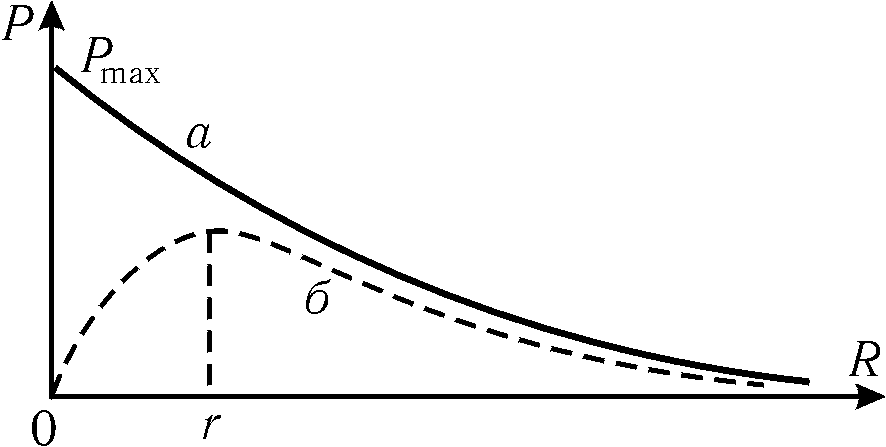
а
– полная мощность
б
– корисна потужність
Рис.
3
Рассмотрим
теперь, как полная мощность
зависит от внешнего сопротивления.
Используя выражение (2) и закон Ома для
полной цепи
находим зависимость полной мощности
от внешнего сопротивления:
.
(9)
График этой
зависимости показана на рис. 3 (кривая
а). При
изменении внешнего сопротивления от
нуля (короткое заключение) до бесконечности
(цепь разомкнута) полная мощность будет
убывать от максимального значения
до нуля.
Зависимость
коэффициента полезного действия
источника электрического тока от силы
тока и внешнего сопротивления цепи
К
оэффициент
полезного действия
(КПД) равняется отношению полезной
мощности (1) к полной мощности (2), которая
выделяется во всей цепи
| (10) |
С
начала
найдем зависимость КПД
от силы тока. Если
разделить выражение (3) для полезной
мощности на выражение (1) для полной
мощности, получим
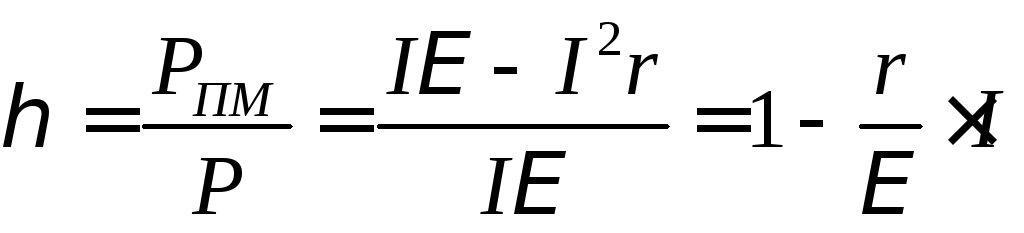
(11)
И
так,
КПД представляет собой линейную функцию
от силы тока (рис. 4). Когда I → 0
(цепь разомкнут), то
.
При коротком заключении
,
ток короткого заключения
| (12) |
и
КПД будет
.
Чтобы найти
зависимость КПД от
внешнего сопротивления,
подставим в (9) выражение для
из закона Ома для участки цепи
,
а выражение для
– из закона Ома для полной цепи
.
Тогда
| (13) |
. Из соотношения (13)
вытекает:
при
R® 0
(короткое заключение,
)
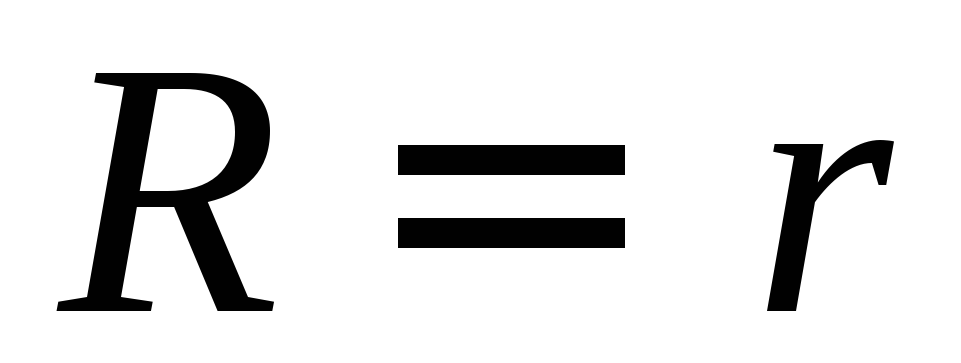;при
R® ¥
( цепь разомкнут,
)
;при
R = r
(условие максимума полезной мощности)
.
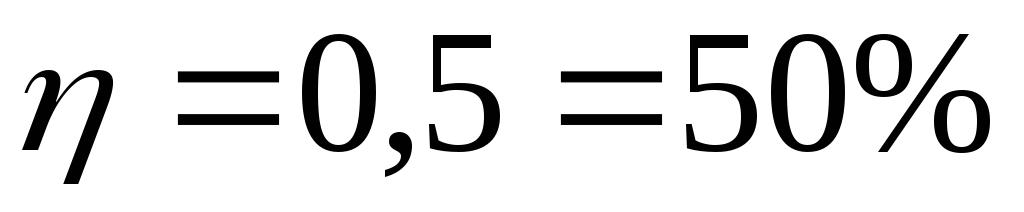Приведенный
анализ показывает, что при увеличении
внешнего сопротивления КПД асимптотично
приближается к единице (рис. 5).
Соседние файлы в папке doc-формат
- #
- #
- #
- #
- #
- #
Источник
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
Источник
Мощность технического оборудования или энергетических установок (аппаратов, агрегатов), отдаваемая ими для совершения работы, указана в их технических характеристиках. Но это не значит, что вся она используется по прямому назначению для достижения результата. Только полезная мощность расходуется на выполнение работы.
Общее определение мощности
Определение и формула полезной мощности
Стоит рассмотреть понятие полезной мощности и формулу на примере электрической цепи. Та мощность, которую источник питания (ИП), в частности, тока, развивает в замкнутой цепи, будет полной мощностью.
Схема цепи
Цепь включает в себя: источник тока, имеющий ЭДС (E), внешнюю цепь с нагрузкой R и внутреннюю цепь ИП, сопротивление которого R0. Формула полной (общей) мощности равна:
Pобщ = E*I.
Здесь I – это значение тока, проходящего по цепи (А), а E – величина ЭДС (В).
Внимание! Падение напряжения на каждом из участков будет равно U и U0, соответственно.
Значит, формула примет вид:
Pобщ = E*I = (U + U0) *I = U*I + U0*I.
Видно, что значение произведения U*I равняется мощности, отдаваемой источником на нагрузке, и соответствует полезной мощности Pпол.
Величина, равная произведению U0*I, соответствует мощности, которая теряется внутри ИП на нагрев и преодоление внутреннего сопротивления R0. Это мощность потерь P0.
Подставляемые в формулу значения показывают, что сумма полезной и потерянной мощностей составляют общую мощность ИП:
Pобщ=Pпол+P0.
Важно! При работе любого аппарата (механического или электрического) полезной мощностью будет та, которая останется для совершения нужной работы после преодоления факторов, вызывающих потери (нагрев, трение, противодействующие силы).
Параметры источника питания
На практике часто приходится думать, какой должна быть мощность источника тока, сколько нужно ватт (вт) или киловатт (квт) для обеспечения бесперебойной работы устройства. Для понимания сути нужно иметь представления о таких понятиях, применяемых в физике, как:
- полная энергия цепи;
- ЭДС и напряжение;
- внутреннее сопротивление источника питания;
- потери внутри ИП;
- полезная мощность.
Независимо от того, какую энергию выдаёт источник (механическую, электрическую, тепловую), мощность его должна подбираться с небольшим запасом (5-10%).
Полная энергия цепи
При включении в цепь нагрузки, которая будет потреблять энергию от источника тока (ИТ), ток будет совершать работу. Энергия, выделяемая на всех включенных в цепь потребителях и элементах цепи (провода, электронные компоненты т.д.), носит название полной. Источник энергии может быть любой: генератор, аккумулятор, тепловой котёл. Цифра значения полной энергии будет складываться из энергии, затрачиваемой источником на потери, и количества, затрачиваемого на выполнение конкретной работы.
ЭДС и напряжение
В чём разница между этими двумя понятиями?
ЭДС – электродвижущая сила, это напряжение, которое сторонние силы (химическая реакция, электромагнитная индукция) создают внутри источника тока (ИТ). ЭДС – это сила перемещения электрических зарядов в ИТ.
ЭДС определение
К сведению. Измерить значение E (ЭДС) представляется возможным только в режиме холостого хода (х.х.). Подключение любой нагрузки вызывает потерю напряжения внутри ИП.
Напряжение (U) – физическая величина, представляющая собой разность потенциалов ϕ1 и ϕ2 на выходе источника напряжения (ИН).
Разность потенциалов
Полезная мощность
Определение понятия полной мощности применяют не только в отношении электрических цепей. Оно применимо и по отношению к электродвигателям, трансформаторам и прочим устройствам, способным потреблять, как активную, так и реактивную составляющую энергии.
Потери внутри источника питания
Подобные потери происходят на внутреннем сопротивлении двухполюсника. У аккумулятора это сопротивление электролита, у генератора – обмоточное сопротивление, провода выводов которого выходят из корпуса.
Внутреннее сопротивление источника питания
Взять и просто измерить R0 тестером не получится, узнать его обязательно нужно для вычисления потерь Р0. Поэтому применяют косвенные методы.
Косвенный метод определения R0 заключается в следующем:
- в режиме х.х. замеряют E (В);
- при включенной нагрузке Rн (Ом) измеряют Uвых (В) и ток I (А);
- падение напряжения внутри источника считают по формуле:
U0=E-Uвых.
На последнем этапе находят R0=U0/I.
Схема для измерения R0
Взаимосвязь полезной мощности и КПД
Коэффициент полезного действия (КПД) – величина безразмерная, численно выражается в процентах. КПД обозначают буквой η.
Формула имеет вид:
η = А/Q,
где:
- А – полезная работа (энергия);
- Q – затраченная энергия.
По мере увеличения КПД в различных двигателях допустимо выстроить следующую линейку:
- электродвигатель – до 98%;
- ДВС – до 40%;
- паровая турбина – до 30%.
Что касается мощности, КПД равен отношению полезной мощности к полной мощности, которую выдает источник. В любом случае η ≤ 1.
Важно! КПД и Pпол не одно и то же. В разных рабочих процессах добиваются максимума или одного, или другого.
Получение максимальной энергии на выходе ИП
К сведению. Чтобы увеличить КПД подъёмных кранов, нагнетательных насосов или двигателей самолётов, нужно уменьшить силы трения механизмов или сопротивления воздуха. Этого достигают применением разнообразных смазок, установкой подшипников повышенного класса (заменив скольжение качением), изменением геометрии крыла и т.д.
Максимальная энергия или мощность на выходе ИП может быть достигнута при согласовании сопротивления нагрузки Rн и внутреннего сопротивления R0 ИП. Это значит, что Rн = R0. В этом случае КПД равен 50%. Это вполне приемлемо для малоточных цепей и радиотехнических устройств.
Однако этот вариант не подходит для электрических установок. Чтобы впустую не тратились большие мощности, режим эксплуатации генераторов, выпрямителей, трансформировав и электродвигателей таков, что к.п.д. приближается к 95% и выше.
График зависимости Рпол и η от тока в цепи
Достижение максимального КПД
Формула КПД источника тока имеет вид:
η = Pн/Pобщ = R/Rн+r,
где:
- Pн – мощность нагрузки;
- Pобщ – общая мощность;
- R – полное сопротивление цепи;
- Rн – сопротивление нагрузки;
- r – внутреннее сопротивление ИТ.
Как видно из графика, изображённого на рис. выше, мощность Pн с уменьшением тока в цепи стремится к нулю. КПД, в свою очередь, достигнет максимального значения, когда цепь будет разомкнута, и ток равен нулю, при коротком замыкании в цепи станет равным нулю.
Если обратиться к элементарному тепловому двигателю, состоящему из поршня и цилиндра, то у него степень сжатия равна степени расширения. Повышение КПД такого мотора возможно в случае:
- изначально высоких параметров: давления и температуры рабочего тела перед началом расширения;
- приближения их значений к параметрам окружающей среды по окончании расширения.
Достижение ηmax доступно лишь при наиболее эффективном изменении давления рабочего компонента во вращательное движение вала.
К сведению. Термический коэффициент полезного действия повышается с повышением доли теплоты, подаваемой к рабочему телу, которая преобразуется в работу. Подаваемая теплота делится на два вида энергии: внутренняя в виде температуры и энергия давления.
Механическую работу, по сути, совершает только второй вид энергии. Это порождает целый ряд минусов тормозящих процесс повышения КПД:
- некоторая часть давления уходит на внешнюю среду;
- достижение максимального коэффициента полезного действия невозможно без увеличения процента использования энергии давления для преобразования в работу;
- нельзя поднять КПД тепловых двигателей, не изменяя S поверхности приложения давления, и без удаления этой поверхности от точки вращения;
- использование только газообразного рабочего тела не способствует повышению η тепловых двигателей.
Для достижения высокого коэффициента полезного действия теплового двигателя нужно определяться с рядом решений. Этому способствуют следующие модели устройства:
- ввести в цикл расширения ещё одно рабочее тело с другими физическими свойствами;
- наиболее полно перед расширением использовать оба вида энергии рабочего тела;
- осуществлять генерацию добавочного рабочего тела прямо при расширении газообразного.
Информация. Все доработки двигателей внутреннего сгорания в виде: нагнетателя турбонадува, организации многократного или распределённого впрыска, а также повышения влажности воздуха, доведения топлива при впрыске до состояния пара, не дали ощутимых результатов резкого повышения КПД.
КПД двигателя внутреннего сгорания
Коэффициент полезного действия нагрузки
Какой бы ни была мощность источника, кпд электроприборов никогда не будет равна 100%.
Исключение. Принцип теплового насоса, применяемый в работе холодильников и кондиционеров, приближает их КПД к 100%. Там нагрев одного радиатора приводит к охлаждению другого.
В остальном случае энергия уходит на посторонние эффекты. Чтобы уменьшить этот расход, нужно обращать внимание на сопутствующие факторы:
- при обустройстве освещения – на конструкцию светильников, устройство отражателей и цвет окраски помещений (отражающий или светопоглощающий);
- при организации отопления – на теплоизоляцию тепловодов, установку рекуперационных вытяжных устройств, утепление стен, потолка и пола, монтаж качественных оконных стеклопакетов;
- при организации электропроводки – правильно подбирать марку и сечение проводников соответственно будущей подключаемой нагрузке;
- при монтаже электродвигателей, трансформаторов и других потребителей переменного тока – на значение cosϕ.
Снижение затрат на потери однозначно приводит к увеличению коэффициента полезного действия при совершении источником энергии работы на нагрузку.
Снижение влияния факторов, вызывающих потери мощности, увеличивает процент полезной мощности, необходимой для совершения работы. Это возможно при выявлении причин потерь и их устранении.
Видео
Источник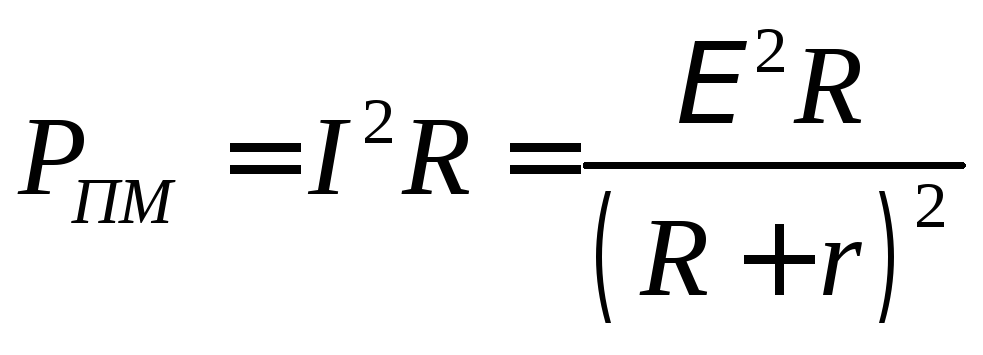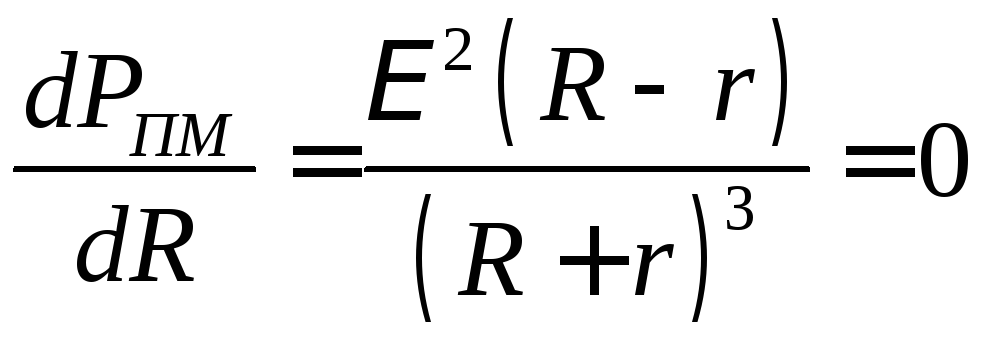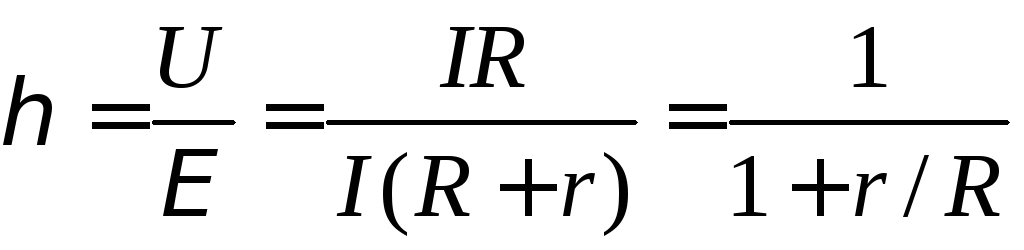